ВМ

УЧРЕЖДЕНИЕО БРАЗОВАН ИЯ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет заочного и дистанционного обучения

Специальность: ПОИТ

КОНТРОЛЬНАЯ РАБОТА

ПО ВЫСШЕЙ МАТЕМАТИКЕ № 1

Вариант № 4

Бартошко Геннадия Иосифовича

Группа 801021

Зачетная книжка 801021-04

Электронный адрес: ruletka-@mail.ru

№4. Даны четыре вектора (1,3,5), (0,2,0), (5,7,9), (0,4,16).

в некотором базисе. 1.Показать, что векторы , , образуют базис. 2. Найти координаты вектора в этом базисе

Решение:

1. Базисом в пространстве являются любые три некомпланарных вектора. Условием компланарности трех векторов является равенство их смешанного произведения нулю. Итак, находим

==1*2*9+5*0*7+5*3*0-5*2*5-1*0*7-3*0*9 = -32 ≠ 0

Векторы некомпланарны и образуют базис потому, что их смешанное произведение не равно 0

2. Составим систему уравнений в координатном виде

и найдем

-160 =64

Определитель найден выше и = -32

Имеем

Значит, .

==================================================================

№14 Даны координаты вершин пирамиды ,,,

Найти:

1) длину ребра А₁А₂;

2) угол между ребрами А₁А₂ и А₁А₄;

3) угол между ребром А₁А₄ и гранью А₁А₂А₃;

4) площадь грани А₁А₂А₃;

5) объём пирамиды;

6) уравнения прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

8) уравнения высоты, опущенной из вершины А₄ на грань А₁А₂А₃.

9)Сделать чертёж.

Решение.

1. Находим координаты векторов

=(5;2;0)

=(2;5;0)

=(1;2;4)

и длину ребра

2. Угол  между ребрами и вычисляется по формуле

cos =0.364698

3. Угол  между ребром и плоскостью - это угол между вектором и его ортогональной проекцией на грань .

Вектор перпендикулярен грани , что вытекает из определения векторного произведения векторов и

= i *-j *+k *=(0;0;21)

Отсюда

cos (90-)=sin===

= arcsin =arcsin 0.873=60,794

4. Площадь грани находим, используя геометрический смысл векторного произведения

S===10,5

5. Объем пирамиды численно равен одной шестой модуля смешанного произведения векторов , ,

V===14

6. Уравнение прямой в пространстве, проходящей через две заданные точки и, имеет вид

При и

уравнение прямой в каноническом виде

или уравнение прямой как линии пересечения двух плоскостей.

7.

Уравнение плоскости, проходящей через три заданные точки,,имеет вид

при ,,

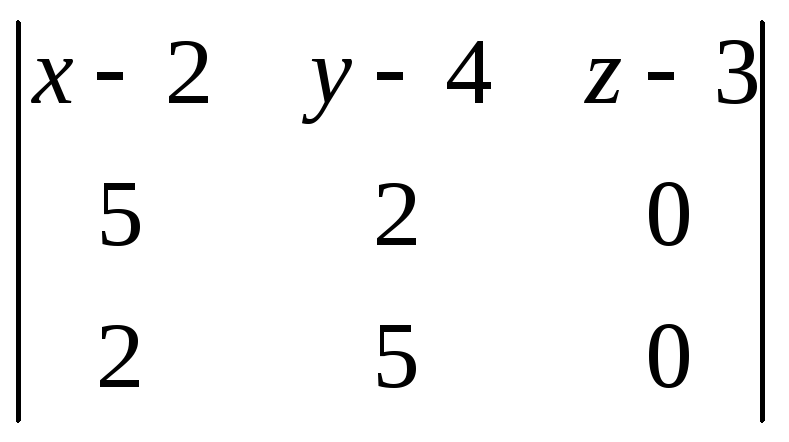=0 =0

(x-2)*2*0+(y-4)*2*0+5*5*(z-3)-2*2*(z-3)-5*0*(y-4)-5*0*(x-2)=0

21z-63=0 z-3=0

z-3=0 и есть уравнение плоскости проходящей через точки,,

8.Уравнение прямой высоты опущенной из точки на грань,,

где координаты точки , а (m,n,p) координаты

вектора параллельного искомой прямой, т.е. (0;0;21)

тогда уравнение данной прямой в каноническом виде будет

Выполним чертеж пирамиды с вершинами,,,

==================================================================

№24. Вычислить координаты центра окружности, описанной около треугольника с вершинами A(-1,1), B(2,-1), C(4,0)

Решение.

Центр окружности описанной около треугольника находится в точке пересечения серединных перпендикуляров сторон этого треугольника. Составим уравнение сторон

AB и BC.Учитывая что каноническое уравнение прямой имеет вид

Получаем уравнение прямой:

Для AB 2x+3y-1=0

Для BC x-2y-4=0

Координаты середины отрезка

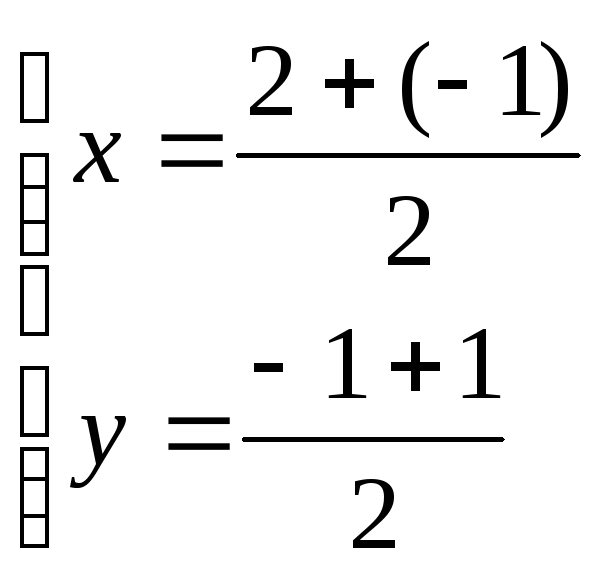
AB точка (0.5; 0)

BC точка (3;-0.5)

Уравнение прямой, проходящей через точку, и перпендикулярной данной прямой имеет вид

здесь координаты точки ,а угловой коэффицент при х

в уравнении прямой.

Для линии AB

2x+3y-1=0

перпендикуляр проходящий через точку(0.5; 0) будет выражен уравнением

4y=6x-3

Аналогично для линии BC

x-2y-4=0

перпендикуляр проходящий через точку(3;-0.5) будет выражен уравнением

2y+1=-4(x-3) 2y=-4x+11

Чтобы найти точку пересечения серединных перпендикуляров нужно решить систему уравнений

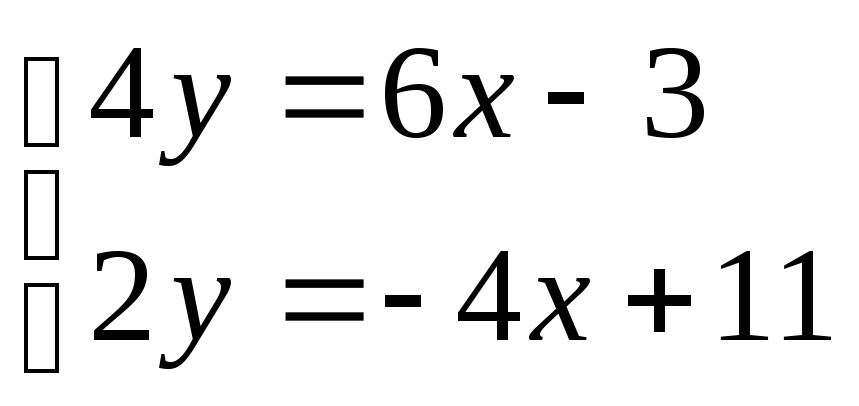
Отсюда получаем

x=; y=

О (1.7857;1.9286)

Это и есть координаты центра окружности, описанной около треугольника с вершинами A(-1,1), B(2,-1), C(4,0)

================================================================

№34 Построить на плоскости область решений системы линейных неравенств

Чтобы решить неравенство 6x-5y17 рассмотрим прямую 6x-5y=17 Она проходит через две точки (2;-1) и (1;-2,2). При x=0,y=0 неравенство 6x-5y17 является неверным. Следовательно, ему удовлетворяют все точки, лежащие ниже прямой 6x-5y=17 и на прямой.

Чтобы решить неравенство x+2y34 рассмотрим прямую x+2y=34 Она проходит через две точки (10;12) и (12;11) При x=0,y=0 неравенство x+2y34 является верным. Следовательно, ему удовлетворяют все точки, лежащие ниже прямой x+2y=34 и на прямой.

Чтобы решить неравенство -4x+9y17рассмотрим прямую -4x+9y=17 Она проходит через две точки (-2;1) и (-3;) При x=0,y=0 неравенство -4x+9y17 является неверным. Следовательно, ему удовлетворяют все точки, лежащие выше прямой x+2y=34 и на прямой.

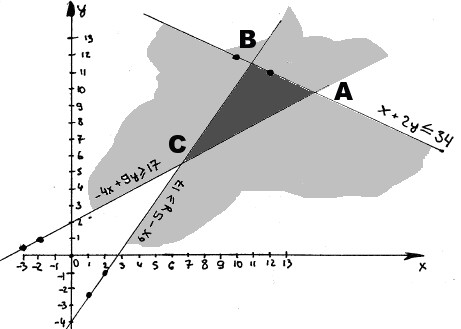
Находим точку А пересечения прямых -4x+9y=17 и x+2y=34 решая систему

A (16;9)

Находим точку B пересечения прямых 6x-5y=17и x+2y=34 решая систему

B (12;11)

Находим точку C пересечения прямых 6x-5y=17и -4x+9y=17 решая систему

C (7;5)

Данной системе неравенств удовлетворяют все точки внутри треугольника АВС и на его границе

№44. Составить уравнение линии, каждая точка которой находится вдвое ближе к точке A(1,0), чем к точке B(-2,0).

Сумма квадратов катетов равна квадрату гипотенузы. Исходя из этого можно составить систему уравнений.

при a=1-x b=-2-x

Подставляя в первое уравнение вместо его значение из второго уравнения получим:

Дополним уравнение до полного квадрата

получили уравнение окружности с радиусом 2 и центром в точке (2;0) это и есть искомое уравнение.