
курс 1, КОНТРОЛЬНАЯ 3, Вариант № 5
.docУЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
БЕЛАРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет заочного и дистанционного обучения
Специальность: Программное обеспечение информационных технологий
КОНТРОЛЬНАЯ РАБОТА
ПО ВЫСШЕЙ МАТЕМАТИКЕ № 1
Вариант № 5
ФИО
Группа
Зачетная книжка:
Электронный адрес:
Задача 85 Выделив в заданной функции полный квадрат, получить уравнение параболы и построить её график.
![]() .
.
Выделив полный квадрат в заданной функции, получим
![]() .
.
-
 - перенос графика функции
- перенос графика функции
 вдоль оси ОХ вправо на
вдоль оси ОХ вправо на
 ;
; -
 - сжатие относительно оси ОY
в 4 раза;
- сжатие относительно оси ОY
в 4 раза; -
 - перенос графика вверх вдоль оси ОУ на
21 ед.
- перенос графика вверх вдоль оси ОУ на
21 ед.
![]()

![]()
![]()
Задача
95 Задана функция
![]() на отрезке
на отрезке
![]() .
Требуется: 1) построить
график функции в полярной системе
координат по точкам, давая аргументу
.
Требуется: 1) построить
график функции в полярной системе
координат по точкам, давая аргументу
![]() значения через промежуток
значения через промежуток
![]() ;
2) найти каноническое
уравнение полученной линии в прямоугольной
декартовой системе координат, начало
которой совпадает с полюсом, а положительная
полуось абсцисс – с полярной осью, и по
уравнению определить тип линии.
;
2) найти каноническое
уравнение полученной линии в прямоугольной
декартовой системе координат, начало
которой совпадает с полюсом, а положительная
полуось абсцисс – с полярной осью, и по
уравнению определить тип линии.
![]() .
.
Составим таблицу значений:
|
|
0 |
|
|
|
|
|
|
|
|
r |
5 |
≈4,07 |
≈2,66 |
≈1,75 |
≈1,25 |
≈0,97 |
≈0,82 |
≈0,74 |
|
|
|
|
|
|
|
|
|
|
|
≈0,71 |
≈0,74 |
≈0,82 |
≈0,97 |
≈1,25 |
≈1,75 |
≈2,66 |
≈4,07 |
5 |
Для вычерчивания линии
проведем радиусы-векторы, соответствующие
углам
![]() ,
взятым с интервалом
,
взятым с интервалом
![]() .
На каждом из этих радиусов-векторов
откладываем отрезки, равные значению
r при соответствующем
значении
.
На каждом из этих радиусов-векторов
откладываем отрезки, равные значению
r при соответствующем
значении
![]() из таблицы. Соединяя точки, являющиеся
концами этих отрезков, получаем график
данной линии:
из таблицы. Соединяя точки, являющиеся
концами этих отрезков, получаем график
данной линии:
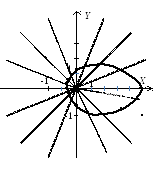
Подставляя
![]() и
и
![]() в уравнение заданной линии, получим
в уравнение заданной линии, получим

![]()
![]()
![]()
![]()
![]()



Полученное уравнение есть уравнение эллипса.
Задача 105 Найти указанные пределы, не пользуясь правилом Лопиталя.
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() .
.
1) ![]()
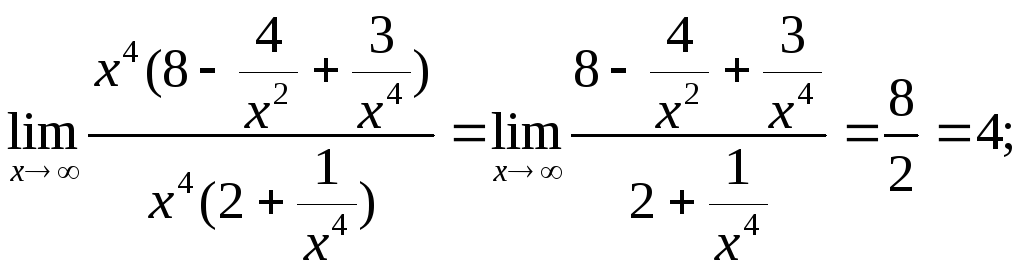
2) ![]()
![]()

3) ![]()
![]()

Задача 115 Найти указанные пределы, используя эквивалентные бесконечно малые функции.
1) ![]() ; 2)
; 2) ![]() .
.
1)  ;
;
2)  .
.
Задача
125 Задана функция
![]() различными аналитическими выражениями
для различных интервалов изменения
аргумента. Найти точки разрыва функции,
если они существуют, и установить их
тип. Сделать чертёж.
различными аналитическими выражениями
для различных интервалов изменения
аргумента. Найти точки разрыва функции,
если они существуют, и установить их
тип. Сделать чертёж.

Очевидно, что
![]() и
и
![]() являются точками, подозрительными на
разрыв.
являются точками, подозрительными на
разрыв.
Для первой части
функции
![]() .
Но на этом отрезке
.
Но на этом отрезке
![]()
Для третьей части
функции
![]() Но
эти функции не принадлежат к области
определения третьего отрезка.
Но
эти функции не принадлежат к области
определения третьего отрезка.
Значит область
определения
![]()
И в остальных точках функция непрерывна, так как на каждом из интервалов она определена и является элементарной.
Вычислим односторонние пределы.
![]()
![]() .
.
Поскольку найденные
пределы равны между собой и равны
![]() ,
в точке
,
в точке
![]() функция непрерывна.
функция непрерывна.
![]() ;
; ![]() .
.
Пределы равны между
собой, но в точке
![]() функция не определена. Значит
функция не определена. Значит
![]() является точкой устранимого разрыва.
является точкой устранимого разрыва.
![]() ;
;
![]()
Построим график с учетом проведенного исследования.




