Контрольная работа №2

Дифференциальное исчисление функций нескольких переменных

1)Найти область определения функции и изобразить эту область на плоскости.

Решение.

Функция будет определена при . При этом ясно, что начало координат не принадлежит области определения.

Изобразим эту область на плоскости:

2) Проверить, удовлетворяет ли указанному уравнению функция .

Решение.

Найдем частные производные первого порядка для данной функции:

;

.

Вычислим вторые частный производные:

;

;

.

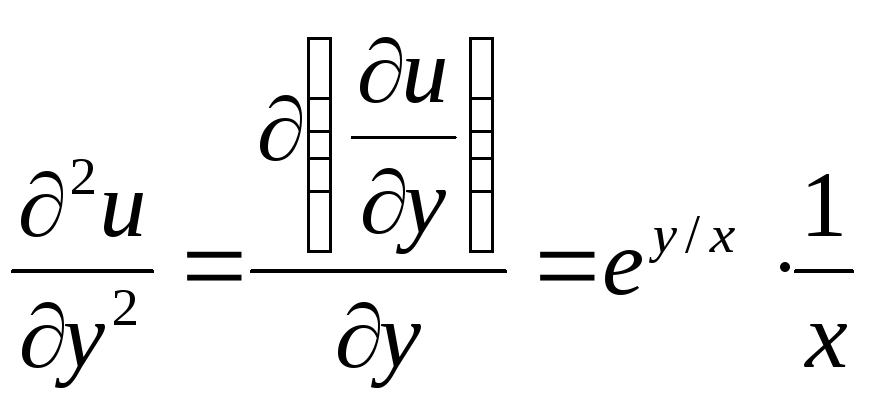Тогда

.

Допущена ошибка в условии задачи. Должно быть

3) Вычислить приближенное значение функции с помощью дифференциала.

Решение.

Рассмотрим функцию трех переменных и

положим x = 0; ; y = 0; ; z = 1; . Тогда выражение, которое надо вычислить, есть не что иное, как .

Воспользуемся приближенной формулой:

.

Вычислим .

Вычислим

.

; ;

; ;

; .

Тогда

.

Получим

.

4) Написать:

1) уравнение касательной плоскости и нормали к поверхности S, заданной уравнением z=f(x,y), в точке (x₀, y₀, f(x,y));

2) grad z в точке M₀(x₀,y₀);

3) производную функции z=f(x,y) в точке M₀(x₀,y₀) по направлению

вектора a.

Решение.

1) Уравнение касательной плоскости к поверхности S, заданной уравнением z=f(x,y), в точке (x₀, y₀, f(x₀,y₀)) имеет вид

.

Найдем частные производные в точке M₀(x₀,y₀).

; ;

;.

Вычислим значение функции .

Тогда искомое уравнение касательной плоскости:

Вектор нормали к поверхности в точке M₀(x₀,y₀) перпендикулярен к касательной плоскости в этой точке. Поэтому его координаты будут следующими:

.

2) Градиент функции в точке – это вектор, координаты которого равны частным производным функции в этой точке, т.е. .

3) Найдем производную функции z=f(x,y) в точке M₀(x₀,y₀) по направлению вектора

Производная функции z = f(x,y) в точке M₀(x₀,y₀) по направлению вектора a определяется как скалярное произведение вектора градиента в точке M₀(x₀,y₀) на вектор .

Поэтому, производная функции z = f(x,y) в точке M₀(x₀,y₀) по направлению вектора a будет равна

.

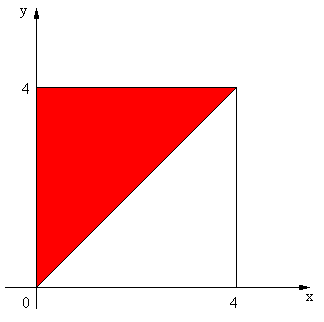
5)Найти наименьшее и наибольшее значения функции z=f(x,y) в указанной области. Сделать чертеж области.

в треугольнике .

Решение.

Проверим сначала наличие точек экстремума внутри области

D: . Для этого найдем частные производные

и приравняем их к нулю

.

Решением этой системы уравнений будет х = 1/2 и у = -3. Т.к. точка

(1/2, -3) не принадлежит области D, то внутри области D точек экстремума нет.

Найдем наибольшее и наименьшее значения функции на всех 3-х участках границы области D.

1) y = 4, : , . Значит 467/4, .

2) x = 0, : , - возрастает. Значит -4, .

3) , : ,

Значит ,

.

Из найденных значений функции выберем наибольшее и наименьшее.

Тогда наибольшим значением функции в замкнутой области D будет

, а наименьшим .

Сделаем чертеж.

6) Экспериментально получены пять значений функции y=f(x) при пяти значениях аргумента, которые записаны в табл. 1.

Таблица 1

x	1	2	3	4	5
y	y1	y2	y3	y4	y5

Методом наименьших квадратов найти функцию вида Y=ax+b, выражающую приближенно (аппроксимирующую) функцию y=f(x). Сделать чертеж, на котором в прямоугольной декартовой системе координат построить экспериментальные точки и график аппроксимирующей функции Y=ax+b.

Таблица 2

Задача	x	1	2	3	4	5
	Y	5,8	4,3	3,7	2,4	1,8

Решение.

По методу наименьших квадратов коэффициенты а и b линейной функции у = ах + b находятся по формулам:

;

.

Для данных нашей задачи n = 5;

15;

18;

44,1;

55.

Поэтому

;

.

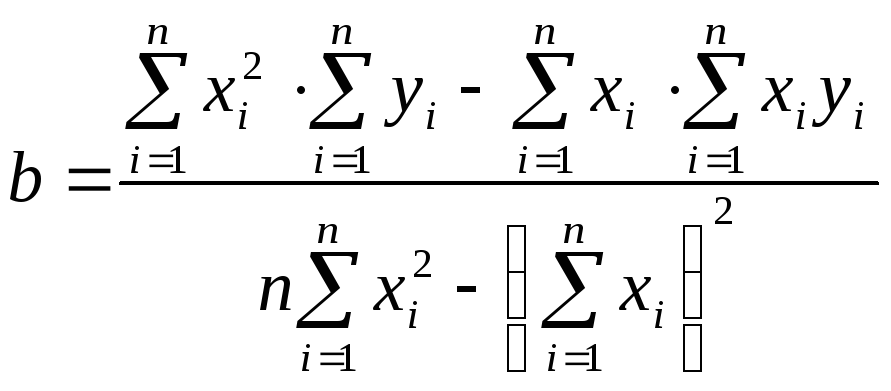
Уравнение линейной функции будет иметь вид:

у = -0,99х + 6,57.

Построим экспериментальные точки и график функции у = -0,99х + 6,57.

33