
Высшая математика часть 1. Контрольная работа №2. Вариант 4
.docУЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет заочного, вечернего и дистанционного обучения
Специальность: программное обеспечение
информационных технологий
КОНТРОЛЬНАЯ РАБОТА
ПО ВЫСШЕЙ МАТЕМАТИКЕ № 2
Вариант № 4
2. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Задание 54.
Доказать совместность данной системы линейных уравнений и решить ее двумя способами:
1) методом Гаусса;
2) средствами матричного исчисления.
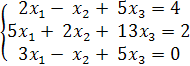
1) Решение методом Гаусса
При решении методом Гаусса используем расширенную матрицу:
![]() =
= 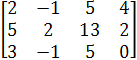
С помощью
элементарных преобразований приведём
![]() к треугольному виду:
к треугольному виду:
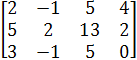
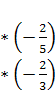 −>
−> 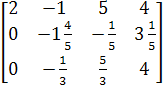
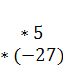
−> 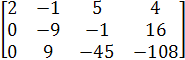 −>
−> 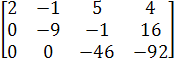
Таким образом, ранги основной и рассматриваемой матриц равны 3, и поэтому система имеет единственное решение, и она сводится к системе:
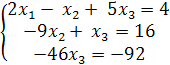 =>
=> 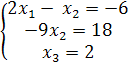 =>
=> 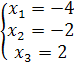
2) Решение средствами матричного исчисления
Найдём определитель системы:
Δ = 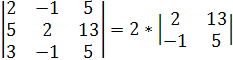 + 1 *
+ 1 * ![]() + 5 *
+ 5 * ![]() = 2 * (10+13) + 1 * (25−39) + 5(−5−6) = 46 – 14 – 55 = −23
= 2 * (10+13) + 1 * (25−39) + 5(−5−6) = 46 – 14 – 55 = −23
Так как
определитель матрицы отличен от нуля,
то решение найдём по формуле: X
= ![]() * B
* B
Найдём
обратную матрицу ![]() ,
для этого найдём алгебраические
дополнения
,
для этого найдём алгебраические
дополнения ![]() с учётом того, что
с учётом того, что ![]() имеет вид:
имеет вид:
![]() =
= ![]() *
* 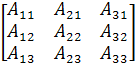
![]() =
= ![]() = 23
= 23 ![]() =
= ![]() = 0
= 0 ![]() =
= ![]() = −23
= −23
![]() =
= ![]() = 14
= 14 ![]() =
= ![]() = −5
= −5 ![]() =
= ![]() = −1
= −1
![]() =
= ![]() = −11
= −11 ![]() =
= ![]() = −1
= −1 ![]() =
= ![]() = 9
= 9
Проверим правильность вычисления обратной матрицы, исходя из её определения:
![]() * A
=
* A
= ![]() *
* 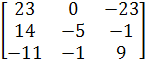 *
* 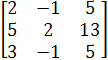 =
= ![]() *
* 
= ![]() *
* 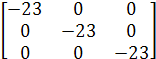 =
= 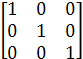 = E
= E
Значит, матричная система имеет вид:
![]() =
= ![]() *
* 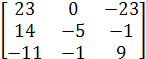 *
* ![]() =
= ![]() *
* 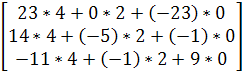 =
= ![]() *
*  =
= ![]()
Таким образом, ![]() = −4,
= −4, ![]() = −2,
= −2, ![]() = 2
= 2
Ответ: ![]() = −4,
= −4, ![]() = −2,
= −2, ![]() = 2
= 2
Задание 64.
Найти размерность и базис пространства решений однородной системы линейных уравнений.
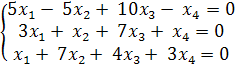
Найдём ранг основной матрицы системы с помощью элементарных преобразований:
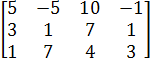 ~
~ 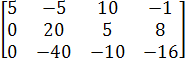 ~
~ 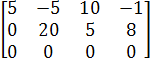
Таким образом, ![]() = 2
= 2
Так как ранг системы меньше числа неизвестных, то система имеет ненулевые решения. Размерность пространства решений этой системы: n – r = 4 – 2 = 2
Преобразованная система имеет вид:
![]() <=>
<=> ![]() <=>
<=>
![]() <=>
<=>
![]()
Эти формулы дают общее решение. В векторном виде его можно записать следующим образом:
![]() =
= ![]() =
= 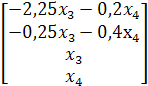 =
= ![]() *
* 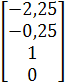 +
+ ![]()
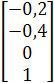
где ![]() ,
, ![]() − произвольные числа
− произвольные числа
Вектор−столбцы:
![]() =
= 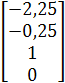 и
и ![]() =
= 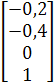
образуют базис пространства решений данной системы.
Задание 74.
Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее x1′′, x2′′, x3′′ через x1, x2, x3
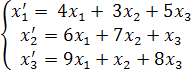
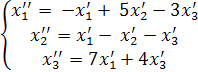
Решение
Первое линейное преобразование:
![]() = A
*
= A
* ![]() имеет матрицу А =
имеет матрицу А = 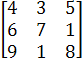
Второе:
![]() = B
*
= B
* ![]() имеет матрицу В =
имеет матрицу В = 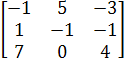 (*)
(*)
Тогда если в (*)
вместо В и ![]() поставить соответствующие матрицы,
получим:
поставить соответствующие матрицы,
получим:
C = B * A , то есть
C
= 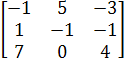 *
* 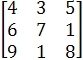 =
= 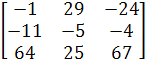
Поэтому искомое линейное преобразование имеет вид:
![]() =
= 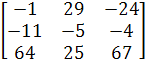 *
* ![]()
Задание 84.
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.
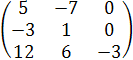
Составляем характеристическое уравнение матрицы:
![]() =
= 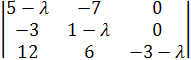 = 0
= 0
(5−λ)
* ![]() + 7 *
+ 7 * ![]() + 0 *
+ 0 * ![]() = 0
= 0
(5−λ) (1−λ) (−3−λ) + 7 (−3) (−3−λ) = 0 (**)
(5−6λ+![]() )
(−3−λ)
+ 63 + 21λ
= 0
)
(−3−λ)
+ 63 + 21λ
= 0
−15 +18λ
− 3![]() − 5λ
+ 6
− 5λ
+ 6![]() −
− ![]() + 63 + 21λ
= 0
+ 63 + 21λ
= 0
48 + 34λ
+ 3![]() −
− ![]() = 0 <=> (**) (λ
– 8) (λ
+ 2) (λ
+ 3) = 0
= 0 <=> (**) (λ
– 8) (λ
+ 2) (λ
+ 3) = 0
то есть ![]() = 8 ,
= 8 , ![]() = −3 ,
= −3 , ![]() = −2
= −2
При ![]() = 8 система имеет вид:
= 8 система имеет вид:
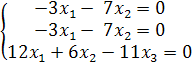 =>
=> ![]()
Выразим ![]() через
через ![]() :
:
4 * (−7![]() )
+ 6
)
+ 6![]() = 11
= 11![]()
−22![]() = 11
= 11![]() =>
=> ![]() = −0,5
= −0,5![]()
Выразим ![]() через
через ![]() :
:
12![]() + 6*(
+ 6*(![]() )
= 11
)
= 11![]()
![]()
84![]() − 18
− 18![]() = 77
= 77![]()
66![]() = 77
= 77![]() =>
=> ![]() = 1
= 1![]()
Таким образом,
числу ![]() = 8 соответствует собственный вектор:
= 8 соответствует собственный вектор:
![]() =
= ![]() =
= 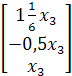 =
= ![]()
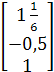
где ![]() − произвольное действительное число
− произвольное действительное число
Аналогично для
![]() = −3
= −3
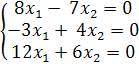 <=>
<=> ![]() =
= ![]() = 0
= 0
Таким образом,
числу ![]() = −3 соответствует собственный вектор
= −3 соответствует собственный вектор
![]() =
= ![]() =
= ![]() =
= ![]()
![]()
Наконец для ![]() = −2 решаем систему:
= −2 решаем систему:
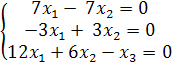 =>
=> ![]()
то есть вектор
![]() =
= ![]() =
=  =
= ![]()
![]()
Итак, матрица А
имеет три собственных значения: ![]() = 8 ,
= 8 , ![]() = −3 ,
= −3 , ![]() = −2. Соответствующие им собственные
векторы (с точностью до постоянного
множителя) равны:
= −2. Соответствующие им собственные
векторы (с точностью до постоянного
множителя) равны:
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
Задача 94.
Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм.
![]()
Левая часть
уравнения ![]() представляет собой квадратичную форму
с матрицей:
представляет собой квадратичную форму
с матрицей:
А = ![]()
Решаем характеристическое уравнение:
![]() = 0 , то есть
= 0 , то есть ![]() = 0
= 0
<=> (5−λ) (3−λ) = 8
![]() − 8λ
+ 7 = 0
− 8λ
+ 7 = 0
![]() = 1 ,
= 1 , ![]() = 7
= 7
Найдём собственные векторы из системы уравнений
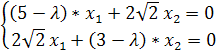 при
при ![]() = 1 ,
= 1 , ![]() = 7
= 7
Если ![]() = 1 , то:
= 1 , то:
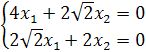 =>
=> ![]() =
= ![]()
Значит собственный
вектор ![]() =
= ![]() для
для ![]() = 1
= 1
Если ![]() = 7 , то:
= 7 , то:
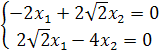 =>
=> ![]() =
= ![]()
значит собственный
вектор ![]() =
= ![]() для
для ![]() = 7
= 7
Нормируем собственные векторы, по правилу:
![]() =
= ![]() , получаем:
, получаем:
![]() =
=
![]()
![]() =
=
![]()
Составляем матрицу перехода от старого базиса к новому:
T
= 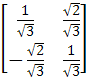
Выполняя преобразования:
![]() = T
= T
![]() =
= 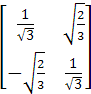 *
* ![]() =
= 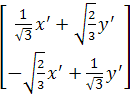 =>
=>
x
= ![]() +
+![]() , y
=
, y
= 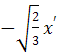 +
+![]()
Подставим полученные x и y в исходное уравнение и полученное уравнение упростим:
5  +
+ ![]()
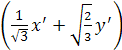
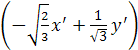 + 3
+ 3 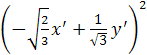 = 14
= 14
![]()
![]() +
+ ![]() + 2
+ 2![]() 2
2![]() +
+ ![]() = 14
= 14
![]() + 10
+ 10![]() + 10
+ 10![]() − 8
− 8![]() − 4
− 4![]() + 8
+ 8![]() + 6
+ 6![]() − 6
− 6![]() + 3
+ 3![]() = 42
= 42
![]() + 21
+ 21![]() = 42 =>
= 42 =>
![]() +
+ ![]() = 1 – каноническое уравнение эллипса
= 1 – каноническое уравнение эллипса
