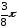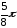ПОИТ Контрольная работа по высшей математике.№3
.docxУЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет непрерывного и дистанционного обучения
Специальность: программное обеспечение информационных технологий
КОНТРОЛЬНАЯ РАБОТА
ПО ВЫСШЕЙ МАТЕМАТИКЕ №3
3. ВВЕДЕНИЕ В АНАЛИЗ
106-110. Построить
график функции
 преобразованием графика функции
преобразованием графика функции
 .
.
-
Построим функцию y(x)=cos(x)
-
Сожмем у(х) к оси ординат в 2 раза. Получим функцию у1(х)=cos(2x)
-
Перенесем параллельно график на 1 единицу вправо вдоль оси абсцисс. Получим функцию у2(х)=cos(2x-1)
-
Растянем график функции у2(х) от оси абсцисс в 2 раза. Получим конечную функцию у3(х)=2cos(2x-1)

111-120. Дана функция
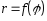 на отрезке
на отрезке
 .
Требуется: 1) построить график функции
в полярной системе координат по точкам,
давая
значения через промежуток /8,
начиная от =0;
2) найти уравнение полученной линии в
прямоугольной декартовой системе
координат, начало которой совпадает с
полюсом, а положительная полуось абсцисс
– с полярной осью, и по уравнению
определить, какая это будет линия.
.
Требуется: 1) построить график функции
в полярной системе координат по точкам,
давая
значения через промежуток /8,
начиная от =0;
2) найти уравнение полученной линии в
прямоугольной декартовой системе
координат, начало которой совпадает с
полюсом, а положительная полуось абсцисс
– с полярной осью, и по уравнению
определить, какая это будет линия.
120. 
1. Составим таблицу
|
|
0 |
|
|
|
|
|
|
|
|
|
r |
2 |
2.1 |
2.3 |
2.9 |
4 |
6.5 |
8 |
13.7 |
52.5 |
|
|
|
|
|
|
|
|
|
|
2π |
|
|
52.5 |
13.7 |
8 |
6.5 |
4 |
2.9 |
2.3 |
2.1 |
2 |
Из таблицы видно,
что при

 ;
Для вычерчивания линии проведем
радиусы-векторы, соответствующие углам
φ, взятым с интервалом
;
Для вычерчивания линии проведем
радиусы-векторы, соответствующие углам
φ, взятым с интервалом
 .
На каждом из этих радиусов-векторов
откладываем отрезки, равные значению
r
при соответствующем значении
.
На каждом из этих радиусов-векторов
откладываем отрезки, равные значению
r
при соответствующем значении
 из таблицы . Соединяя точки, являющиеся
концами этих отрезков, получаем график
данной линии:
из таблицы . Соединяя точки, являющиеся
концами этих отрезков, получаем график
данной линии:

2.
Подставляя
 и
и
 в уравнение заданной линии, получим
в уравнение заданной линии, получим
 Полученное
уравнение есть уравнение параболы с
ветвями, направленными вдоль оси абсцисс
в направлении отрицательной плоскости
и перенесенная вправо на 2 единицы.
Полученное
уравнение есть уравнение параболы с
ветвями, направленными вдоль оси абсцисс
в направлении отрицательной плоскости
и перенесенная вправо на 2 единицы.
121-130. Найти указанные пределы, не пользуясь правилом Лопиталя.
130.а) 
 б)
б)
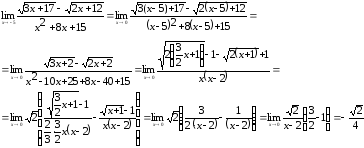
в)  г)
г)
-
Заданы функция
 и два значения аргумента
и два значения аргумента
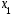 и
и
 .
Требуется: 1) установить, является ли
данная функция непрерывной или разрывной
для каждого из данных значений аргумента;
2) в случае разрыва функции найти ее
пределы при приближении к точке разрыва
слева и справа; 3) сделать схематический
чертеж.
.
Требуется: 1) установить, является ли
данная функция непрерывной или разрывной
для каждого из данных значений аргумента;
2) в случае разрыва функции найти ее
пределы при приближении к точке разрыва
слева и справа; 3) сделать схематический
чертеж.
140.
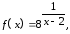


 -
функция в этой точке определена.
-
функция в этой точке определена.
 неопределенна,
т.к. в этой точке неопределенна функция
неопределенна,
т.к. в этой точке неопределенна функция
 .
Т.е. в этой точке разрыв. Определим тип
разрыва.
.
Т.е. в этой точке разрыв. Определим тип
разрыва.

Т.о. функция определена слева и неопределенна справа. Точка х=2 является неустранимым разрывом второго рода.
Сделаем схематический чертеж:

141-150. Задана функция
 различными аналитическими выражениями
для различных областей изменения
независимой переменной. Найти точки
разрыва функции, если они существуют.
Сделать чертеж.
различными аналитическими выражениями
для различных областей изменения
независимой переменной. Найти точки
разрыва функции, если они существуют.
Сделать чертеж.
150.

Функция
 непрерывна на
непрерывна на
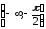 ,
функция
,
функция
 непрерывна на
непрерывна на
 ,
а
,
а
 непрерывна на
непрерывна на
 ,
значит
,
значит
 непрерывна на интервалах
непрерывна на интервалах
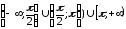 .
Остается исследовать точки
.
Остается исследовать точки
 и
и
 .
Находим правые и левые пределы функции
в этих точках.
.
Находим правые и левые пределы функции
в этих точках.

Т.е. в точке
 непрерывна.
непрерывна.

т.е.
 - неустранимый разрыв первого рода.
- неустранимый разрыв первого рода.
в
точке
 непрерывна.
непрерывна.
Сделаем ее чертеж