контр№6

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра программного обеспечения информационных технологий

Факультет НиДО

Специальность ПОИТ

Контрольная работа №6

по дисциплине «Высшая математика»

часть 2

Вариант № 3

Выполнил студент: ********

Группа *******

Зачетная книжка № ********

Минск 2011

Задания №263

Найти неопределенные интегралы (результаты в случаях “а” и “б” проверить дифференцированием).

263. а) 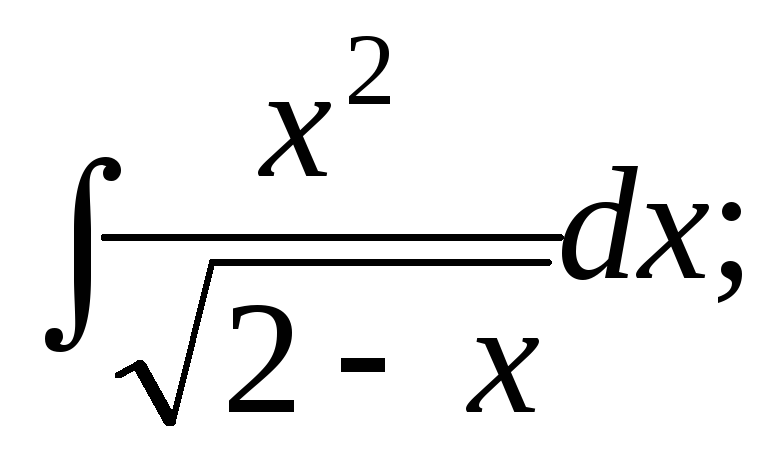б)

в) г) д)

а)

Решение

Применим подстановку . Отсюда

.

Подставив в интеграл, получим

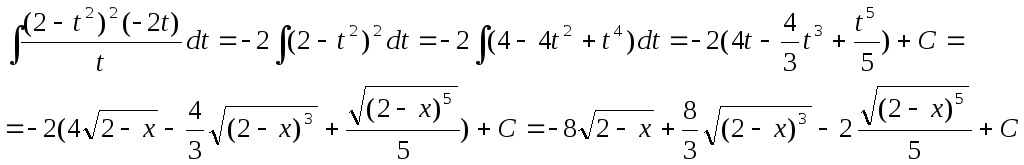
Проверка:

б)

Решение. Положим тогда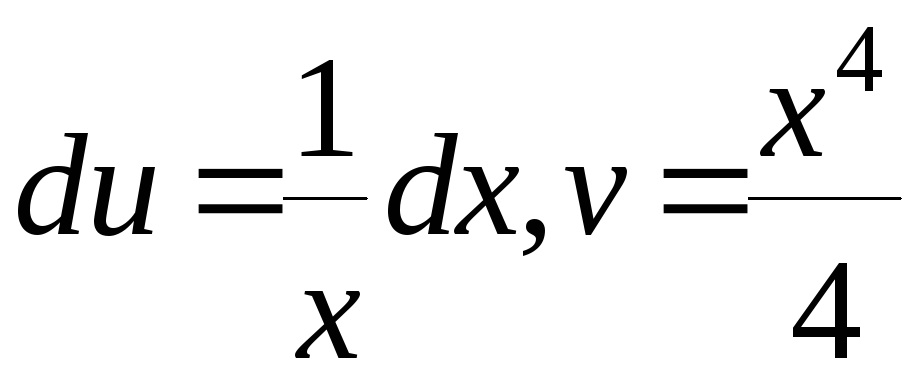 . Применим формулу интегрирования по частям:

.

Проверка:

в)

_{Решение:}

Учитывая, что , получаем разложение

Приводя к общему знаменателю, получим равенство числителей:

.

Приравнивая коэффициенты при одинаковых степенях , получаем

	A+C=0
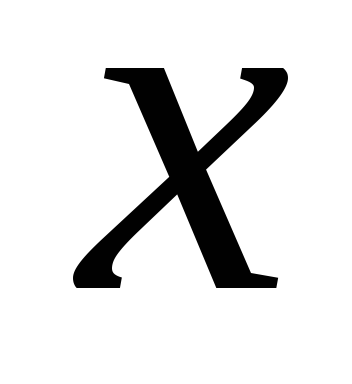
	A+B=0
	B+4C=1

Отсюда находим . Подставляя найденные коэффициенты в разложение и интегрируя его, получаем

_Г)

Применим подстановку . Отсюда

.

Подставив в интеграл, получим

Д)

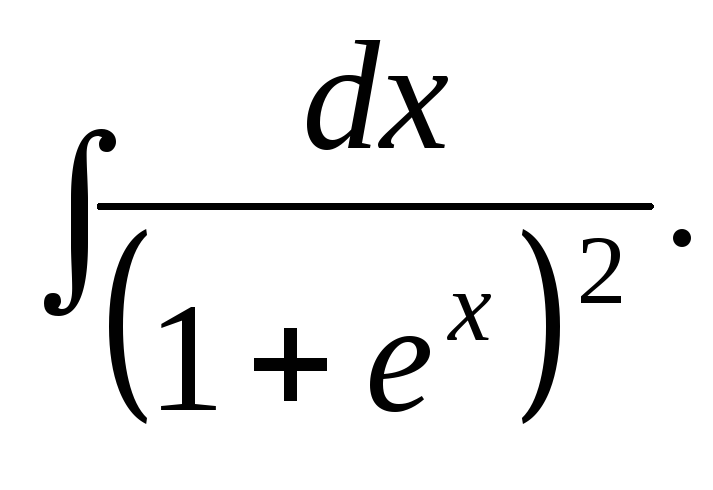
_{Решение:}

Применим подстановку . Отсюда

.

Подставив в интеграл, получим

получаем разложение

Приводя к общему знаменателю, получим равенство числителей:

.

Приравнивая коэффициенты при одинаковых степенях , получаем

	A+C=0
	B-А=0
	-B=1

Отсюда находим . Подставляя найденные коэффициенты в разложение и интегрируя его, получаем

Задание №273

Вычислить определенный интеграл. Окончательный результат представить в виде приближенного числа.

Решение:

Задание № 283

Вычислить несобственный интеграл или доказать его расходимость.

283. а) б)

А) Решение.

Подынтегральная функция не ограничена в окрестности точки . На любом же отрезке она интегрируема, так как является непрерывной функцией. Поэтому

Б)

Решение. Подынтегральная функция непрерывна и интегрируема на . По определению

Интеграл сходится.

Задание №293.

Вычислить площадь фигуры, ограниченной параболой и локоном Аньези

Решение. Найдем абсциссы точек пересечения параболы и прямой Решая уравнение , находим. Так как фигура ограничена сверху локоном Аньези, а снизу параболой, по известной формуле находим

Ответ:4,95(кв.ед)