КР 3 1курс 1 семестр 7 вариант

Введение в математический анализ

Задача 9. Требуется:

1) выполнить действия над комплексными числами, записав результат в показательной форме;

2) найти все корни уравнения.

1) ; 2) z⁴-30z²+289=0

Решение

1)

Комплексное число в показательной форме имеет вид:

Находим

2) z⁴-30z²+289=0

Для нахождение корней воспользуемся формулой:

Тогда

Тогда

Задача 10. Вычислить пределы функций, не пользуясь правилом Лопиталя.

 1) ; 2) ; 3) ;

 4) ; 5) ; 6) .

Решение

1)

2)

3)

4)

5)

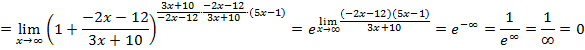
6)

Задача 11. Исследовать функцию f(x) на непрерывность и построить ее график. Определить характер точек разрыва.

f(x)=

Решение

Функция 1 непрерывна на , функция непрерывна на (0, 2] и функция x + 3 непрерывна на (2,+∞). Значит, функция f(x) непрерывна на интервалах . Остается исследовать точки х₁ = 0 и х₂ = 2.

Находим правые и левые пределы функции в этих точках:

Для х₁ = 0: f(0) = 1

Так как

, то функция в точке х₁ = 0 непрерывна.

Для х₂ = 2: f(2) = 4

Так как

, но существуют, значит, точка х = 2 точка разрыва 1-го рода

Сделаем схематический чертеж:

Задача 12. Исследовать функцию f(x) на непрерывность в указанных точках. Определить характер точек разрыва.

_{Решение}

Точка x₁ = -2 точка разрыва, так как в этой точке не определена функция

Функция в точке x₂ = -1 непрерывна

Находим пределы функции слева и справа:

Точка х = -2 является точкой разрыва 2-го рода.

Литература

1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1980.

2. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. – М.: Наука, 1970. Ч.1,2.

3. Высшая математика/Под ред. А.И. Яблонского. – Мн.: Выш. шк., 1993.

4. Мантуров О.В., Матвеев Н.М. Курс высшей математики. – М.: Высш. шк., 1986.

5. Жевняк Р.М. Карпук А. А. Высшая математика. Ч.1 – 4. – Мн.: Выш. шк., 1984-1988.

6. Шестаков А.А., Малышева И.А., Полозков Д.П. Курс высшей математики. – М.: Высш. шк., 1987.

7. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1965-1980.

8. Задачи и упражнения по математическому анализу для втузов/ Под ред. Б.П. Демидовича. – М.: Наука, 1964-1984.

9. Апатенок Р.Ф. и др. Элементы линейной алгебры и аналитической геометрии. – М.: Высш. шк., 1986.

10. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1,2 – М.: Высш. шк., 1980.

11. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для ВТУЗов. – М.: Наука, 1966.

12. Методические указания к контрольным работам по высшей математике для студентов-заочников. Ч.1,2,3. – Мн.: МРТИ, 1984.

13. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. Ч.1. – М.: Финансы и статистика, 1998.

14. Солодовников А.С., Бабайцев В.А., Браилов А.А., Шандра И.Г. Математика в экономике. Часть 2. – М.: Финансы и статистика, 1999.

15. Контрольные задания по общему курсу высшей математики /Ж.А.Черняк, А.А.Черняк, О.А.Феденя и др.; Под общей редакцией Ж.А.Черняк, А.А.Черняка. – СПб.: Питер, 2006. – 446 с.