
ВМ Кр№1
.pdf
Тема 1. Элементы линейной алгебры и аналитической геометрии
Вариант 9
9. Даны четыре вектора a ( a1 ; a2 ; a3 ), b ( b1 ;b2 ;b3 ), c ( c1 ;c2 ;c3 ) и d ( d1 ; d2 ; d3 ) в
некотором базисе. Показать, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
a (1;0;5), b (3;2;7), c (5;0;9), d (-4;2;-12).
Три вектора a , b , c линейно зависимы тогда и только тогда, когда они компланарны, т.е. определитель матрицы abc равен нулю.
abc = |
1 |
0 |
5 |
= 1*2*9+5*7*0+3*5*0-5*2*5-1*7*0-3*9*0 = -32 ≠ 0 |
3 |
2 |
7 |
||
|
5 |
0 |
9 |
|
Смешанное произведение векторов a , b , c отлично от нуля, следовательно, векторы
некомпланарны. Значит a , b , c являются линейно независимыми и образуют базис.
Если векторы a , |
|
, |
|
|
|
|
|
b |
c некомпланарны, то любой вектор d |
можно единственным образом |
|||||
разложить по ним. |
|
|
|
|
|
||
d = xa + yb + zc, где |
|
|
|
|
|
||
|
|
в базисе. |
|||||
x, y, z – координаты вектора d |
|||||||
-4 = 1*x + 3*y + 5*z |
-4 = x + 3y + 5z |
||||||
2 = 0*x + 2*y + 0*z |
2 = 2y |
||||||
-12 =5*x + 7*y + 9*z |
-12 = 5x + 7y + 9z |
||||||
Решаем систему уравнений
x + 3y + 5z = −42 y = 2
5x + 7 y + 9z = −12
находим y из второго уравнения: 2y = 2
y = 1
выражаем x из первого уравнения: x + 3y + 5z = - 4
x = -3y – 5z – 4
подставляем выражения для x и y в третье уравнение: 5x + 7y + 9z= -12
5(-3y – 5z – 4) + 7y + 9z= -12
2
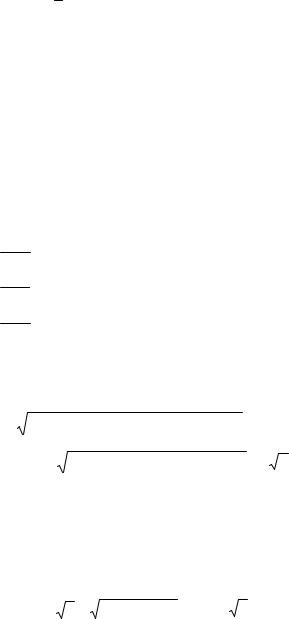
-15y – 25z – 20 +7y + 9z = -12 -16z = 8 + 8y
-16z = 16 z = -1
найдем x:
x = -3y – 5z – 4
x = -3*1 – 5*(-1) – 4 x = -3 + 5 – 4
x = -2
d = (-2)*a + 1*b +(-1)*c d = -2a + b – c
Вектор d в данном базисе имеет координаты x = -2, y = 1, z = -1
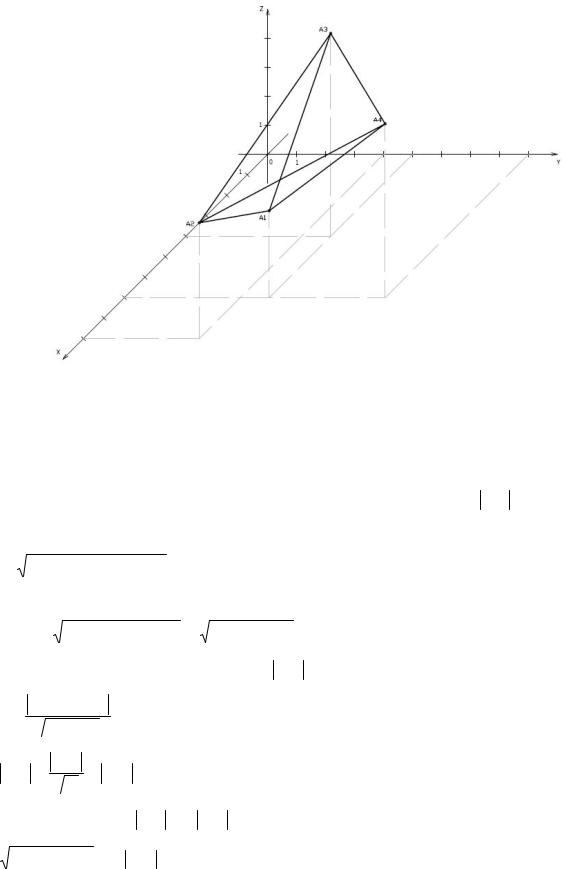
19. Даны координаты вершин пирамиды А1А2А3А4. Найти: 1) длину ребра А1А2; 2) угол между рёбрами А1А2 и А1А4; 3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объём пирамиды; 6) уравнения прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнения высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертёж.
А1 (7;5;3), А2 (9;4;4), А3 (4;5;7), А4 (7;9;6).
Находим координаты векторов А1А2 , А1А3 , А1А4
А1 А2 = (9-7;4-5;4-3) = (2;-1;1)
А1 А3 = (4-7;5-5;7-3) = (-3;0;4)
А1 А4 = (7-7;9-5;6-3) = (0;4;3)
1) находим длину ребра А1А2, которая равна расстоянию между точками А1 и А2 , по формуле
ρ= (х |
2 |
− х )2 |
+ ( у |
2 |
− у |
)2 |
+ (z |
2 |
− z )2 |
|||||
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|||
|
|
|
|
= (9 − 7)2 |
+ (4 − 5)2 + (4 − 3)2 = 6 |
|||||||||
|
А А |
|
||||||||||||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2) угол между рёбрами А1А2 и А1А4 вычисляем по формуле
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos φ = |
|
|
(А1 А2 , А1 А4 ) |
|
||||||||||
|
|
А А |
|
× |
|
А А |
|
|
|
|||||
|
|
|
|
|
||||||||||
|
|
|
1 |
2 |
|
|
|
1 |
4 |
|
|
|
||
cos φ = 2 × 0 + (−1) × 4 + 1× 3 = − |
1 |
|||||||||||||
5 6 |
||||||||||||||
|
|
6 × 02 + 42 + 32 |
||||||||||||
3
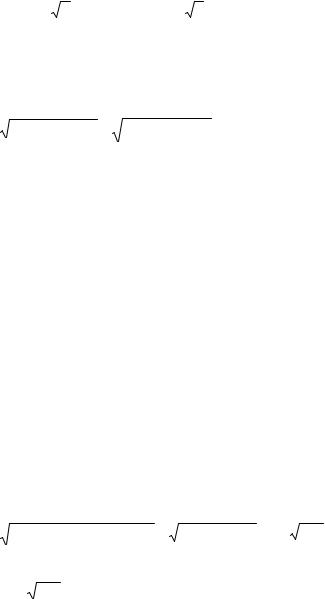
|
|
|
|
1 |
|
|
1 |
|||
φ = arccos |
|
− |
|
|
|
= π - arccos |
|
|
|
|
5 |
6 |
5 |
6 |
|||||||
3) угол между ребром А1А4 и гранью А1А2А3 определяем по формуле
sin θ = |
|
Ax1 + By1 + Cz1 |
|
|
|
, где |
|
|
|
|
|||||
|
|
|
|
|
|
||
A2 + B2 + C 2 × x 2 |
+ y 2 |
|
|||||
|
+ z 2 |
||||||
1 |
1 |
1 |
|
||||
x1, y1, z1 - координаты вектора,
А, В, С - коэффициенты уравнения плоскости Ax+By+Cz+D=0 Уравнение плоскости А1А2А3 записываем в виде
x − x1 |
y − y1 |
z − z1 |
|
x − 7 |
y − 5 z − 3 |
|
||||
|
|
|||||||||
x2 − x1 |
y2 − y1 |
z2 − z1 |
= 0 |
9 − 7 4 − 5 |
4 − 3 |
= 0 |
||||
x3 − x1 |
y3 − y1 |
z3 − z1 |
|
4 − 7 |
5 − 5 |
7 − 3 |
|
|||
x − 7 |
y − 5 |
z − 3 |
|
|
|
|
|
|
||
|
|
|
|
|
||||||
2 |
− 1 |
1 |
|
|
= 0 |
|
|
|
|
|
− 3 |
0 |
4 |
|
|
|
|
|
|
|
|
(x-7)*(-1)*4 + (-3)*1*(y-5) + (z-3)*2*0 - (z-3)*(-1)*(-3) - (x-7)*1*0 - 4*2*(y-5) = 0 - 4x - 11y - 3z + 92 = 0
|
|
|
|
|
|
|
|
|
|
|
|
А1 А4 = (0;4;3) |
|
|
|||||||
sin θ = |
|
|
(−4) × 0 + (−11) × 4 + (−3) × 3 |
|
|
= |
53 |
|||
|
|
|
||||||||
(−4)2 + (−11)2 + (−3)2 × 02 + 42 + 32 |
5 146 |
|||||||||
|
|
|
53 |
|
|
|
|
|
||
θ = arcsin |
|
|
|
|
||||||
5 146 |
|
|
||||||||
4) грань А1А2А3 является треугольником, площадь которого составляет половину площади параллелограмма, построенного на векторах А1А2 иА1А3
S A1A2A3 = |
1 |
|
× |
|
||
А А |
А А |
|||||
|
2 |
1 |
2 |
1 |
3 |
|
|
|
|
|
|
|
|
Координаты векторного произведения рассчитываем по формуле
|
|
|
|
|
|
|
|
|
|
y1 |
z1 |
|
|
|
|
x1 z1 |
|
|
|
x1 |
|
y1 |
|
|
|
||
А1 |
А2 |
× А1 А3 |
= |
|
× i − |
× j + |
× k |
||||||||||||||||||||
|
y2 |
z2 |
x2 z2 |
x2 |
|
y2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
= (2;-1;1) |
|
|
|
|
|
|
|
= (-3;0;4) |
|
|
|
|
|
|
|||||||||||
А1 |
А2 |
|
|
|
|
|
|
А1 А3 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
× |
|
|
= |
|
− 1 |
|
1 |
|
× i − |
|
|
2 |
1 |
|
× j + |
|
2 − 1 |
|
× k = -4i - 11j - 3k |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
А |
А |
2 |
А А |
3 |
|
||||||||||||||||||||||
1 |
|
1 |
|
|
|
0 |
|
4 |
|
|
|
|
− 3 |
4 |
|
|
|
|
− 3 0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
× |
|
|
3 |
= (-4; -11; -3) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
А1 |
А |
А1 |
А |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4

S A1A2A3 = |
1 |
× |
(−4)2 |
+ (−11)2 + (−3)2 = |
146 |
|
|
|
|
|
|
|||||||||||||
2 |
2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5) объём пирамиды вычисляем по формуле |
|
|
|
|
|
|||||||||||||||||||
V = 1 mod |
|
x2 − x1 |
y2 − y1 |
z2 − z1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x |
− x |
y |
3 |
− y |
z |
3 |
− z |
|
|
|
|
|
|
|
|
|
|
|
|||||
6 |
|
|
3 |
1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x4 |
− x1 |
y4 − y1 |
z4 − z1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
1 mod |
|
9 − 7 |
4 − 5 |
|
4 − 3 |
|
|
1 mod |
|
2 − 1 1 |
|
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
V A1A2A3A4 |
= |
|
|
4 − 7 |
5 − 5 |
|
7 − 3 |
|
= |
|
− 3 0 4 |
= |
mod (2*0*3 + 0*4*(-1) + |
|||||||||||
|
|
|
6 |
|
|
7 |
− 7 |
9 − |
5 |
|
6 − 3 |
|
|
6 |
|
|
0 4 3 |
|
6 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
+1*4*(-3) - 1*0*0 - 3*(-3)*(-1) - 2*4*4) = 536
6)уравнение прямой А1А2 как прямой проходящей через две точки записываем в виде
x − x1 |
= |
y − y1 |
= |
z − z1 |
|
x − 7 |
= |
y − 5 |
= |
z − 3 |
||||||||||
x |
2 |
− x |
|
|
y |
2 |
− y |
|
z |
2 |
− z |
|
9 − 7 |
|
4 − 5 4 − 3 |
|||||
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
||||
x − 7 |
= |
y − 5 |
= |
z − 3 |
|
- каноническое уравнение |
||||||||||||||
|
2 |
|
|
|
||||||||||||||||
|
|
|
− 1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
Обозначая равные отношения буквой t получаем уравнения вида
|
x=x0+a1t y=y0+a2t z=z0+a3t |
|
||||||
|
x − 7 |
= t |
|
y − 5 |
= t |
|
z − 3 |
= t |
2 |
|
− 1 |
1 |
|||||
|
|
|
|
|||||
x= 7+2t |
y= 5 - t |
|
z= 3 + t - параметрические уравнения |
|||||
7) уравнение плоскости А1А2А3 определено в п. 3 -4x - 11y - 3z + 92 = 0
8) каноническое уравнение прямой, проходящей через точку M0 (x0,y0,z0) и имеющей направляющий (любой ненулевой вектор параллельный прямой) вектор а = (а1,а2,а3), имеет вид
x − x0 |
= |
y − y0 |
= |
z − z0 |
||
а |
|
|
||||
|
а |
2 |
|
z |
3 |
|
1 |
|
|
|
|
||
Для искомых уравнений высоты точкой M0 является точка А4 (7;9;6), а за направляющий вектор а = (а1,а2,а3) может быть принят нормальный (перпендикулярный плоскости)
вектор n = (A, B, C). Для плоскости А1А2А3 n = (-4;-11;-3).
x − 7 |
= |
y − 9 |
= |
z − 6 |
|
каноническое уравнение высоты |
|||
− 4 |
− 11 |
|
− 3 |
||||||
|
|
|
|
|
|
||||
x − 7 |
= t |
y − 9 |
= t |
|
z − 6 |
= t |
|||
− 4 |
|
|
− 11 |
|
− 3 |
|
|||
x=7 - 4t |
|
y=9 - 11t |
z=6 - 3t параметрические уравнения высоты |
||||||
5
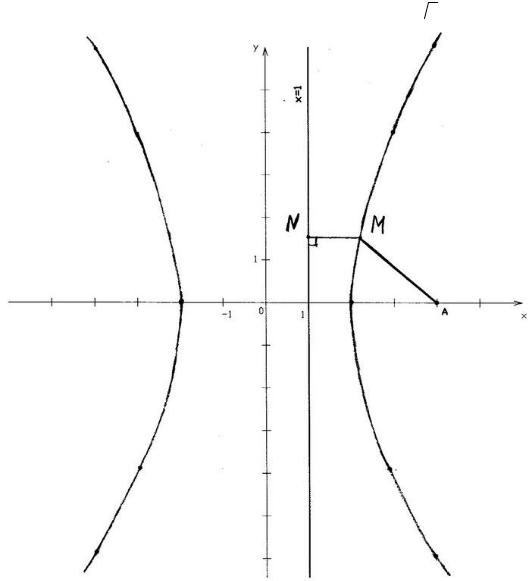
29. Составить уравнение линии, каждая точка которой отстоит от точки А (4;0) вдвое дальше, чем от прямой x = 1.
Пусть М (x,y) произвольная точка линии, N - основание перпендикуляра проведённого через точку М к прямой x = 1. Расстояние от точки А до точки М АМ определяем по формуле
ρ= (х |
2 |
− х )2 |
+ ( у |
2 |
− у |
)2 |
|||
|
|
|
|
1 |
|
1 |
|
||
А (4;0) , x = 1 |
|
|
|
|
|||||
|
АМ |
|
= (х− 4)2 + ( у − 0)2 = (x − 4)2 + y2 |
||||||
|
|
||||||||
Расстояние от точки М до прямой x = 1 NМ определяем по формуле
d = Ax + By + C
 A2 + B2
A2 + B2
NM = x − 1 = x − 1  12
12
По условию задачи AM = 2 NМ
(x − 4)2 + y2 = 2 x − 1
(х-4)2 + y2 = 4(x-1)2
x2 + y2 – 8x + 16 – 4x2 + 8x – 4 = 0 3x2 - y2 = 12
6
x2 |
− |
y2 |
= 1 |
|
4 |
12 |
|||
|
|
Полученное уравнение определяет гиперболу с полуосями a=2, b= 2 3
3
39. Доказать совместность данной системы линейных уравнений и решить её двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.
x1 − 2x2 + 3x3 = 62x1 + 3x2 − 4x3 = 203x1 − 2x2 − 5x3 = 6
Система, имеющая хотя бы одно решение, называется совместной.
1) для решения системы уравнений по методу Гаусса первое уравнение системы умножают на - а21/а11 и прибавляют ко второму; первое уравнение системы умножают на - а31/а11 и прибавляют к третьему.
Записываем расширенную матрицу
7
~ |
|
1 − 2 3 6 |
|
|
|
1 − 2 3 6 |
|
|
|
1 − 2 3 |
6 |
|
|
|
1 − 2 3 |
6 |
|
||
|
|
|
|
|
|
|
|
||||||||||||
|
2 3 − 4 20 |
|
→ |
|
0 7 − 10 8 |
|
→ |
|
0 |
7 − 10 |
8 |
|
→ |
|
0 |
0 14,5 |
29 |
|
|
А = |
|
|
|
|
|
|
|
|
|||||||||||
|
|
3 − 2 − 5 6 |
|
|
|
3 − 2 − 5 6 |
|
|
|
0 |
4 − 14 − 12 |
|
|
|
0 |
4 − 14 − 12 |
|
||
Вторая матрица получена из первой путём умножения первой строки на (-2) и прибавления ко второй строке. Третья матрица получена из второй путём умножения первой строки на (-3) и прибавления к третьей строке. Четвертая матрица получена из третьей путем умножения третьей строки на (-1,75) и сложения со второй строкой.
Записываем в виде системы уравнений
x1 − |
2x2 + 3x3 = 6 |
x1 − 2x2 + 6 = 6 |
|||
|
|
|
|
= 2 |
|
14,5x3 = 29 |
x3 |
||||
4x |
2 |
− 14x = −12 |
4x |
2 |
− 28 = −12 |
|
3 |
|
|
||
x1x2x3
=8
=4
=2
Система уравнений имеет решение x1=8, x2=4, x3=2, следовательно, является совместной.
|
|
|
1 − 2 |
3 |
|
|
|
|
|
|
|
||||
2) А = |
|
2 3 |
− 4 |
|
|
||
|
|
|
3 |
− 2 − 5 |
|
|
|
|
1 − 2 |
3 |
|
|
|
||
|
|
|
|
||||
∆= |
2 |
3 − 4 |
= 1*3*(-5) + 3*(-2)*(-4) + 3*2*(-2) - 3*3*3 - 1*(-2)*(-4) – (-5)*2*(-2) = -58 ≠ 0 |
||||
|
3 − 2 |
− 5 |
|
||||
Так как detA≠0, то матрица А имеет обратную матрицу и решение системы уравнений можно найти по формуле X=A-1*B или
|
x1 |
|
|
1 |
|
|
A11 A21 A31 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x |
2 |
= |
|
|
|
A |
|
|
|
|
A |
A |
|
× B |
|
|
|
, где B = |
20 |
|
|
, Aij |
|
алгебраические дополнения элементов аij |
||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
12 |
|
|
22 |
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
3 |
|
|
|
|
|
A |
|
|
|
|
A |
A |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
23 |
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
исходной матрицы А. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
А11= |
|
3 − 4 |
|
|
|
=-23, А12= - |
|
|
|
2 − 4 |
|
|
= -2, А13= |
|
2 3 |
|
=-13, А21= - |
|
− 2 3 |
|
= -16, А22= |
|
1 3 |
|
=-14, |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
− 2 − 5 |
|
|
|
|
|
|
3 |
− 5 |
|
|
|
3 − 2 |
|
|
− 2 − 5 |
|
|
3 − 5 |
|
||||||||||||||||||||||||||||||||||
А23 = - |
|
1 − 2 |
|
= -4, А31 = |
|
− 2 3 |
|
= -1, А32 = - |
|
1 3 |
|
= 10, А33 = |
|
1 − 2 |
|
= 7 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
3 − 2 |
|
|
|
|
3 − 4 |
|
|
2 − 4 |
|
|
2 |
3 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Матричное решение системы имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
|
|
1 |
|
− 23 |
− 16 |
− 1 |
|
6 |
|
|
|
|
1 |
|
− 464 |
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
= |
|
|
|
|
|
− 2 |
− 14 |
10 |
× |
|
20 |
|
= − |
|
|
− 232 |
|
= |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
− 58 |
58 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
x |
3 |
|
|
− 13 − 4 |
7 |
|
|
6 |
|
|
|
|
|
− 116 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Система уравнений имеет решение x1=8, x2=4, x3=2, следовательно, является совместной.
8
49. Найти размерность и базис пространства решений однородной системы линейных уравнений.
7x1 + 5x2 − 3x3 + x4 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3x1 + 2x2 − 3x3 + 2x4 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x + x |
2 |
+ 3x − 3x |
4 |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
7 5 − 3 |
1 |
|
|
|
7 5 − 3 1 |
|
|
|
7 5 − 3 1 |
|
|
|
7 |
5 − 3 1 |
|
|
||||
|
|
|
|
|
|
|
|
||||||||||||||
|
3 2 − 3 |
2 |
|
→ |
|
− 4 − 3 0 1 |
|
→ |
|
− 4 − 3 |
0 1 |
|
→ |
|
− 4 − 3 0 1 |
|
|
||||
|
1 1 3 − 3 |
|
|
|
1 1 3 − 3 |
|
|
|
8 6 |
0 − 2 |
|
|
|
0 |
0 0 0 |
|
|
||||
Вторая матрица получена из первой путём умножения первой строки на (-1) и прибавления ко второй строке. Третья матрица получена путем прибавления первой строки к третьей строке. Четвёртая матрица получена умножением второй строки на 2 и прибавлением к третьей строке.
7 5 |
= 7*(-3) - 5*(-4)= -1 ≠ 0 |
− 7 − 4 |
|
Ранг матрицы rA= 2, число неизвестных (число столбцов матрицы) n=4. Размерность пространства решений системы n-r = 4-2 = 2, следовательно, существует базис этого пространства, состоящий из двух векторов, через который выражается любое решение системы.
7x1 + 5x2 − 3x3 + x4 = 0 |
3x3 = 7x1 + 5x2 + x4 |
|
|
|
7x1 |
|
5x2 |
||||||
x3 |
= |
|
+ |
|
|
||||||||
3 |
3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
− 4x1 |
− 3x2 |
+ x4 |
= 0 |
x4 |
= 4x1 + 3x2 |
x |
4 |
= 4x |
+ 3x |
2 |
|||
|
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
|
|
|
|
= |
3 |
2 |
x1 + |
2 |
2 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x3 |
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
4 |
= |
4x |
|
+ 3x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Записываем общее решение в векторном виде |
||||||||||||||||||||||||||||||||
|
|
|
x1 |
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
X = |
= |
|
|
2 |
|
|
|
|
|
2 |
|
|
= |
x1 |
|
|
2 |
|
+ x2 |
|
|
|
2 |
|
|
|
|
||||
|
x |
|
3 |
x |
|
+ 2 |
|
x |
|
3 |
|
|
|
2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|||||||||
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x4 |
|
|
|
4x1 + 3x2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
3 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
Вектор-столбцы |
|
|
X1 |
|
= |
|
3 |
2 |
и |
|
X 2 |
= |
|
2 |
2 |
|
образуют базис пространства решений данной |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||
системы.
9

59. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.
5 |
9 |
7 |
0 |
3 − 2 |
|
0 |
2 − 1 |
|
Находим корни характеристического уравнения, которые являются собственными значениями матрицы
A − λE |
|
|
5 − λ |
9 |
7 |
|
|
|
|
|
|||||
|
= |
0 |
3 − λ − 2 |
|
=0 |
||
|
|||||||
|
0 |
2 |
− 1 − λ |
|
|
||
(5-λ)*(3-λ)*(-1-λ) + 0*9*(-2) + 0*2*7 - 0*7*(3-λ) - 0*9*(-1-λ) - 2*(-2)*(5-λ) = 0 (5-λ)*(3-λ)*(-1-λ) + 4*(5-λ) = 0 -λ3 + 7λ2 – 11λ + 5 = 0 (5-λ)*( λ2 – 2λ + 1) = 0 (5-λ)*(λ – 1) 2 = 0
5-λ = 0 |
λ – 1 = 0 |
λ1 = 5 |
λ2,3 = 1 (двукратный корень) |
Находим собственные векторы матрицы, подставляя корни характеристического уравнения в систему
(5 − λ )x1 + 9x2 + 7x3 = 0(3 − λ )x2 − 2x3 = 0
2x2 + (−1 − λ )x3 = 0
Для λ1 = 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9x2 + 7x3 = 0 |
x |
|
= − 7 x |
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
x1 |
|
|
|
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
9 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
= − x3 |
|
x2 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
X1 = |
|
x2 |
= |
0 |
= x1 |
0 |
|||||||||||||
− 2x2 − 2x3 = 0 |
x2 |
|
|
|
|
|
|
|
|
||||||||||||||||||
2x |
|
− 6x = 0 |
x |
|
= 3x |
|
x3 |
= 0 |
|
|
|
|
|
|
x |
|
|
0 |
|
|
|
0 |
|||||
|
2 |
3 |
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При х1=1 |
|
= (1;0;0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
X1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Для λ2 = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4x1 + 9x2 + 7x3 = 0 |
x1 = −4x3 |
|
|
|
x1 |
|
|
− 4x3 |
|
|
− 4 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
− 2x3 = 0 |
X 2 |
= |
x2 |
= |
x3 |
= x3 |
1 |
|
|
|
||||||||||||||||
2x2 |
|
|
|
|
|
|
|
||||||||||||||||||||
2x |
2 |
− 2x = 0 |
x2 = x3 |
|
|
|
|
x |
3 |
|
|
|
x |
3 |
|
|
|
1 |
|
|
|
|
|||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При х3=1 X 2 = (-4;1;1)
10

Для λ3 = 1
4x1 + 9x2 |
+ 7x3 |
= 0 |
x1 |
= −4x2 |
|
|
x1 |
|
− 4x2 |
|
− 4 |
|||||
|
|
|
|
|||||||||||||
|
|
− 2x3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= 0 |
|
X 3 |
= |
x2 |
= |
x2 |
= x2 |
1 |
|||||||
2x2 |
|
|
|
|||||||||||||
2x |
2 |
− 2x |
= 0 |
|
x3 |
= x2 |
|
|
x |
3 |
|
x |
2 |
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
При х2=1 |
|
= (-4;1;1) |
|
|
|
|
|
|
|
|
|
|
||||
X 3 |
|
|
|
|
|
|
|
|
|
|
||||||
69. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм.
6x2 + 2 |
|
|
10 xy + 3y2 = 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Запишем матрицу квадратичной формы 6x2 + 2 |
10 xy + 3y2 = 16 |
|||||||||||||||||||||||||||||||||||||||||||
а11=6, |
а12= а21= 10 , |
а22=3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
А = |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
10 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Находим собственные числа матрицы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
A − λE |
|
|
|
|
10 |
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
= |
6 − λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
10 |
|
3 − λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(6-λ)*(3-λ) - |
|
|
10 * |
10 |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
λ2 -9λ+8 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
D = 81 - 4*8 = 49 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
λ1= |
9 + 7 |
= 8 |
|
|
|
|
λ2= |
9 − 7 |
|
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Находим собственные векторы матрицы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6 − λ )x1 + 10x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
10x |
|
+ (3 − λ )x |
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для λ1=8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
− 2x + 10x |
2 |
= 0 |
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
10 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
x1= |
|
|
x2 |
X1 |
= |
|
1 |
|
= |
|
|
|
|
|
= x2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
2 |
|
|
2 |
2 |
|
|
|
||||||||||||||||||
10x |
|
− 5x |
|
= 0 |
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Для λ2=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
x1 |
|
|
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
5x1 + 10x2 = 0 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x2= − |
|
x1 |
|
X 2 |
= |
|
= |
|
|
|
|
|
|
|
= x1 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
10 |
|
|
|
|
10 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
10x |
|
+ 2x |
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
x |
|
|
− |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|||||
Находим представление квадратичной формы в другом базисе
11
