
КР №1,2 Вышка 7 вар
.doc7 вариант
№7
Даны
четыре вектора
![]() ,
,
![]() ,
,
![]() и
и
![]() в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы
![]() образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора
![]() в этом базисе.
в этом базисе.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Решение
 3*5*(-4)+4*0*2+(-5)*1*(-3)-2*5*(-3)-(-5)*4*(-4)-1*0*3=
3*5*(-4)+4*0*2+(-5)*1*(-3)-2*5*(-3)-(-5)*4*(-4)-1*0*3=
=-60+15+30-80=-95![]()
значит, векторы не компланарны и создают базис.

 8*5*(-4)+(-5)*1*17+(-16)*0*2-2*5*17-(-16)*(-5)*(-4)-8*0*1=-95
8*5*(-4)+(-5)*1*17+(-16)*0*2-2*5*17-(-16)*(-5)*(-4)-8*0*1=-95
 3*(-16)*(-4)+4*17*2+8*1*(-3)-(-3)*(-16)*2-17*1*3-4*8*(-4)=285
3*(-16)*(-4)+4*17*2+8*1*(-3)-(-3)*(-16)*2-17*1*3-4*8*(-4)=285
 3*5*17+(-5)*(-16)*(-3)+4*0*8-(-3)*5*8-4*(-5)*17-0*(-16)*3=
3*5*17+(-5)*(-16)*(-3)+4*0*8-(-3)*5*8-4*(-5)*17-0*(-16)*3=
=275-240+120+340=475
![]() ,
,
![]() ,
,
![]()
![]()
№17
Даны
координаты вершин пирамиды
![]() .
Найти:
.
Найти:
1)
длину ребра; 2) угол между ребрами
![]() и
и
![]() ;
3) угол между ребром
;
3) угол между ребром
![]() и гранью
и гранью
![]() ;
4) площадь грани
;
4) площадь грани
![]() ;
5) объем пирамиды; 6) уравнение прямой
;
5) объем пирамиды; 6) уравнение прямой
![]() ;
7) уравнение плоскости
;
7) уравнение плоскости
![]() ;
8) уравнение высоты, опущенной из вершины
;
8) уравнение высоты, опущенной из вершины
![]() на грань
на грань
![]() .
Сделать чертеж.
.
Сделать чертеж.
![]()
Решение
1)
Найдем координаты
![]() (3-5;8-5;4-4)=(-2;3;0)
(3-5;8-5;4-4)=(-2;3;0)
Найдем
длину
![]()
2)
Найдем угол
![]() :
:

![]() (5-5;8-5;2-4)=(0;3;-2)
(5-5;8-5;2-4)=(0;3;-2)
![]()
![]()
![]()
![]()
3)
найдем угол
![]() между
между
![]() и гранью
и гранью
![]() :
:
![]() -
угол между
-
угол между
![]() и его
ортогональной проекцией
и его
ортогональной проекцией![]() на плоскость
на плоскость
![]() ,
,
вектор
![]() -
произведение
-
произведение
![]() и
и
![]() ,
,
![]() ,
значит:
,
значит:

![]() (3-5;5-5;10-4)=(-2;0;6)
(3-5;5-5;10-4)=(-2;0;6)

![]() (18;12;6)
(18;12;6)
![]()
4)
Найдем площадь
![]() используя
геометрический смысл векторного
произведения:
используя
геометрический смысл векторного
произведения:
![]()
5)
Найдем объем пирамиды![]() :
:
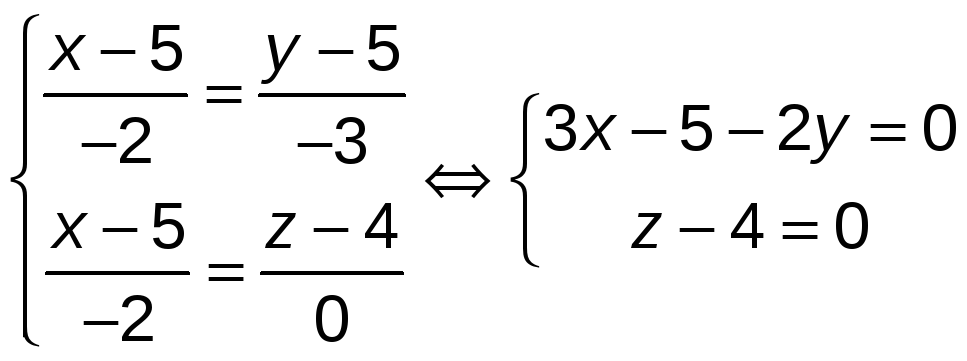

6) Уравнение прямой:
![]() ,
где
,
где
![]()

![]()
7) Уравнение плоскости:


8)Искомое
уравнение прямой получим из канонических
уравнений прямой![]() ,
где точка
,
где точка
![]() - точка лежащая на искомой прямой, m,n,p
– координаты вектора
- точка лежащая на искомой прямой, m,n,p
– координаты вектора
![]() ,
параллельного искомой прямой. В качестве
точки
,
параллельного искомой прямой. В качестве
точки
![]() возьмем
возьмем
![]() ,
а в качестве вектора
,
а в качестве вектора
![]() -
нормальный вектор плоскости
-
нормальный вектор плоскости
![]() -
вектор
-
вектор
![]() ,
то есть
,
то есть
![]() :
:
![]()
9) Сделаем чертеж:

№27
Составить уравнение линии, для каждой точки которой расстояние от точки А(0;1) вдвое меньше расстояния от прямой y=4.
Решение
Формула для нахождения расстояния от искомой линии до точки А будет вида:
![]() ,
,
до прямой y=4:
![]() ,
,
так
как
![]() должна быть в два раза больше
должна быть в два раза больше
![]() ,
то получим уравнение:
,
то получим уравнение:
![]() ,
возведем в квадрат обе части уравнения,
получаем
,
возведем в квадрат обе части уравнения,
получаем
![]() -
это каноническое уравнение гиперболы
с полуосями
-
это каноническое уравнение гиперболы
с полуосями
![]() и
2 и центром в начале координат.
и
2 и центром в начале координат.
№37
Доказать совместимость данной системы линейных уравнений и решить ее двумя способами: 1) методом Гауса; 2) средствами матричного исчисления:

1) Проверим совместимость данной системы:
 1*(-5)*(-1)+2*3*2+3*7*1-2*(-5)*1-3*2*(-1)-7*3*1=33
1*(-5)*(-1)+2*3*2+3*7*1-2*(-5)*1-3*2*(-1)-7*3*1=33![]() 0
0
Следовательно система совместима.
2)решим систему методом Гауса:
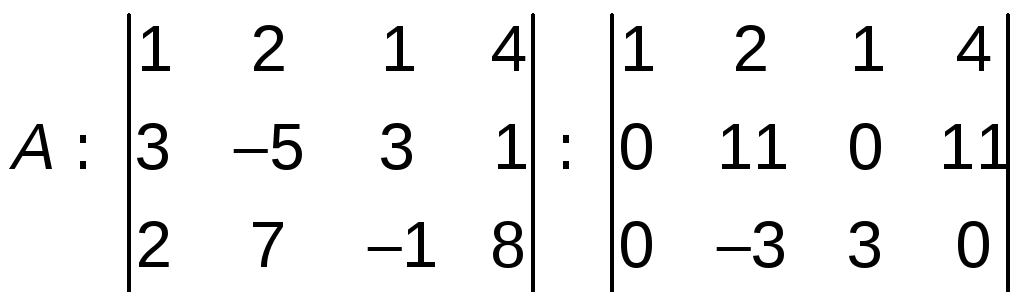 из 2-й строки вычтем 1-ю, умноженную на
3;
из 2-й строки вычтем 1-ю, умноженную на
3;
а из 3-й – 1-ю умноженную на 2, получим:

![]()
3) Решим систему средствами матричного исчисления:
так
как определитель
![]() ,
то находим решение по формуле
,
то находим решение по формуле
![]() или
или

![]() ,
,
![]()

Проверим правильность вычисления обратной матрицы:

 ,
следовательно, обратная матрица верно
вычислена.
,
следовательно, обратная матрица верно
вычислена.
Значит, матричное решение имеет вид:

Следовательно
![]() .
.
№47
Найти размерность и базис пространства решений однородной системы линейных уравнений.

Решение
Находим ранг основной матрицы системы с помощью элементарных преобразований:

Ранг матрицы равен 2
Так как ранг системы меньше числа неизвестных, то система имеет ненулевые решения. Размерность пространства решений этой системы n-r=2.
Преобразованная система, эквивалентная исходной, имеет вид:
 ,
,
Эти формулы дают общее решение. В векторном виде его можно записать следующим образом:
 ,
,
Где
![]() и
и
![]() - произвольные числа. Вектор-столбцы
- произвольные числа. Вектор-столбцы
![]() и
и

образуют базис пространства решений данной системы.
№57
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей:

Решение
Составим характеристическое уравнение матрицы:
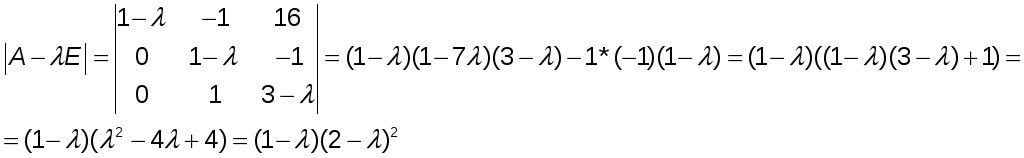 получим
что
получим
что
![]() и
и
![]() ,
,
При
![]() :
:

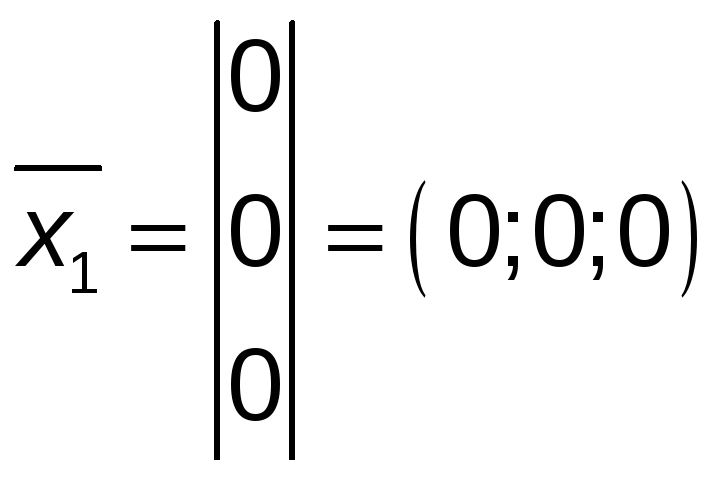 .
.
При
![]() :
:
 ,
,
 .
.
№67
Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм:
![]()
Решение
Левая часть уравнения представляет собой квадратичную форму с матрицей
 .
Решаем характеристическое уравнение
.
Решаем характеристическое уравнение
![]() ,
то есть
,
то есть

Получим
что
![]() и
и
![]() .
.
При
![]()
 ,
,

При
![]()
 ,
,
 .
.
Нормируем собственные векторы:

 ,
,

Составим матрицу перехода от старого базиса к новому:


![]() ,
,
![]()
![]()
![]()
Последнее уравнение есть каноническое уравнение элипса.
№77
Построить
график функции
![]() преобразованием графика функции
преобразованием графика функции
![]() :
:
![]()
Решение
Рассмотрим
данную функцию по частям относительно
![]() :
:
![]() -
график данной функции будет симметричен
графику
-
график данной функции будет симметричен
графику
![]() относительно оси ОХ;
относительно оси ОХ;
![]() -
график данной функции будет иметь
вершины в точках
-
график данной функции будет иметь
вершины в точках
![]() и
и
![]() ;
;
![]() -
период данной функции будет
-
период данной функции будет
![]() ;
;
![]() -
график данной функции будет смещен
влево на
-
график данной функции будет смещен
влево на
![]() .
.
Собирая воедино все выше рассмотренные отличия данной функции получим:
![]() -
график данной функции будет симметричен
графику
-
график данной функции будет симметричен
графику
![]() относительно оси ОХ, будет иметь вершины
в точках
относительно оси ОХ, будет иметь вершины
в точках
![]() и
и
![]() ,
период данной функции будет
,
период данной функции будет
![]() ,
график данной функции будет смещен
влево на
,
график данной функции будет смещен
влево на
![]() .
.

№87
Данная
функция
![]() на отрезке
на отрезке
![]() .
Требуется : 1) построить график функции
в полярной системе координат по точкам,
давая значения
.
Требуется : 1) построить график функции
в полярной системе координат по точкам,
давая значения
![]() через промежутки
через промежутки
![]() ,
начиная от
,
начиная от
![]() ;
2)Найти уравнение полученной линии в
прямоугольной декартовой системе
координат, начало которой совпадает с
полюсом, а положительная полуось – с
полярной осью, и по уравнению определить,
какая это будет линия.
;
2)Найти уравнение полученной линии в
прямоугольной декартовой системе
координат, начало которой совпадает с
полюсом, а положительная полуось – с
полярной осью, и по уравнению определить,
какая это будет линия.
Решение
![]()
Составим таблицу.


Из
таблицы видно, что при
![]() .
.
Для
построения линии проведем радиус-векторы,
соответствующие углам
![]() ,
взятым с интервалам
,
взятым с интервалам
![]() .
.
На
каждом из этих радиус-векторов откладываем
отрезки, равные значению
![]() при соответствующем значении
при соответствующем значении
![]() из таблицы. Соединяя точки, являющиеся
концами этих отрезков, получаем график
данной линии;
из таблицы. Соединяя точки, являющиеся
концами этих отрезков, получаем график
данной линии;

2)
Подставляя
![]() и
и
![]() в уравнение заданной линии, получаем
в уравнение заданной линии, получаем

![]()
Полученное
уравнение есть уравнение параболы с
вершиной А(0;2.5), ветви параболы направлены
вниз.![]()
№97
Найти указанные пределы, не пользуясь правилом Лопиталя:
![]()
![]()
![]()
![]()
![]()
Решение
а)
![]() ,
подстановка предельного значения
аргумента приводит к неопределенности
,
подстановка предельного значения
аргумента приводит к неопределенности
![]() .
Разделим числитель и знаменатель на
.
Разделим числитель и знаменатель на
![]() :
:
 ,
так как
,
так как
![]() ,
то дроби – бесконечно малые числа, ими
можно пренебречь.
,
то дроби – бесконечно малые числа, ими
можно пренебречь.
б)
![]() ,
подстановка предельного значения
аргумента приводит к неопределенности
,
подстановка предельного значения
аргумента приводит к неопределенности
![]() .
Умножим числитель и знаменатель на
.
Умножим числитель и знаменатель на
![]() :
:
![]() .
.
в)
![]() ,
подстановка предельного значения
аргумента приводит к неопределенности
,
подстановка предельного значения
аргумента приводит к неопределенности
![]() .
.
![]() ,
пусть t=3x:
,
пусть t=3x:
 .
.
г)
![]()
![]()
Разделим
числитель и знаменатель на
![]() , так как
, так как
![]() ,
то дроби – бесконечно малые числа, ими
можно пренебречь:
,
то дроби – бесконечно малые числа, ими
можно пренебречь:
 .
.
№107
Заданы
функция
![]() и два значения аргумента
и два значения аргумента
![]() и
и
![]() .
Требуется 1) установить, является ли
данная функция непрерывной или разрывной
для каждого из данных значений аргумента;
2) в случае разрыва функции найти ее
пределы при приближении к точке разрыва
слева и справа; 3) сделать схематический
чертеж.
.
Требуется 1) установить, является ли
данная функция непрерывной или разрывной
для каждого из данных значений аргумента;
2) в случае разрыва функции найти ее
пределы при приближении к точке разрыва
слева и справа; 3) сделать схематический
чертеж.
![]() ,
,
![]() ,
,
![]()
Решение
1)При
![]() ,
,
![]() - функция непрерывна;
- функция непрерывна;
При
![]() ,
,
![]() - функция неопределенна.
- функция неопределенна.
2) при приближении к точке разрыва справа:
![]() ;
;
при приближении к точке разрыва слева:
![]()
3)

№117
Задана
функция
![]() различными аналитическими выражениями
для различных областей изменения
независимой переменной. Найти точки
разрыва функции, если они существуют.
Сделать чертеж.
различными аналитическими выражениями
для различных областей изменения
независимой переменной. Найти точки
разрыва функции, если они существуют.
Сделать чертеж.

Решение
Функция
![]() непрерывна на
непрерывна на
![]() ;
;
Функция
х непрерывна на
![]() ;
;
Функция
0 непрерывна на
![]() ,
,
значит
![]() непрерывна на интервалах
непрерывна на интервалах
![]() .
.
Исследуем точки x=0 и x=2:
![]()
![]() -
функция непрерывна;
-
функция непрерывна;
![]()
![]() -
точка разрыва.
-
точка разрыва.
Видим, что односторонние пределы функции в точке х=2 существуют, но не равны между собой. Следовательно эта точка является точкой разрыва первого рода.

