математика кр2вариант 8

учреждения образования

белорусский государственный университет

информатики и радиоэлектроники

факультет заочного и дистанционного обучения

программное обеспечение информационных технологий

контрольная работа №2

по высшей математике

вариант №8

1. Доказать совместность данной системы линейных уравнений и решить её тремя методами: 1) по формулам Крамера; 2) методом Гаусса; 3) средствами матричного исчисления (с помощью обратной матрицы).

Решение:

1)

2) ====

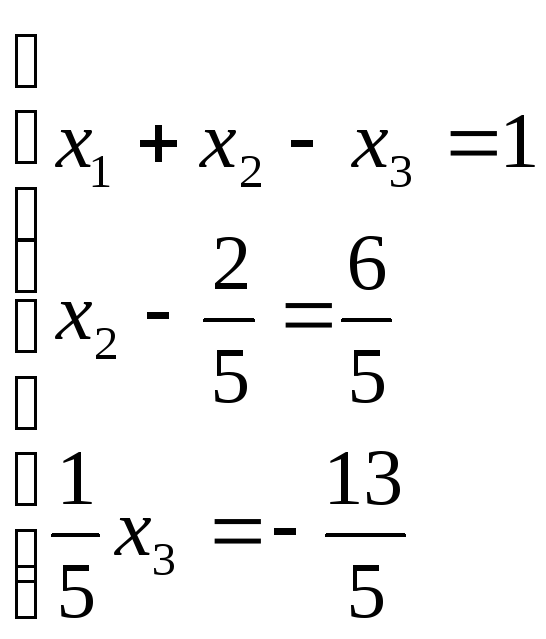Ответ: ; ;

3)

2. Найти общее решение системы линейных уравнений

Решение:

Выпишем расширенную матрицу системы и преобразуем её.

вычитаем из 2-й и 3-й строк 1-ю,тумноженную на 2 и 1

отбросим 3-ю строку, т.к. она совпадает со 2-й строкой

прибавим к 1-й строке 2-ю, умноженную на 3

Таким образом, путем элементарных преобразований мы привели расширенную матрицу системы к “диагональному” виду. Соответствующая система имеет вид:

Так как полученная система содержит 5 переменных и состоит из двух уравнений, то исходная система имеет бесконечное множество решений. 5-2=3 переменные нужно положить свободным.

Пусть:

Тогда

-общее решение.

Ответ:

3. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

Решение:

-собственные значения

Найдем собственный вектор с собственным значением

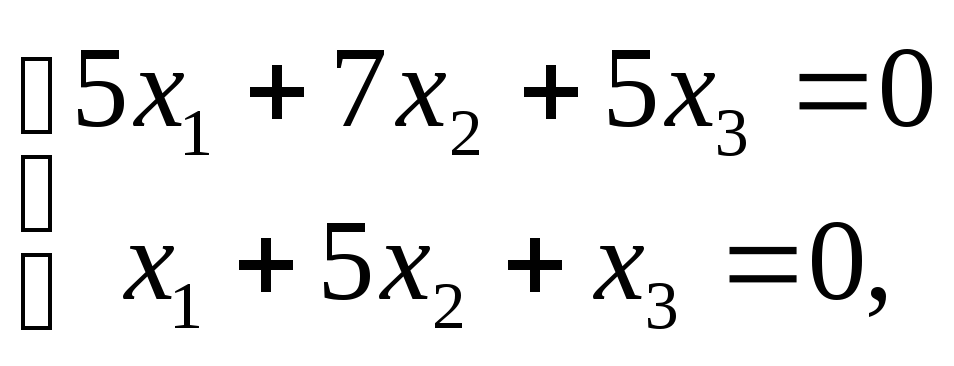
Собственный вектор с собственным значением

Для получим систему:

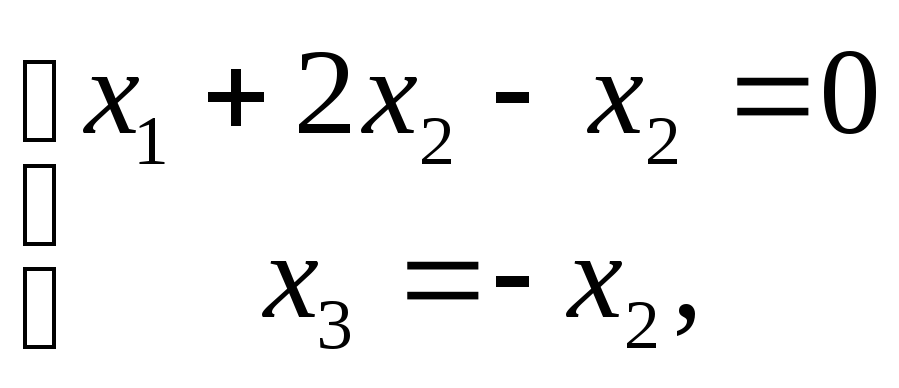
Для получим систему:

4. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка и построить её в декартовой системе координат

Решение:

Матрица А, составлена из коэффициентов при старших членах и её характеристическое уравнение:

Находим собственные векторы:

Для имеем систему:

для имеем систему:

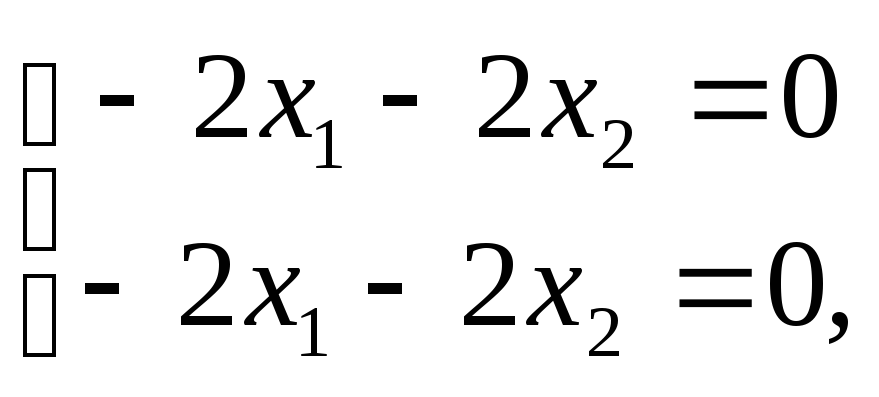
Совершим преобразование координат

(1)

В соответствии с формулой члены второй степени

преобразуются следующим образом:

Подставляя выражения для и из формулы (1) в оставшиеся члены уравнения, получим:

Исходная уравнение примет вид:

(2)

Совместим преобразование параллельного переноса по формулам:

Уравнение (2) перепишется в виде:

- пара пересекающих прямых.

Найдем точку, в которой находятся начало системы . Т.к. для этой точки то

Подставим точку относительно старой системы

Отложив из этой точки векторы , и направить по ним координаты оси построим пару пересекающихся прямых в новой системе