
Контрольная работа №3-4 Высшая математика 5 вариант
.doc3.Дифференциальное исчисление
125. Найти производную
![]() данных функций:
данных функций:
а)
![]()
![]()
![]()
б)
![]()
![]()
в)
![]()
![]()
г)
![]()
Прологарифмируем
обе части уравнения
![]() и преобразуем равенство
и преобразуем равенство
![]() Прологарифмируем обе части равенства
Прологарифмируем обе части равенства

![]()
д)![]() Дифференцируем обе части равенства,
учитывая, что у
есть функция от х,
получим
Дифференцируем обе части равенства,
учитывая, что у
есть функция от х,
получим
![]() или
или
![]()
![]()
135. Найти
![]() и
и
![]()
a) у= ln ctg 4x
![]()
![]()
б)
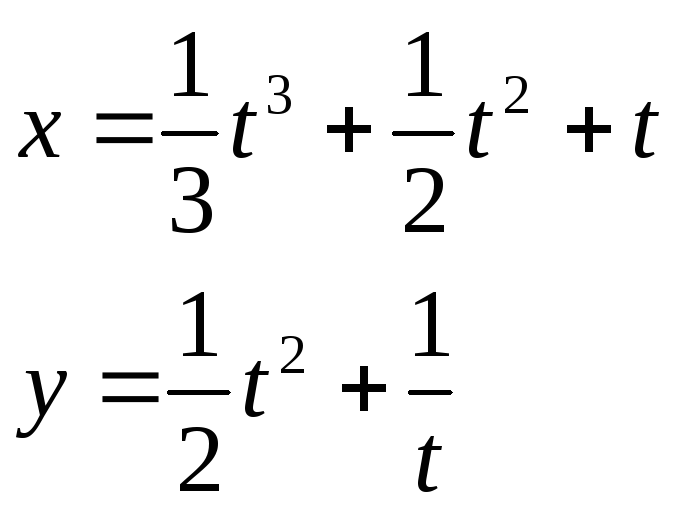
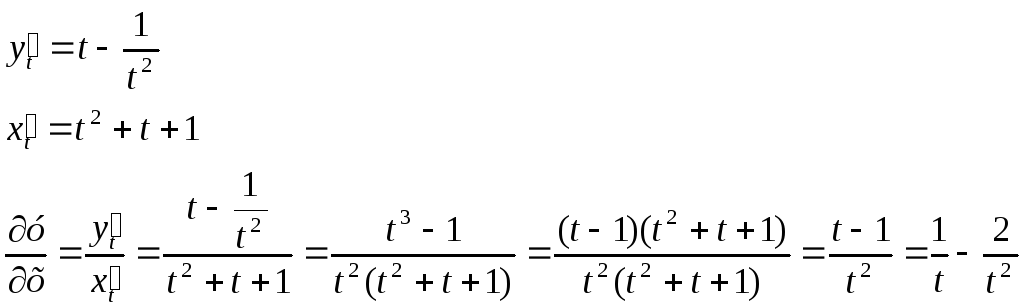
Получаем
![]()
Находим

145. Сопротивление балки прямоугольного сечения на изгиб пропорционально произведению ширины этого сечения и квадрата высоты. Каковы должны быть размеры сечения балки, вырезанной из круглого бревна диаметром d, чтобы ее сопротивление на изгиб было наибольшим?
П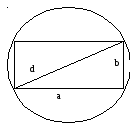 усть
стороны прямоугольника, диагональ
которого равна d,
равна а и b.
Сопротивление равно
усть
стороны прямоугольника, диагональ
которого равна d,
равна а и b.
Сопротивление равно
![]() .
Из прямоугольного треугольника выразим
сторону а:
.
Из прямоугольного треугольника выразим
сторону а:
![]()
Сопротивление тогда равно
![]() .
Заметим, что b
может изменяться от 0 до ∞. Найдём
производную
.
Заметим, что b
может изменяться от 0 до ∞. Найдём
производную
 .
Решим уравнение
.
Решим уравнение
![]() –критические точки. Первая точка не
подходит по условию. Исследуем на
экстремум вторую точку. Найдём вторую
производную :
–критические точки. Первая точка не
подходит по условию. Исследуем на
экстремум вторую точку. Найдём вторую
производную :
 .
Так как при
.
Так как при
![]() выполняется условие
выполняется условие
![]() ,
то в этой точке максимум функции. Значит,
высота прямоугольника будет равна
,
то в этой точке максимум функции. Значит,
высота прямоугольника будет равна
![]() ,
а ширина
,
а ширина
![]() .
Тогда сопротивление на изгиб будет
наибольшим.
.
Тогда сопротивление на изгиб будет
наибольшим.
155. Провести полное исследование функции и построить ее график
![]()
1) Область определения
D(y)=![]()
2) Т.к. область определения не симметрична относительно начала координат и
![]() ,
то функция является четной.
,
то функция является четной.
3) Точки пресечения с осями координат
с Ох : у=0 х=0 т.(0; 0)
с Оу: х=0 у= 0 т.(0; 0)
4) Асимптоты
Т.к. точки разрыва -1;1, то находим пределы

Прямые х=-1 х=1 вертикальные асимптоты
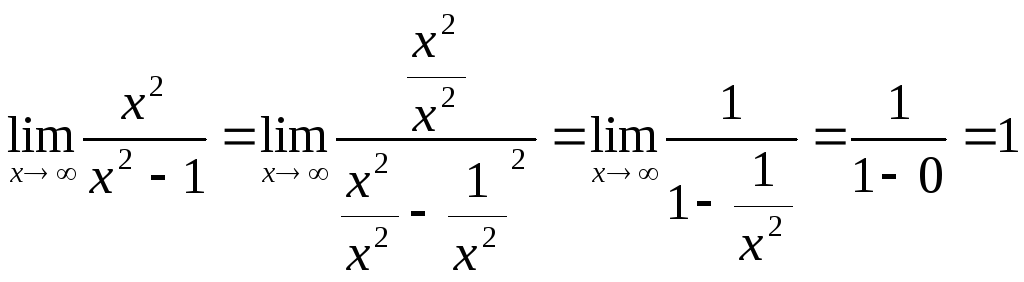
Это значит, что у=1 горизонтальная асимптота
Проверим, существует ли наклонная асимптота
 ,
т.е. наклонной асимптоты нет.
,
т.е. наклонной асимптоты нет.
5)Промежутки возрастания, убывания, точки экстремума
![]()
![]() =0
х=0 - критическая точка
=0
х=0 - критическая точка
- +
у
1
0
у
-1
max

точка разрыва
точка разрыва
Функция возрастает на промежутках (-∞;-1), (-1; 0) и убывает на промежутках (0;1), (1; +∞) и (-1;0), при х=0 получаем точку максимума у(0)= 0
6) Выпуклость, вогнутость функции
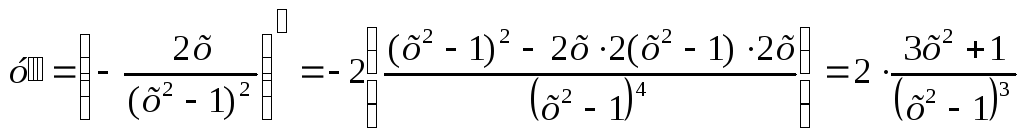
Решаем уравнение
![]() =0.
Это уравнение не имеет решений, след
точек перегиба нет
=0.
Это уравнение не имеет решений, след
точек перегиба нет
По результатам исследования функции строим график.
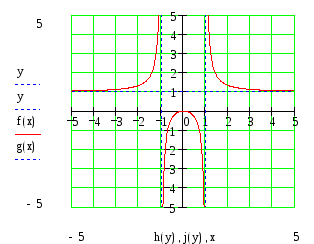

165. Дана функция
![]() .
Показать, что
.
Показать, что
![]()
Найдем
![]()
![]()
![]()
![]()
![]()
![]()
Что и требовалось показать.
175. Даны функции
![]() и две точки А(1,3) и В(0,96;2,95). Требуется: 1)
вычислить значение z1
функции в точке В; 2) вычислить приближенное
значение z1
функции в точке В, исходя из значений
z0
функции в точке А, заменив приращение
функции при переходе от точки А к точке
В дифференциалом, и оценить в процентах
относительную погрешность, возникающую
при замене приращения функции её
дифференциалом; 3) составить уравнение
касательной плоскости к поверхности
z=f(x,y)
в точке С(х0,у0,z0).
и две точки А(1,3) и В(0,96;2,95). Требуется: 1)
вычислить значение z1
функции в точке В; 2) вычислить приближенное
значение z1
функции в точке В, исходя из значений
z0
функции в точке А, заменив приращение
функции при переходе от точки А к точке
В дифференциалом, и оценить в процентах
относительную погрешность, возникающую
при замене приращения функции её
дифференциалом; 3) составить уравнение
касательной плоскости к поверхности
z=f(x,y)
в точке С(х0,у0,z0).
1)
![]()
2) Будем рассматривать
z(B)
как частное
значение функции
![]() при x
= 0.96 = x1,
у = 2.95 = у1.
За x0
принимаем число 1, за у0
–число 3.
при x
= 0.96 = x1,
у = 2.95 = у1.
За x0
принимаем число 1, за у0
–число 3.
Тогда z(x0,y0)
=
![]() ;
;
Переведём dx в радианы dx = x1 – x0 =0,96-1= –0,04,
dy = y1 –y0 = 2,95-3= -0,05
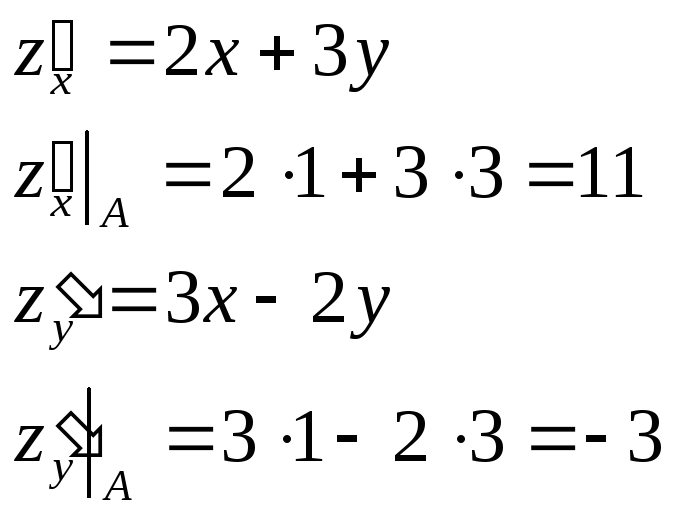
Тогда получим:
![]() z(x0,y0)
+
z(x0,y0)
+![]() (x0,y0)dx+
(x0,y0)dx+![]() (x0,y0)dy=1+11*(-0.04)-3*(-0.05)=0,71
(x0,y0)dy=1+11*(-0.04)-3*(-0.05)=0,71
Оценим погрешность:
![]() %
%
3) Составим уравнение
касательной плоскости к поверхности
z=f(x,y)
в точке С(1,2,11). Искомое уравнение имеет
вид:
![]() .
.

![]()
4. Неопределённый интеграл
185. Найти неопределенные интегралы (в случаях «а» и «б» проверить дифференцированием) :
а)

Проверим результат дифференцированием:

б)
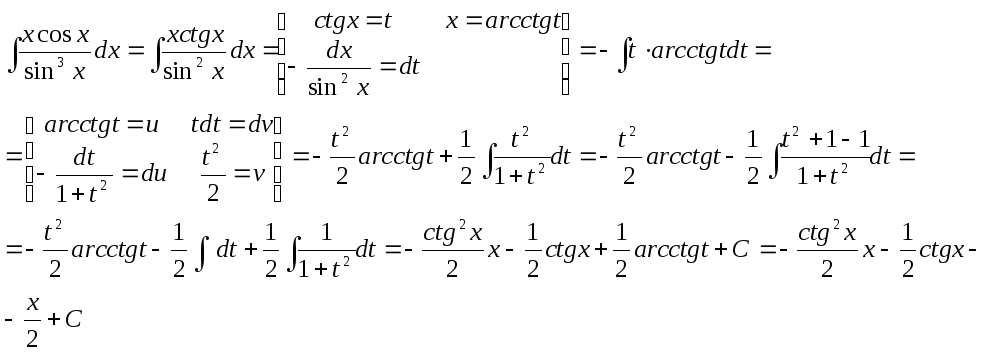
Проверим результат дифференцированием:

в)
![]()
Разобьём дробь на множители:
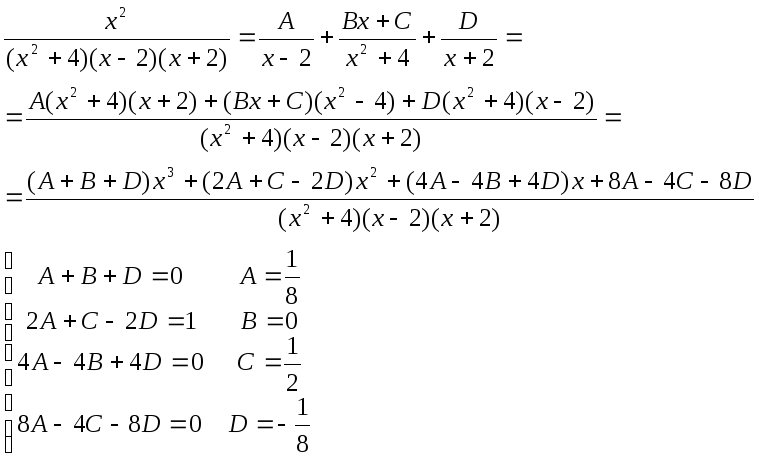

г)

д)
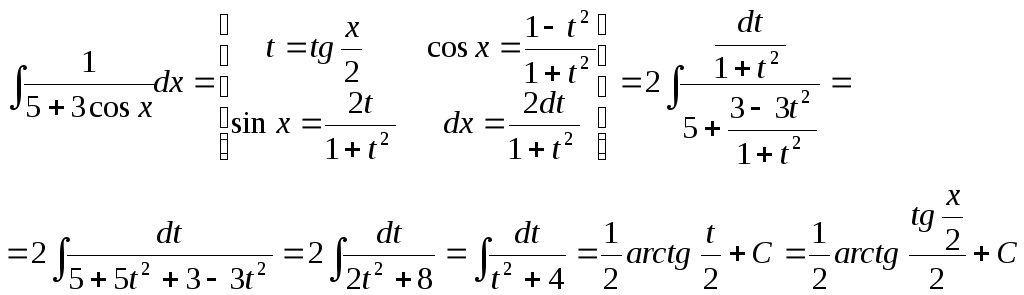
195. Вычислить определённый интеграл:
![]()
205. Вычислить несобственный интеграл или доказать его расходимость:

215. Вычислить
площадь фигуры, ограниченной трёхлепестковой
розой
![]() .
.
Сделаем чертёж


