
ФЗО, ИТиУвТС, Вариант 6, контрольная работа номер 2 по теме Введение в анализ
.docx2. Введение в анализ
76. Построить
график функции
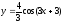 преобразованием графика функции y=sinx.
преобразованием графика функции y=sinx.
Записав данную
функцию в виде
 замечаем, что у неё А=
замечаем, что у неё А=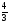 ,
,
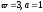 .
.
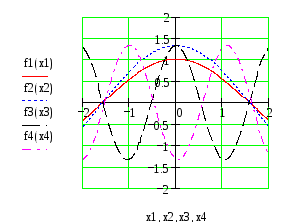
1. Строим одну волну косинусоиды и отмечаем на ней несколько точек.
2. Увеличивая в 4/3
раза ординаты выбранных точек графика
функции и оставляя неизменными абсциссы,
затем, отображая полученную линию
зеркально относительно оси ОХ, графика
y=cosx,
строим график функции
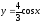 .
.
3. Увеличивая в 3
раза абсциссы точек графика функции
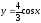 и
сохраняя неизменными ординаты, строим
график функции
и
сохраняя неизменными ординаты, строим
график функции
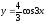 .
.
4. Перенося точки
графика функции
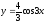 в направлении оси абсцисс на 1 единицы
масштаба этой оси влево, строим искомый
график функции
в направлении оси абсцисс на 1 единицы
масштаба этой оси влево, строим искомый
график функции
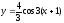 .
.
y=cosx y=4/3cosx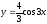
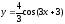
86. Линия задана
уравнением
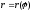 в
полярной системе координат. Требуется:
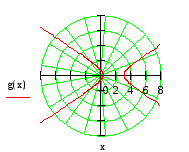
1) построить линию по точкам начиная от
φ=0 до φ=2π и придавая φ значения через
промежуток π/8; 2) найти уравнение данной
линии в декартовой прямоугольной системе
координат, у которой начало совпадает
с плюсом, а положительная полуось абсцисс
– с полярной осью и по уравнению в
декартовой прямоугольной системе
координат определить, какая это линия.
в
полярной системе координат. Требуется:
1) построить линию по точкам начиная от
φ=0 до φ=2π и придавая φ значения через
промежуток π/8; 2) найти уравнение данной
линии в декартовой прямоугольной системе
координат, у которой начало совпадает
с плюсом, а положительная полуось абсцисс
– с полярной осью и по уравнению в
декартовой прямоугольной системе
координат определить, какая это линия.
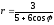
1)
|
φ |
r |
|
0 |
0,27 |
|
π/8 |
0,28 |
|
π/4 |
0,32 |
|
3π/8 |
0,41 |
|
π/2 |
0,60 |
|
5π/8 |
1,11 |
|
3π/4 |
3,96 |
|
7π/8 |
-5,52 |
|
π |
-3,00 |
|
9π/8 |
-5,52 |
|
5π/4 |
3,96 |
|
11π/8 |
1,11 |
|
3π/2 |
0,60 |
|
13π/8 |
0,41 |
|
7π/4 |
0,32 |
|
15π/8 |
0,28 |
|
2π |
0,27 |
2) Найдем уравнение данной линии в декартовой прямоугольной системе координат
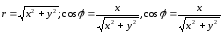
Подставим это значение в уравнение линии:
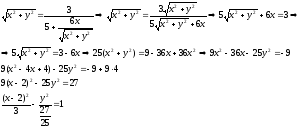
Это уравнение данной линии в декартовой системе координат.
Эта линия является гиперболой.
96. Найти пределы функций, не пользуясь правилом Лопиталя:
а)
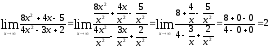
б)
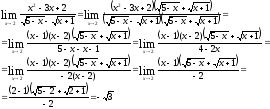
в)
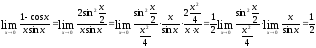
г)
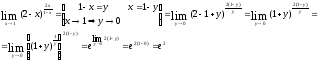
106.
Дана функция
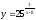 и два значения аргумента х1=10,
х2=8.
Требуется: установить, является ли
данная функция непрерывной или разрывной
для каждого из данных значений х; 2) в
случае разрыва функции найти ее пределы
при приближении к точке разрыва слева
и справа; 3) сделать схематический
чертеж..
и два значения аргумента х1=10,
х2=8.
Требуется: установить, является ли
данная функция непрерывной или разрывной
для каждого из данных значений х; 2) в
случае разрыва функции найти ее пределы
при приближении к точке разрыва слева
и справа; 3) сделать схематический
чертеж..
Данная функция определена и непрерывна на интервалах (-∞;8),(8;+∞).
Исследуем поведение функции в точках х1=10, х2=8. Найдём односторонние пределы.
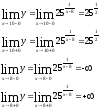
При х=10 функция имеет одинаковые односторонние пределы, значит, в этой точке функция непрерывна. При х=8 функция имеет бесконечные пределы, значит, в этих точках функция разрывна.
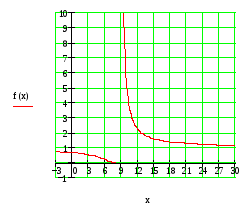
116. Задана функция y=f(x) различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать чертеж.
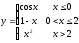
Данная функция определена и непрерывна на интервалах (-∞;0], (0,2],(2;+∞), где она задана непрерывными элементарными функциями. Исследуем поведение функции. В точках перехода от одного аналитического выражения к другому, т.е. в точках х=0 и х=2. Найдём односторонние пределы.
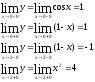
При х=0 функция имеет одинаковые односторонние пределы, значит, в этой точке функция непрерывна. Т.к. односторонние пределы при х=2 различны, то функция терпит в точке разрыв. А т.к. односторонние пределы конечны, то х=2 – точка разрыва первого рода. Функция имеет скачок в этой точке равный 4+1=5.
График этой функции:
