
Высшая математика, 1 курс, 1 семестр, КР №1, 2011
.docУчреждение образования
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет дистанционного образования
Специальность: маркетинг
Контрольная работа
ПО ВЫСШЕЙ МАТЕМАТИКЕ № 1 (часть 1)
вариант № 1
Задача 1. Даны векторы a,b,c,d. Требуется:
1)
вычислить скалярное произведение
векторов для векторов
![]() и
и
![]() ;
;
2)
найти модуль векторного произведения
векторов
![]() и
и
![]() ;
;
3)
проверить коллинеарность и ортогональность
векторов
![]() и
и
![]() ;
;
4) убедиться, что векторы a,b,c образуют базис;
5) найти координаты вектора d в этом базисе.
a=i-2j+3k, b=4i+7j+2k, c=6i+4j+2k, d=14i+18j+6k;
![]()
Решение:
-
Вычислим скалярное произведение векторов 3a и -2b:
![]()
![]()
![]()
-
Найдем модуль векторного произведения векторов -2b и с:
![]()
![]()
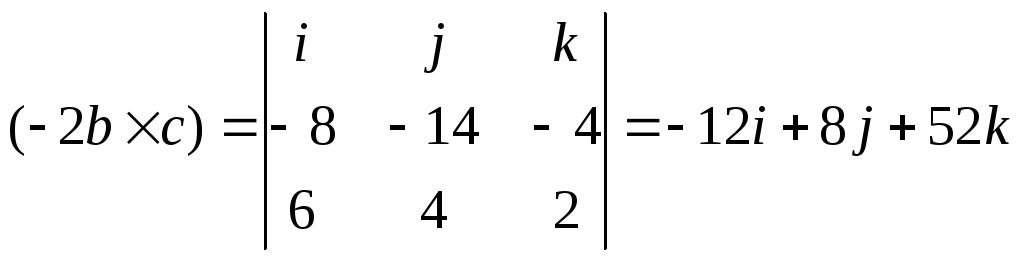
![]() ;
;
-
Проверим коллинеарность и ортогональность векторов 3a и c.
![]()
![]()
![]() ->
векторы неколлинеарны;
->
векторы неколлинеарны;
![]() ->
векторы неортогональны
->
векторы неортогональны
-
Проверим, что векторы a, b, c образуют базис
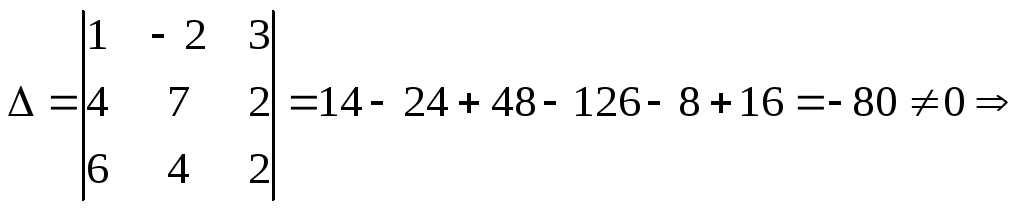 a,
b,
c
образуют базис
a,
b,
c
образуют базис
-
Найдем координаты вектора d в этом базисе:
![]()
![]()
Получим систему:
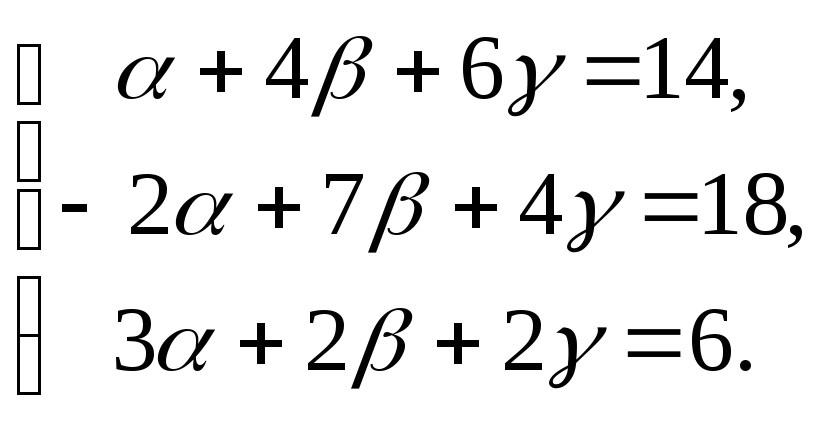
Воспользуемся правилом Крамера:
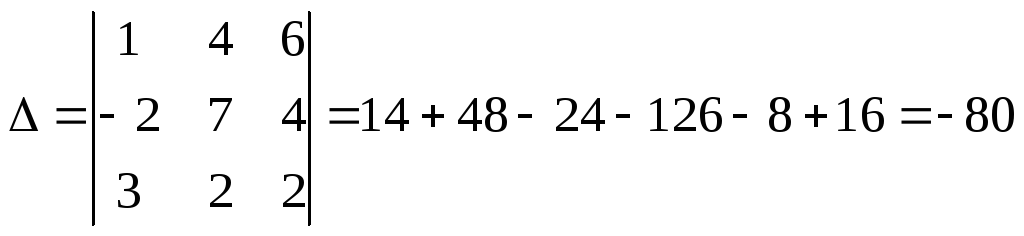
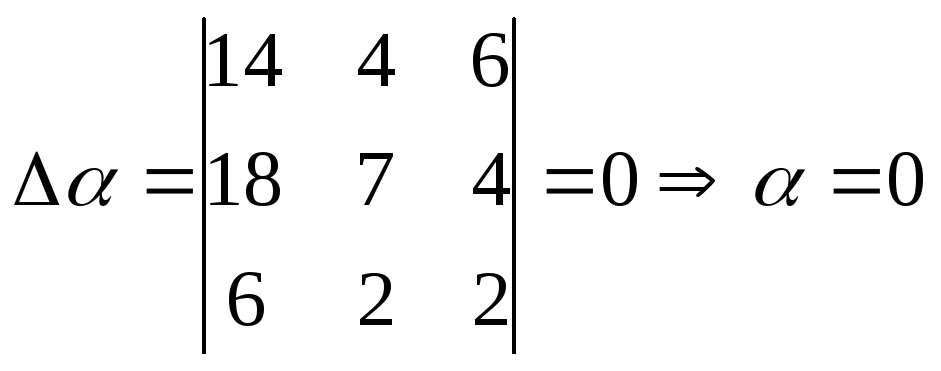

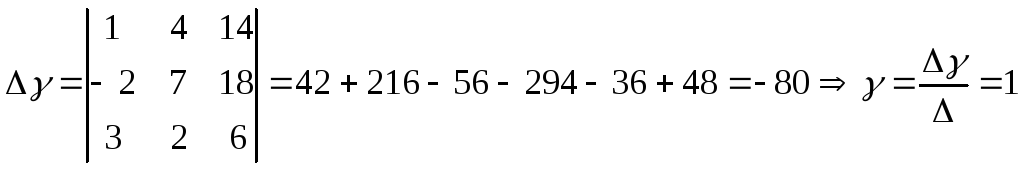
![]()
Ответ:
1) 24,
2)
4![]() ;
;
3) векторы неколлинеарны и неортогональны;
4) a, b, c образуют базис;
5) d=2b+c.
Задача 11. Даны вершины A(x1, y1), B(x2, y2), C(x3, y3) треугольника ABC. Требуется найти:
1) уравнение стороны AB;
2) уравнение высоты CH и длину этой высоты;
3) уравнение медианы AM;
4) точку N пересечения медианы AM и CH;
5) уравнение прямой, параллельной стороне AB и проходящей через вершину C;
6) внутренний угол при вершине A.
A(-2,4), B(3,1), C(10,7).
Решение:
1) Найти уравнение стороны AB.
Воспользуемся
формулой ![]() ,
где (x0,
y0)
и (x1,
y2)
–
координаты двух точек, принадлежащих
прямой:
,
где (x0,
y0)
и (x1,
y2)
–
координаты двух точек, принадлежащих
прямой:![]() .
.
![]() -
-![]() .
.
2) Найти уравнение высоты СН и длину этой высоты.
Т.к.
СН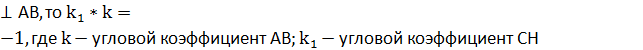 .
.
y
-
y0
= k
*(x
– x0),
где (x0,
y0)
– координаты точки прятой (в данном
случае С)
![]() ,
y-7=
,
y-7=
![]() (x
– 10), y
=
(x
– 10), y
= ![]() .
.
AB CH=H.
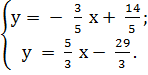
![]() =
= ![]() .
.
![]() =
=
![]() +
+ ![]() ,
Н(
,
Н(![]()
![]()
СН
= ![]() = 3
= 3![]() .
.
3) Найти уравнение медианы АМ.
М
(![]() ;
;
![]() ),
M(
),
M(![]() ,
4), т.к. yА
= yМ,
то уравнение АМ имеет вид y=4.
,
4), т.к. yА
= yМ,
то уравнение АМ имеет вид y=4.
4) Найти точку N пересечения AM и CH.
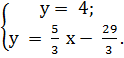
x=
![]() ,
y=
,
y=
![]() ,
N(
,
N(![]() ;
4).
;
4).
5) Найти уравнение прямой, параллельной стороне AB и проходящей через вершину С.
![]() ,
где (l,m)
– коорд. направляющего вектора.
,
где (l,m)
– коорд. направляющего вектора.
АВ(5, -3)- направляющий вектор.
![]() ,
30-3x=5y-35,
y
= -
,
30-3x=5y-35,
y
= - ![]() x
+ 13.
x
+ 13.
6) Найти внутренний угол при вершине А .
Внутренний угол при вершине А – это угол ВАС.
cosВАС
= ![]() =
= ![]() =
= ![]() ,
ВАС=45°.
,
ВАС=45°.
Ответ:
-
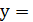 -
-
-
y =
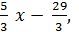 3
3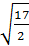 ;
; -
y=4;
-
(
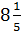 ;
4);
;
4); -
y = -
 x + 13;
x + 13; -
45°.
Задача 21. Составить канонические уравнения
1) эллипса,
2) гиперболы,
3) параболы
по
известным из условий 1 – 3 параметрам.
Через a
и
b
обозначены большая и малая полуоси
эллипса или гиперболы, через F
– фокус кривой,
![]() –
эксцентриситет, 2
c
–
фокусное расстояние,
–
эксцентриситет, 2
c
–
фокусное расстояние,
![]() – уравнения асимптот гиперболы, D
–
директриса кривой, A,
B–
точки, лежащие на кривой.
– уравнения асимптот гиперболы, D
–
директриса кривой, A,
B–
точки, лежащие на кривой.
![]()
Решение:
1)
Каноническое уравнение эллипса имеет
вид: ![]() +
+ ![]() = 1, (a>0,
b>0).
= 1, (a>0,
b>0).
F – фокус кривой и имеет координаты (c, 0) или (- с, 0).
с2=a2 – b2, отсюда находим a2= с2+ b2.
По условию с=10, a2=100 + 225= 325.
Каноническое
уравнение эллипса будет иметь вид: ![]() +
+ ![]() = 1.
= 1.
2)
Каноническое уравнение гиперболы имеет
вид: ![]() -
- ![]() = 1.
= 1.
Эксценриситет
ε
=![]() ,
т.к. по условию ε=14/13,
то с = 14.
,
т.к. по условию ε=14/13,
то с = 14.
Из с2=a2 + b2 находим b2 = 27.
Получаем
следующее уравнение: ![]() -
- ![]() = 1.
= 1.
3)
Каноническое уравнение параболы,
директриса которой задается уравнение
x=const,
имеет вид: ![]()
x=
![]() = -4 (по условию), p
= 8.
= -4 (по условию), p
= 8.
![]() .
.
Ответ:
-
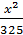 +
+ 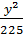 = 1;
= 1; -
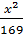 -
- 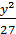 = 1;
= 1; -
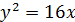 .
.
Задача 31. Даны четыре точки A1(x1,y1,z1), A2(x2,y2,z2), A3(x3,y3,z3), A4(x4,y4,z4). Требуется найти:
1) уравнение плоскости A1A2A3;
2) уравнение прямой, проходящей через точку A4, перпендикулярно плоскости A1A2A3;
3) расстояние от точки A4 до плоскости A1A2A3;
4) синус угла между прямой A1A4 и плоскостью A1A2A3;
5) косинус угла между координатной плоскостью Oxy и плоскостью A1A2A3.
A1(3,-1,2), A2(-1,0,1), A3(1,7,3), A4(8,5,8).
Решение:
1) Найти уравнение плоскости А1А2А3.
Уравнение плоскости, проходящей через три заданные точки А1(x1, y1,z1), А2(x2, y2,z2), А3(x3, y3,z3), может быть записано в виде:
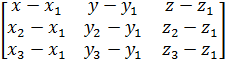 =
0
=
0
Подставим в это равенство координаты точке А1, А2, А3.
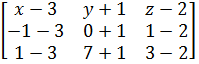 =
=
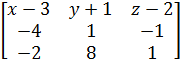 = 9 x
+ 6 y
- 30 z
+ 39=0.
= 9 x
+ 6 y
- 30 z
+ 39=0.
2) Найти уравнение прямой L, проходящей через точку A4 перпендикулярно плоскости А1А2А3.
В параметрическом виде уравнение прямой имеет вид:
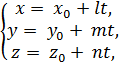 где (x0,
y0,
z0)
– произвольная точка прямой, a(l,
m,
n)
– направляющий вектор прямой, t
R.
где (x0,
y0,
z0)
– произвольная точка прямой, a(l,
m,
n)
– направляющий вектор прямой, t
R.
Плоскость А1А2А3: 9 x + 6 y - 30 z + 39=0. Тогда вектор нормали плоскости А1А2А3: n(9, 6, -30). Вектор n перпендикулярен плоскости А1А2А3, а значит, будет являться направляющим вектором прямой L. Тогда прямая L:
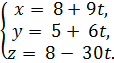
3) Найти расстояние от точки А4 до плоскости А1А2А3.
Растояние от точки А(x0, y0, z0) до плоскости Ax + By + Cz +D=0 определяется формулой:
d
= ![]() .
.
Тогда расстояние от А4(8, 5, 8) до А1А2А3 будет равно:
d
= ![]() =
= ![]() =
= ![]() .
.
4) Найти синус угла между прямой А1А4 и плоскостью А1А2А3.
Если a(l, m, n) – направляющий вектор прямой, а n(A, B, C) – вектор нормали плоскости, то синус угла α между прямой и плоскостью вычисляет по формуле:
sin
α
= ![]() =
=
![]() .
.
Вектор А1А4 будет являться направляющим вектором прямой А1А4. Координаты вектора А1А4=(5, 6, 6).
Вектор нормали плоскости А1А2А3 n(9, 6, -30).
sin
α
= ![]() =
=
![]() .
.
5) Найти косинус угла между координатной плоскостью Оxy и плоскостью А1А2А3.
Вектор нормали к плоскости Оxy n1(0, 0, 1), а к плоскости А1А2А3 n(9, 6, -30).
Длины
этих векторов |n1|
= 1, |n|=3![]() .
Тогда косинус угла
между плоскость Oxy
и А1А2А3
равен:
.
Тогда косинус угла
между плоскость Oxy
и А1А2А3
равен:
cos
= ![]() =
= ![]() = -
= - ![]() = -
= - ![]() .
.
Ответ:
-
9 x + 6 y - 30 z + 39=0;
-
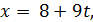
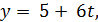
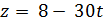 ;
; -
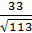 ;
; -
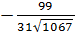 ;
; -
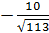 .
.
