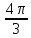Контрольная работа №6
.docx265. Найти неопределенные интегралы. В случаях а и б проверить дифференцированием



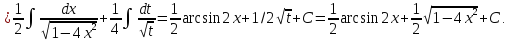
Проверка дифференцированием





Проверка дифференцированием



Разлагаем функцию на простые дроби

Приведем к общему знаменатели и приравняем числители
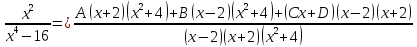

Сравниваем коэффициенты при одинаковых степенях слева и справа

Получаем:

подставляем в схему разложения
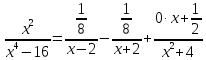
При
решении интеграла применяем подстановку
 ,
тогда
,
тогда
 и подстановку
и подстановку
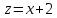 ,
тогда
,
тогда
 .
.



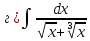











275. Вычислить определенный интеграл. Окончательный результат представить в виде приближенного числа.
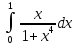
Применяем
подстановку
 тогда
тогда
 .
.
Находим
новые пределы интегрирования
 при
при
 ,
,
 при
при


285. Вычислить несобственный интеграл или доказать его расходимость.

Данный интеграл является несобственным интегралом 1 рода , который определяется как предел соответствующего определенного интеграла.



Данный интеграл является несобственным интегралом 2 рода с несуществующей подынтегральной функцией в верхнем пределе


295.
Вычислить площадь фигуры, ограниченной
трехлепестковой розой

Площадь фигуры, ограниченная кривой, определяется по формуле:

Строим
кривую
 по точкам
по точкам
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
5 |
3,5 |
0 |
-5 |
0 |
3,5 |
5 |
0 |
-5 |
-3,5 |
0 |
5 |
0 |
-3,5 |
-5 |
0 |
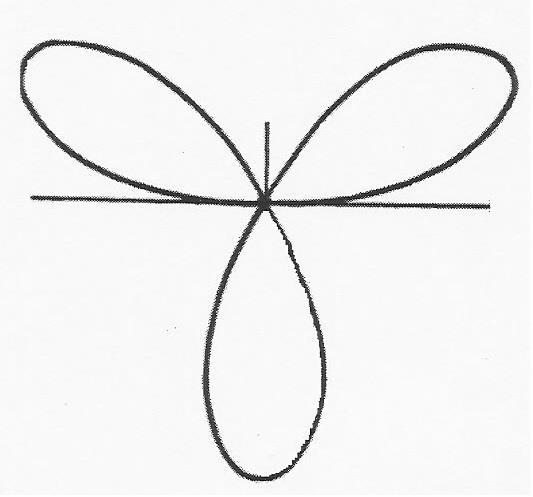
Полная
площадь, ограниченная кривой, равна
шестикратной площади части, соответствующей
изменению
 от 0 до
от 0 до