контрольная работа вариант-9

Вариант 9

№319 Исследовать сходимость числового ряда

Решение

Т.к.

По признаку сравнения исходный ряд можно сравнить с рядом

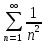
Который сходится по интегральному признаку

Из сходимости следует сходимость

Ответ. Ряд сходится.

№329. Найти интервал сходимости степенного ряда

Решение

Найдем радиус сходимости

Интервал сходимости

№339 Вычислить определенный интеграл с точностью до 0,001. Для этого подынтегральную функцию следует разложить в ряд, который затем почленно проинтегрировать.

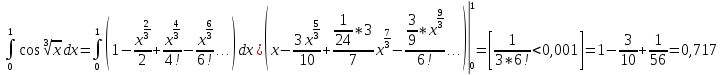
Ответ. 0.717

№349 Найти три первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения, удовлетворяющего начальному условию

Решение

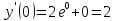
Найдем :

Найдем :

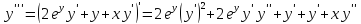
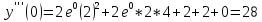
Тогда решение примет вид:

Ответ

№ 359. На интервале задана периодическая с периодом функция 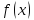. Требуется

1. Разложить функцию в ряд Фурье

2. Построить график суммы ряда Фурье

Решение

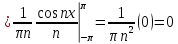
Тогда ряд Фурье примет вид

Нарисуем график

№369. Представить заданную функцию , где , в виде 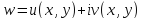; проверить, является ли она аналитической. Если да, то найти значение ее производной в заданной точке

Решение

Проверим, является ли функция аналитической

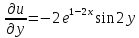
Найдем производную в точке

№379 Разложить функцию в ряд Лорана в окрестности точки :

Решение

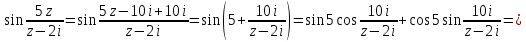
№389 Определить область (круг) сходимости данного ряда и исследовать сходимость его (расходится, сходится условно, сходится абсолютно) в точках z1, z2, z3

Решение

Найдем радиус сходимости

Тогда ряд сходится в круге

1. , значит в этой точке ряд сходится абсолютно.

2. 

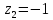
Исследуем ряд из модулей

По интегральному признаку

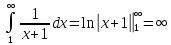
расходится

Проверим признак Лейбница

1

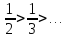
2

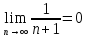
Условие Лейбница выполняется, значит ряд сходится условно.

3. лежит за кругом сходимости, а значит в ряд расходится.

№399. При помощи вычетов вычислить данный интеграл по контуру .

Решение.

- полюсь первого порядка

- полюс второго порядка

Найдем вычеты

Тогда

№409 Найти изображение заданного оригинала .

Решение

Ответ.

№419. Найти изображение заданного оригинала .

Решение

Тогда

Ответ

№429. Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям:

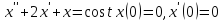
Решение

Подставим в уравнение

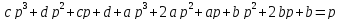
Ответ.