
Контрольная 7, 5 вариант
.doc345.) Найти общее решение дифференциального уравнения первого порядка:
![]()
Решение:
Найдем

![]()
Составим разность
![]()

Вычислим интегрирующий множитель
![]()
После умножения на r(x) уравнение становится точным:
![]()
Его общий интеграл имеет вид U(x,y)=C, где
U(x,y)=F(x,y)+G(x,y),
![]()
Посчитаем отдельно
![]() ,
пусть
,
пусть
![]() ,
,
![]() ,
,
![]()

![]()
![]()
![]()
![]() - общий интеграл дифференциального
уравнения
- общий интеграл дифференциального
уравнения
355.) Найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям.
![]() ,
,
![]()
![]()
Решение:
а) Соответствующее характеристическое уравнение имеет вид
![]() ,
корни уравнения
,
корни уравнения
![]() .
.
б) Правая часть уравнения не является
специальной правой частью, но может
быть представлена как сумма двух
специальных частей
![]() =
2sin2x и
=
2sin2x и
![]() =
2x. Найдем частные решения
для каждой из них, а затем, используя
метод суперпозиции, напишем искомое
частное решение для всей правой части
=
2x. Найдем частные решения
для каждой из них, а затем, используя
метод суперпозиции, напишем искомое
частное решение для всей правой части
![]()
![]() - вычислим контрольное число правой
части
- вычислим контрольное число правой
части
![]() -
не корень характеристического уравнения,
следовательно, кратность r=0,
-
не корень характеристического уравнения,
следовательно, кратность r=0,
![]()
![]() - вычислим контрольное число правой
части
- вычислим контрольное число правой
части
![]() -
не корень характеристического уравнения,
следовательно, кратность r=0,
k=1
-
не корень характеристического уравнения,
следовательно, кратность r=0,
k=1
![]()
Частное решение для суперпозиции
![]() примет вид:
примет вид:
![]()
Для нахождения
![]() вычислим
вычислим
![]() и подствим их в исходное уравнение
и подствим их в исходное уравнение
![]()
![]()
Подставим найденные значения производных
в уравнение с правой частью
![]()
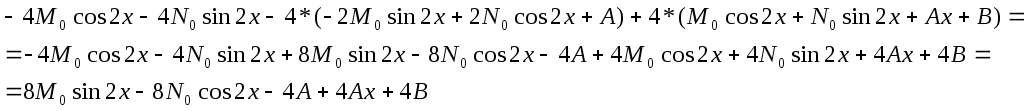
![]()
![]()
Решим систему:


Итак,
![]()
Запишем фундаментальную систему решений однородного уравнения.
Корни у нас равны и действительны, значит
![]() и
и
![]()
Запишем общее решение неоднородного уравнения:
![]()
Решим задачу Коши:
![]()

Решим систему


Найдено решение задачи Коши

365.) Найти общее решение системы уравнений (рекомендуем решать с помощью характеристического уравнения)

Решение:
Применим метод Эйлера. Запишем систему в матричной форме:
![]()
Будем искать частное решение в виде
![]() ,
,
![]() ,
где
,
где
![]() – константы. Составляем характеристическое
уравнение матрицы системы (E-единичная
матрица n-го порядка):
– константы. Составляем характеристическое
уравнение матрицы системы (E-единичная
матрица n-го порядка):
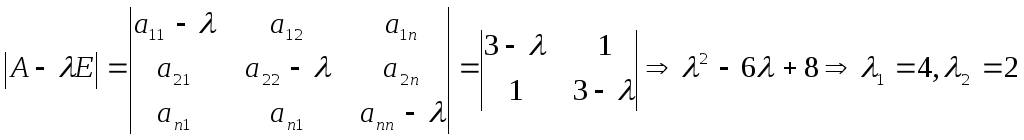
Находим
![]() и
и
![]() из системы уравнений
из системы уравнений

А) При
![]() получаем
получаем

Положив
![]() ,
получим
,
получим
![]() .
Таким образом, характеристическому
числу
.
Таким образом, характеристическому
числу
![]() соответствует частное решение
соответствует частное решение
![]()
Б) При
![]() получаем
получаем
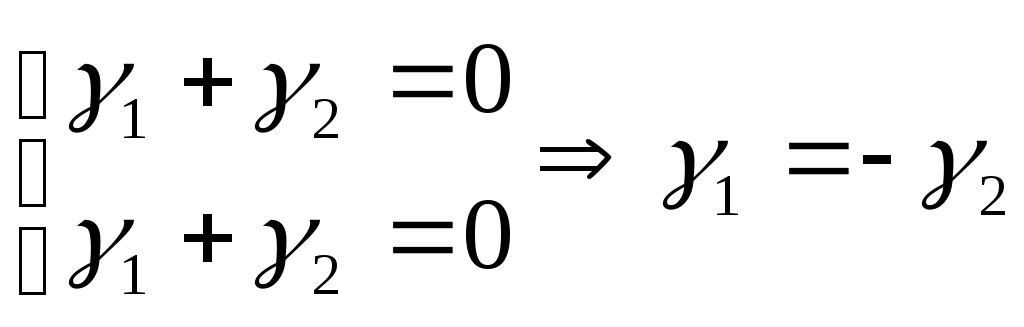
Положив
![]() ,
получим
,
получим
![]() .
Таким образом, характеристическому
числу
.
Таким образом, характеристическому
числу
![]() соответствует частное решение
соответствует частное решение
![]()
Общее решение системы находим как линейную комбинацию полученных частных решений, т.е.
![]()
375. По закону Ньютона скорость охлаждения тела в воздухе пропорциональна разности между температурой тела и температурой воздуха. Если температура воздуха равна 200С и тело в течение часа охлаждается от 100 до 300С, то через сколько минут (с момента начала охлаждения) его температура понизится до 600С?
Решение:
Пусть T-температура тела,
![]() -температура
окружающей среды,
-температура
окружающей среды,
![]() -количество
теплоты, с – удельная теплоемкость.
Тогда количество теплоты, передаваемое
окружающей среде при снижении температуры
тела выражается формулой
-количество
теплоты, с – удельная теплоемкость.
Тогда количество теплоты, передаваемое
окружающей среде при снижении температуры
тела выражается формулой
![]() или,
в деференциальной форме,
или,
в деференциальной форме,
![]() .
С другой стороны скорость отдачитепла
можно выразить в виде
.
С другой стороны скорость отдачитепла
можно выразить в виде
![]() ,
где k – некоторый коэффициент
пропорцианальности. Из этих уравнений
получаем:
,
где k – некоторый коэффициент
пропорцианальности. Из этих уравнений
получаем:
![]()
![]()
![]()
Итак из условия составим систему (в
момент t=0 и момент t=60),
для нахождения константы С и коэффициента
![]() :
:

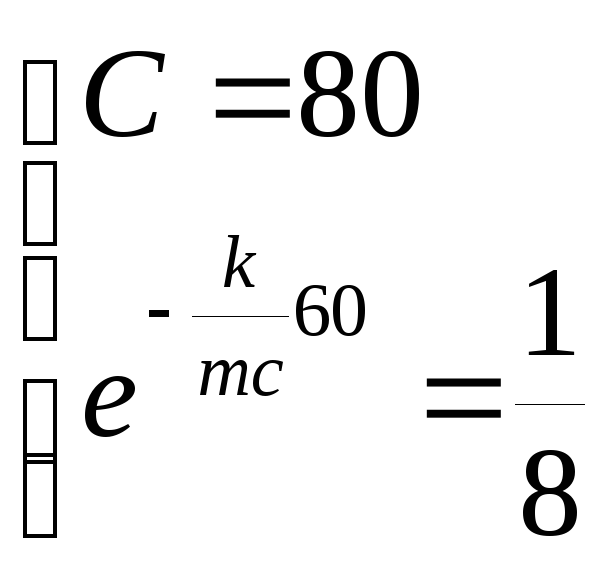


Температура понизится до 600С через

