
Решение:
Данная система имеет размер 2×3. Она однородна, т.к. свободный член в каждом уравнении равен нулю. Число уравнений меньше числа неизвестных. Следовательно, множество решений системы бесконечно.
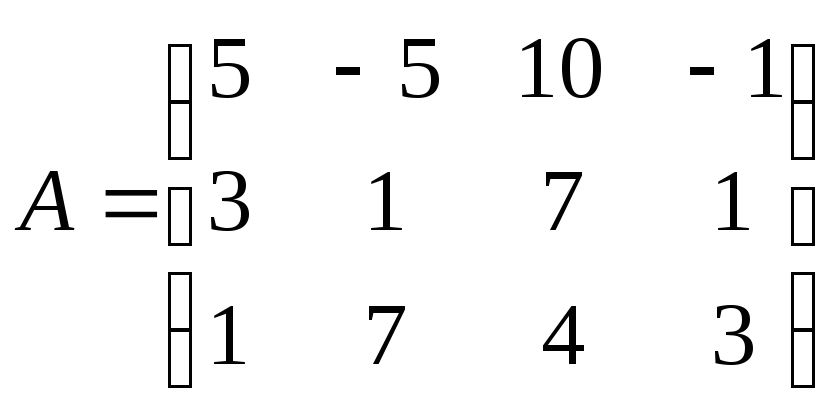 Проведем
преобразования:
Проведем
преобразования:
Для этого проведём преобразования матрицы А:
-
Отнимем от элементов первой строки элементы второй строки, умноженные на 2;
-
К первой строке добавим третью;
-
Третью строку умножим на 3 и вычтем из неё вторую строку;
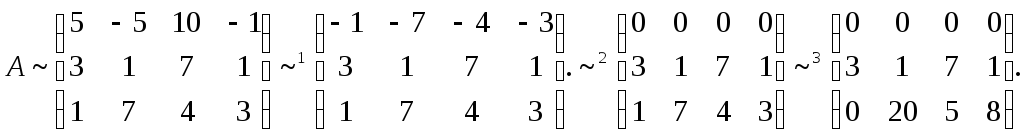
Ранг матрицы системы равен двум, так как только среди ее миноров
второго порядка
есть отличный от нуля, например минор
![]()
Следовательно, данная система эквивалентна системе
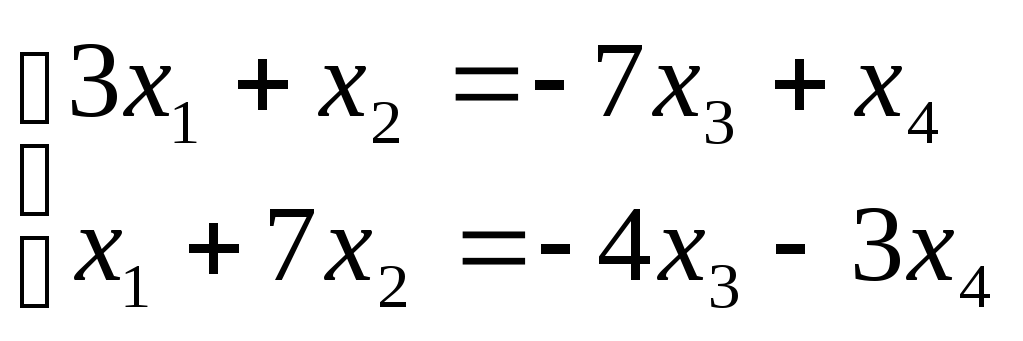 ,
,
Отсюда


Следовательно, множество решений системы имеет вид
![]() .
.
Задача 74.
Даны два линейных преобразования.
Средствами матричного исчисления найти
преобразование, выражающее
![]() через
через
![]()
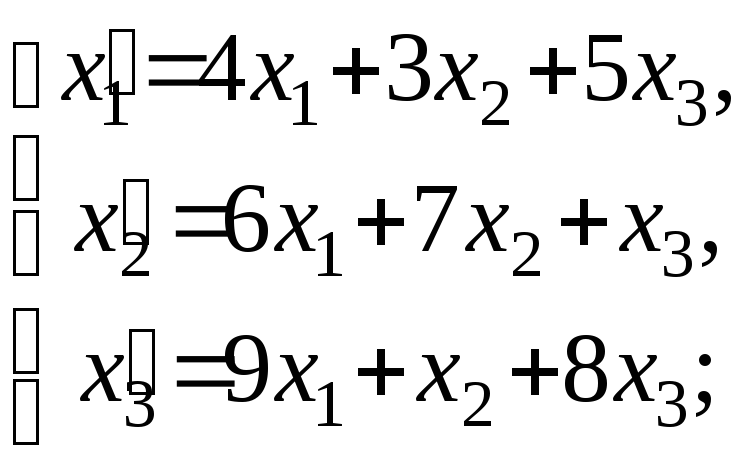
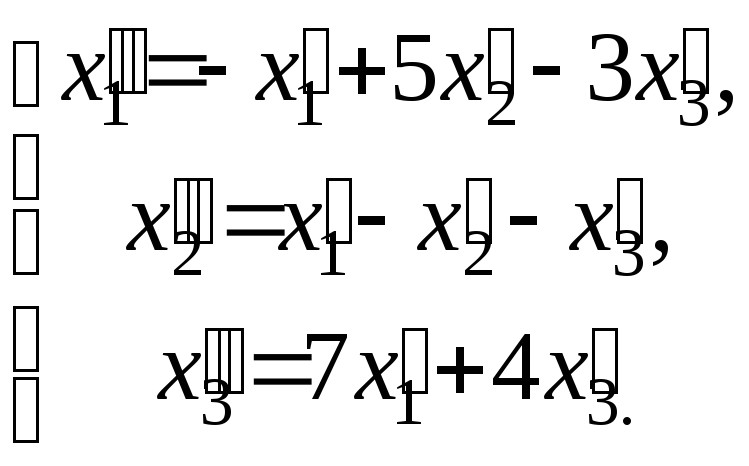
Решение:
Составим две матрицы:
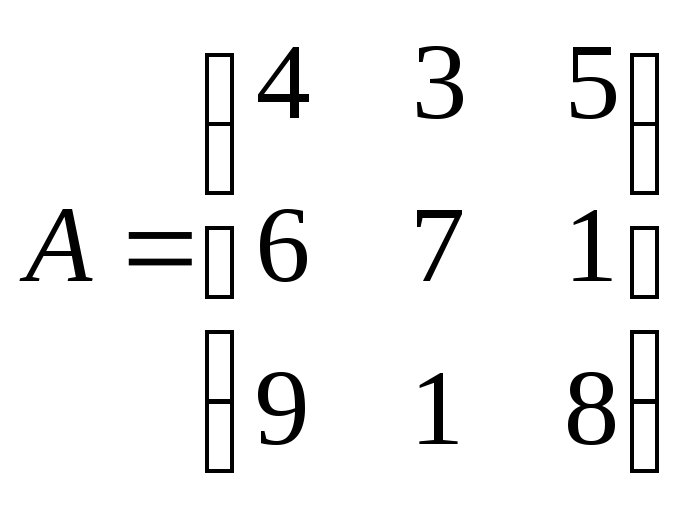 и
и
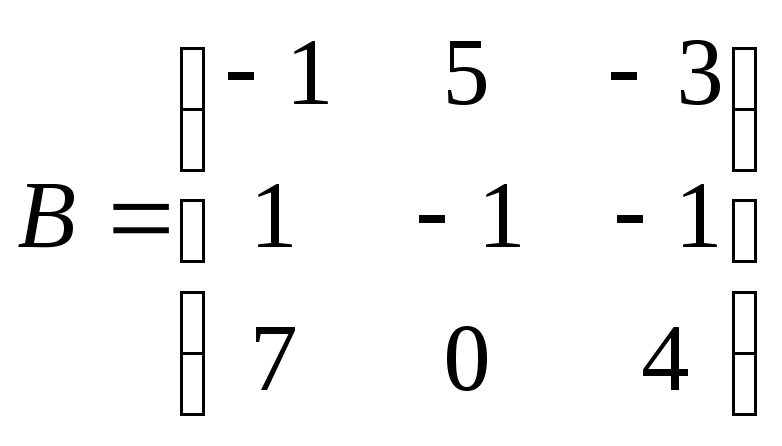
найдем их произведение:
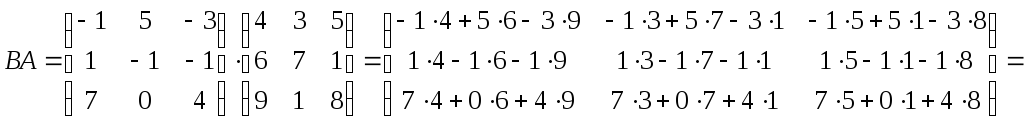
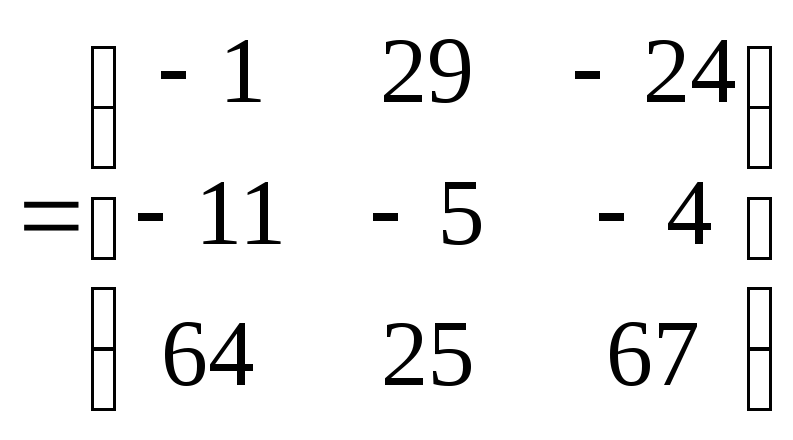
Поэтому искомое линейное преобразование имеет вид:
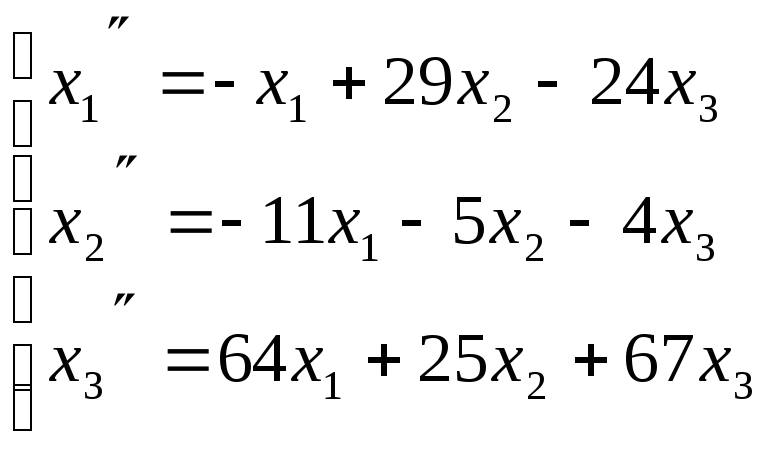
Задача 84. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

Решение:
-
Характеристическое уравнение данного преобразования имеет вид:
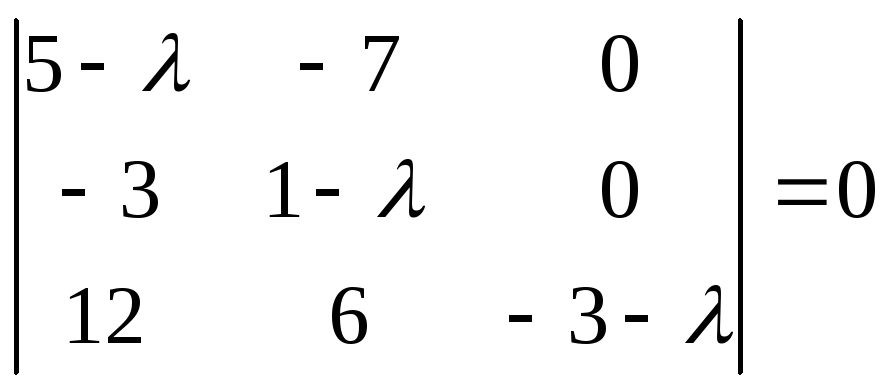
Корни этого
уравнения следующие:
![]() ;
;
![]() ;
;
![]()
-
Все корни являются собственными числами.
-
Чтобы найти собственный вектор с собственным числом
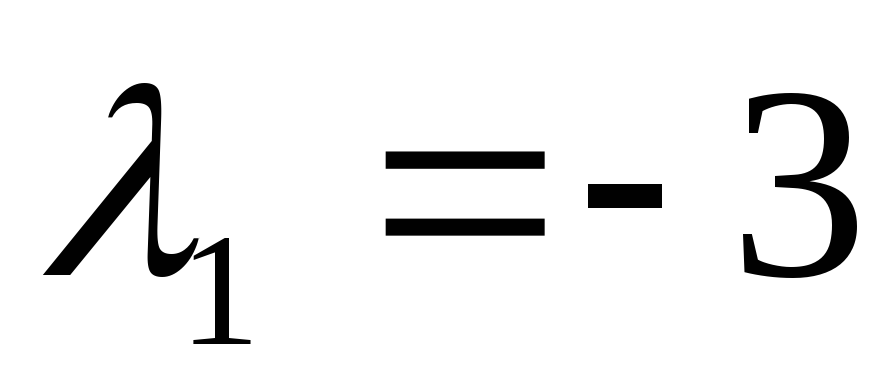 ,
полагаем в системе
,
полагаем в системе
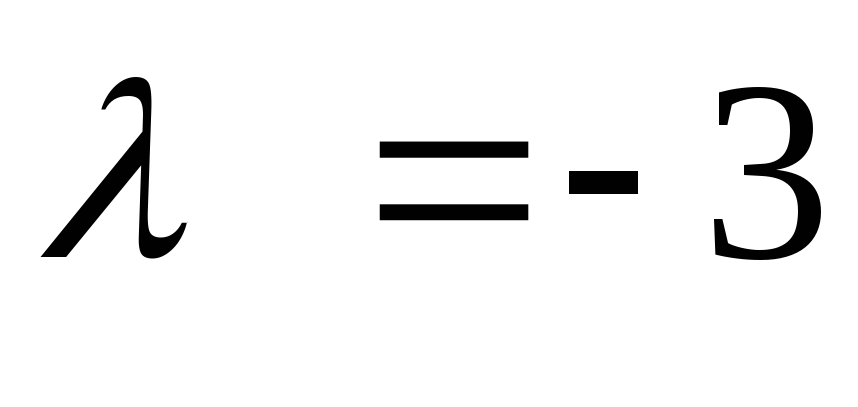 .
Получим
.
Получим
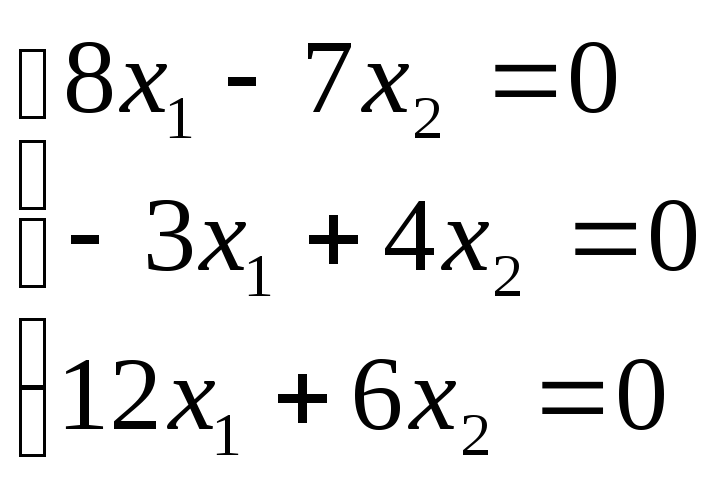
Решение этой системы можно записать в виде
![]() ;
;
![]() ;
;
![]()
Вектор
![]() ,
где
,
где
![]() и
и
![]() — любые числа, удовлетворяющие условию
— любые числа, удовлетворяющие условию
![]() ,
является собственным вектором данного
преобразования с собственным числом
,
является собственным вектором данного
преобразования с собственным числом
![]() .
.
-
Аналогично находим собственный вектор с собственным числом
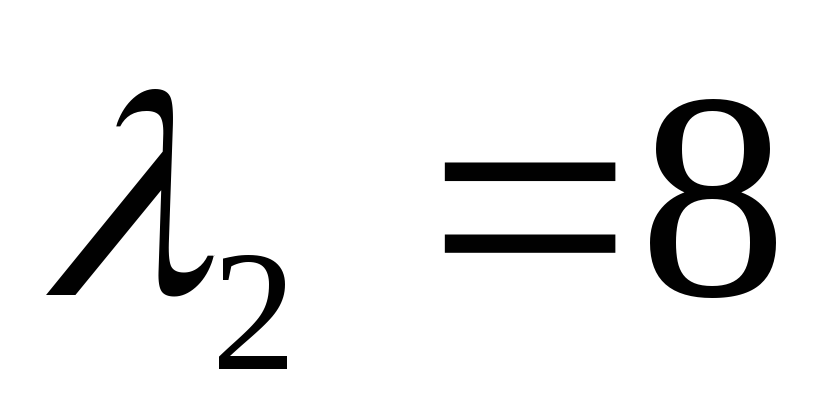 :
:
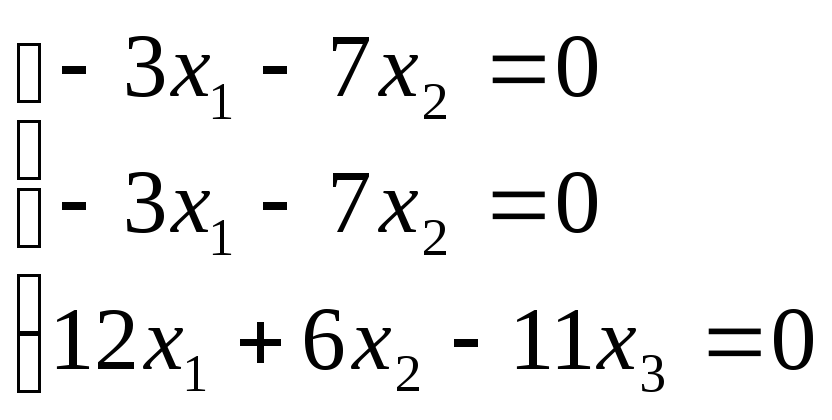
![]() ;
;
![]() ;
;
![]()
Вектор
![]() ,
где
,
где
![]() — любое число, удовлетворяющее условию
— любое число, удовлетворяющее условию
![]() ,
является собственным вектором данного
преобразования с собственным числом
,
является собственным вектором данного
преобразования с собственным числом
![]() .
.
-
Аналогично находим собственный вектор с собственным числом
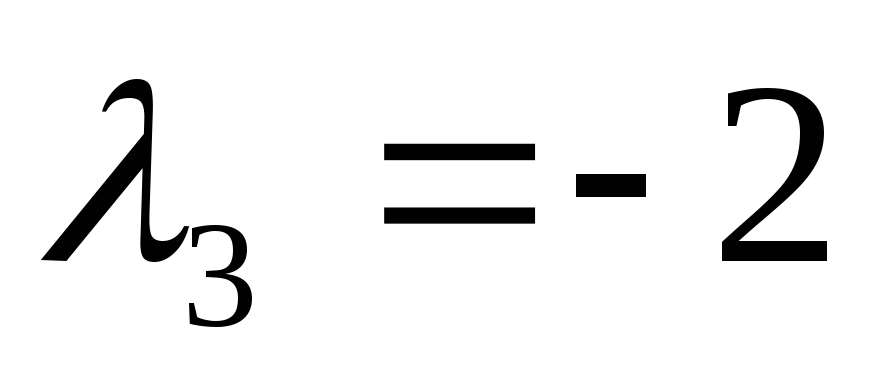 :
:
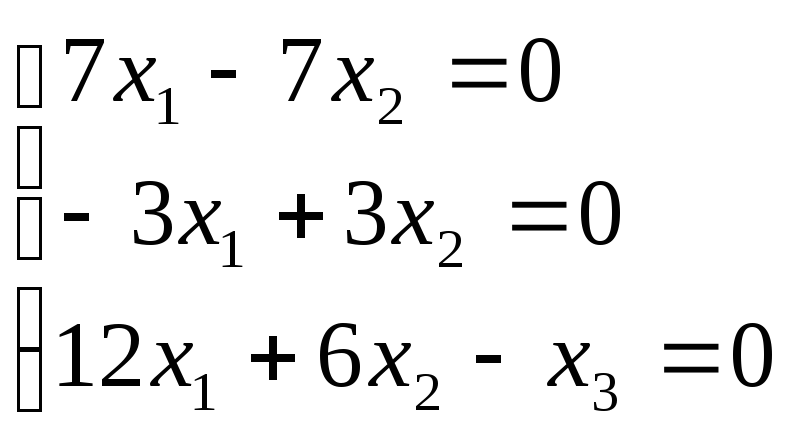
![]() ;
;
![]() ;
;
![]()
Вектор
![]() ,
где
,
где
![]() — любое число, удовлетворяющее условию
— любое число, удовлетворяющее условию
![]() ,
является собственным вектором данного
преобразования с собственным числом
,
является собственным вектором данного
преобразования с собственным числом
![]() .
.
Задача 94. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм.
![]()
Решение:
Введем обозначение![]() .
Тогда матрица данной квадратичной формы
.
Тогда матрица данной квадратичной формы
![]() .
.
Найдем собственные значения этой матрицы. Ее характеристическое уравнение имеет вид
![]() ,
,
откуда
![]() ;
;
![]() .
Тогда квадратичная форма имеет следующий
канонический вид:
.
Тогда квадратичная форма имеет следующий
канонический вид:
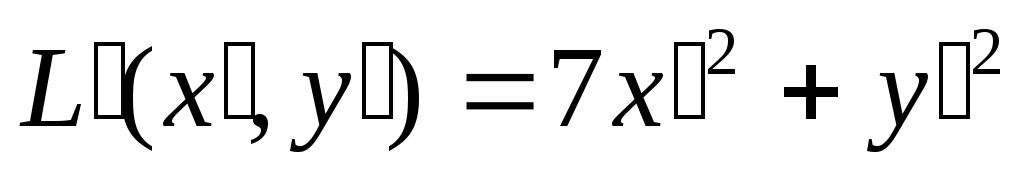 .
Переходя к исходному уравнению, получаем
.
Переходя к исходному уравнению, получаем
![]() .
Т.е. имеем эллипс
.
Т.е. имеем эллипс
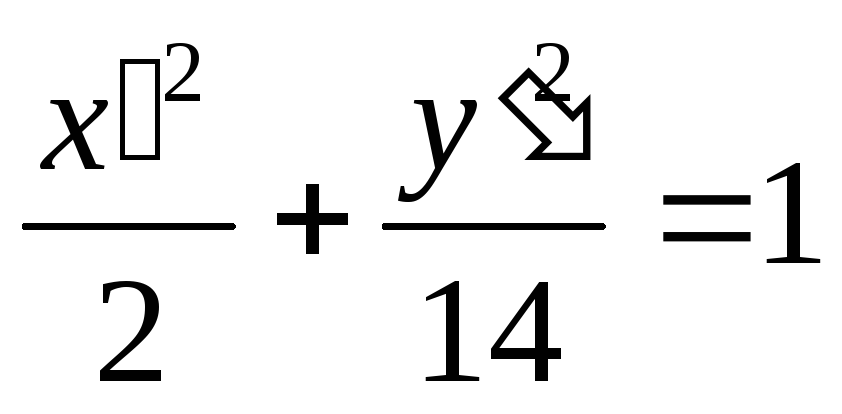
Задача 104.
Построить график функции
![]() преобразованием графика функции
преобразованием графика функции
![]() .
.
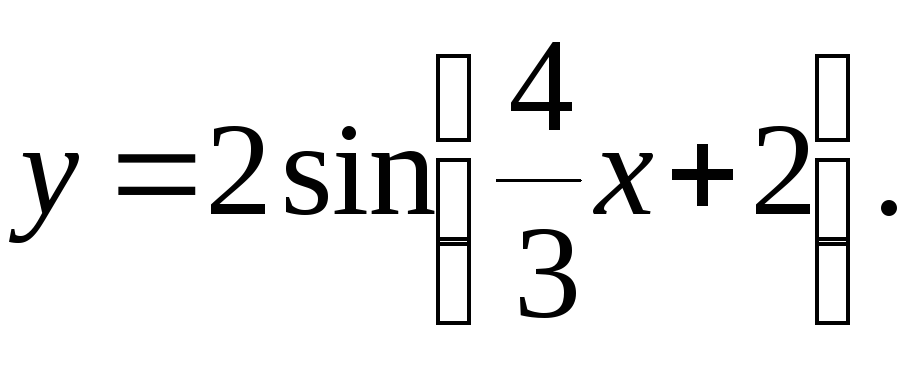
Решение:
-
Построим график функции
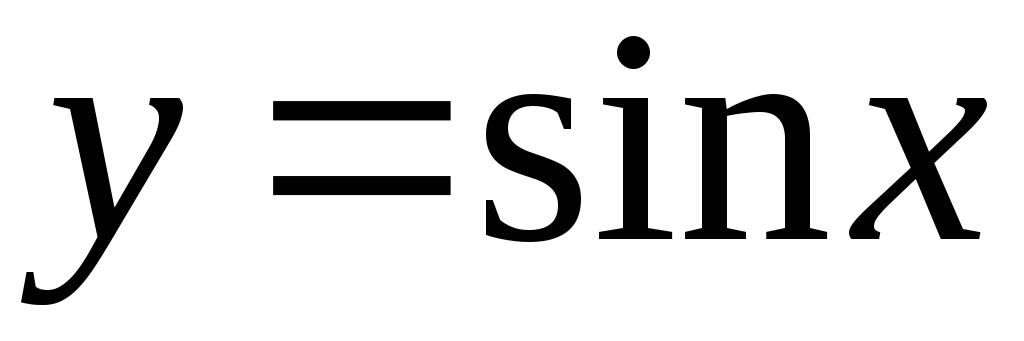 :
:

-
График общей синусоиды
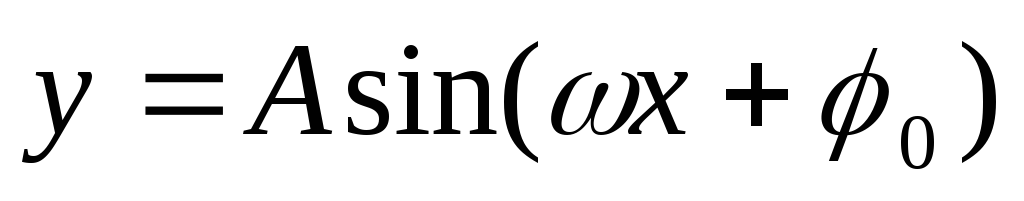 с амплитудой
с амплитудой
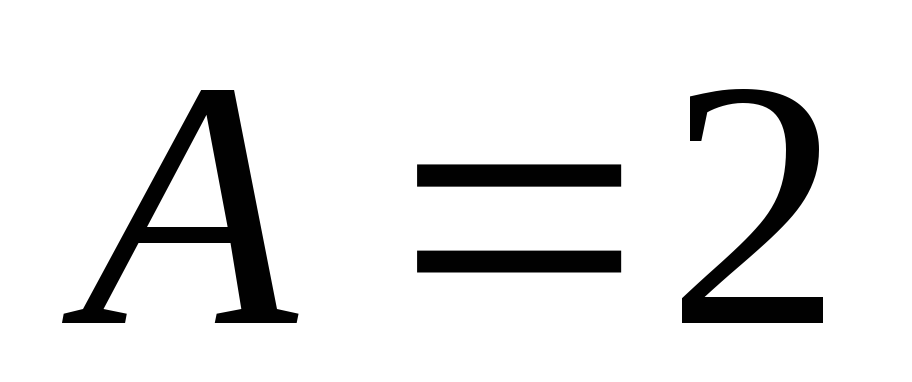 ,
круговой частотой
,
круговой частотой
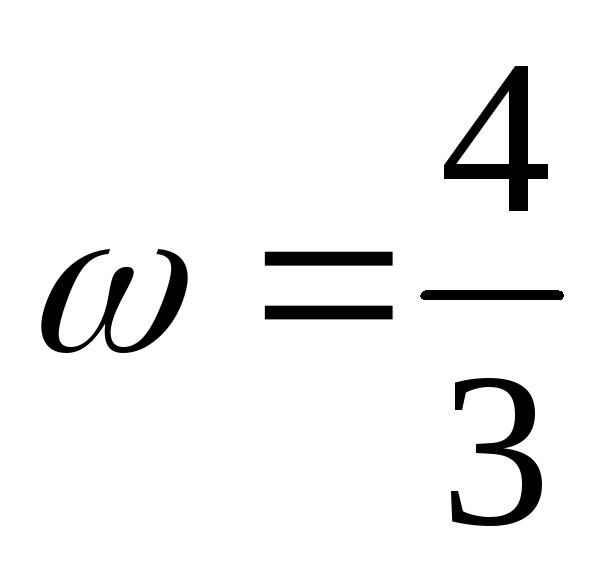 и
фазой
и
фазой
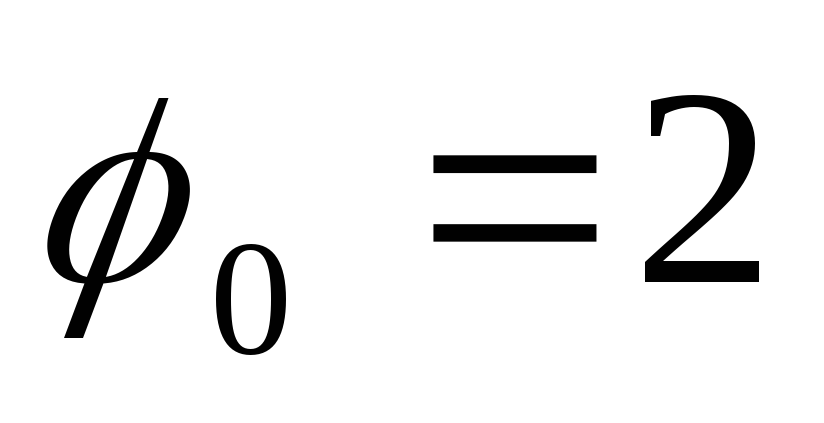 получим
синусоиды последствием преобразований:
получим
синусоиды последствием преобразований:
растяжением в
![]() раз
в направлении оси
раз
в направлении оси
![]() ,
,
растяжением в
![]() =
=![]() раз в направлении оси
раз в направлении оси
![]()
и последующим
параллельным переносом по оси
![]() на
на
![]() .
.

Задача 114.
Дана функция
![]() на отрезке
на отрезке
![]() .
Требуется:
.
Требуется:
1) построить график функции в полярной системе координат по точкам, давая значения через промежуток /8, начиная от =0;
2) найти уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить, какая это будет линия.
![]()
