Контрольная работа №4

Дифференциальное исчисление функций одной переменной

1)Вычислить: 1-3) производную ; 4) производные и ; 5) в данной точке x₀ (x₀); 6) производную n-го порядка для данной функции y(x).

1) 2)

3) 4)

5) , x₀=1; 6)

Решение.

1) ;

2) воспользуемся правилами вычисления производной произведения и производной сложной функции:

.

3) Сначала прологарифмируем, а затем возьмем производную от обеих частей.

;

Тогда

.

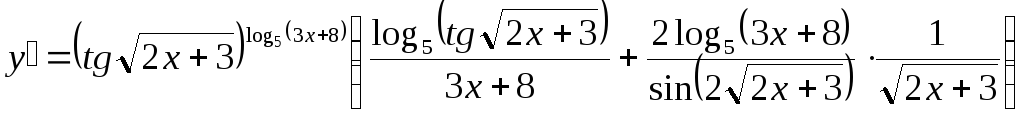4) Возьмем производную от обеих частей равенства

, т.е. .

Снова возьмем производную . Подставляя в последнее равенство выражение для первой производной, получим

.

5) Последовательно найдем третью производную

;

;

.

Вычислим значение третьей производной в точке x₀=1.

.

6)

.

2)Применяя формулу Тейлора с остаточным членом в форме Лагранжа, вычислить значение функции с точностью до 0,001.

.

Решение.

Выпишем формулу Тейлора с остаточным членом в форме Лагранжа:

и положим в ней, ,

Т.к. , то используя выражение для остаточного члена в форме Лагранжа, можно найти значение n, требуемое для получения заданной точности.

;

;

.

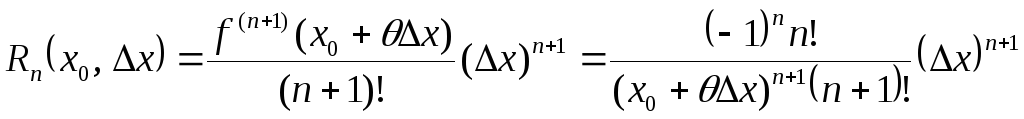Из последнего неравенства следует, что для определения требуемой точности достаточно взять n = 2. Тогда

;

.

3)Найти наибольшее и наименьшее значения функции на отрезке .

Решение.

Найдем производную

.

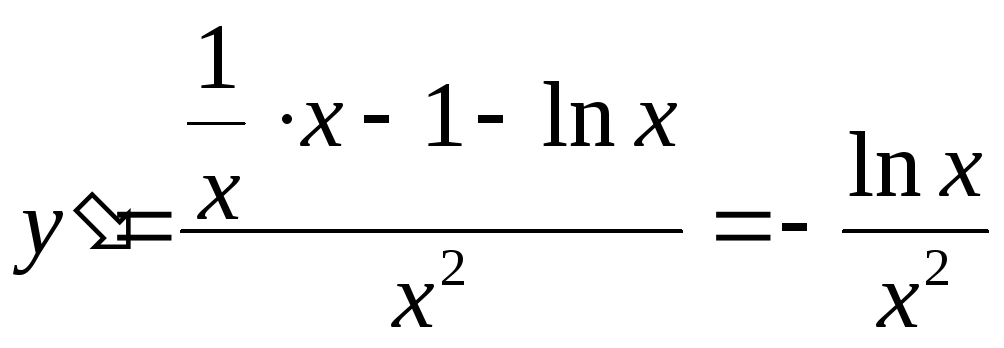Ясно, что .

Вычислим значения функции при х = 1 и на концах отрезка

;

;

.

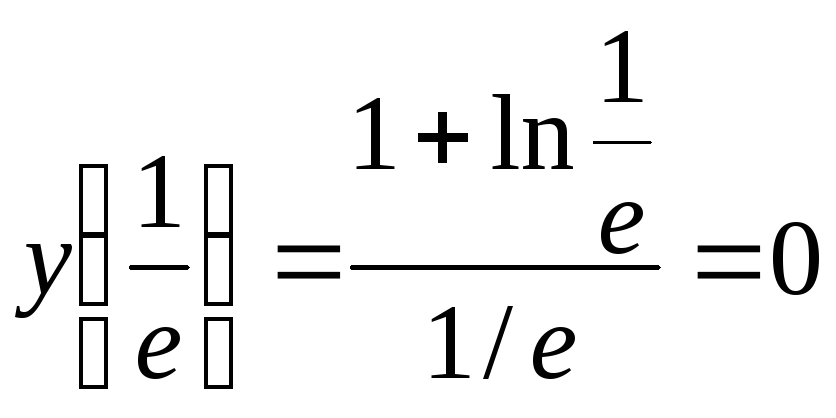Из полученных равенств следует, что наименьшее значение функции на отрезке равно , а наибольшее .

4)Провести полное исследование данной функции и построить ее график.

Решение.

Область определения функции .

В области определения функция является непрерывной, как частное двух непрерывных функций.

Т.к. односторонний предел , то прямая х = 0 является вертикальной асимптотой к графику функции.

Т.к. , то прямая у = 0 явлдяется горизонтальной асимптотой к графику функции и наклонных асимптот нет.

Найдем производную:

и приравняем ее к нулю

.

Для и, следовательно, функция возрастает, а для и, следовательно, функция убывает.

Значит в точке х = е функция достигает максимума равного

Найдем вторую производную:

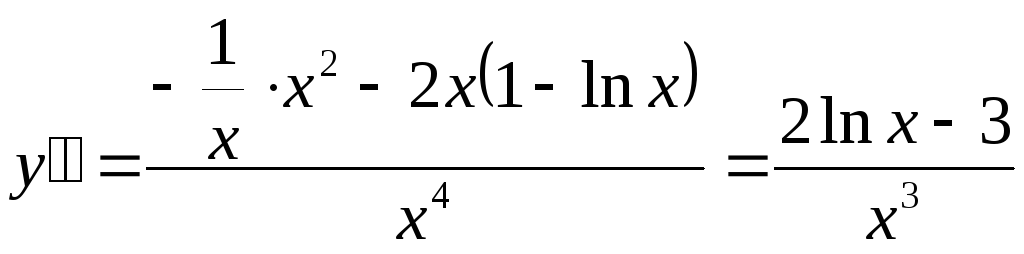
и приравняем ее к нулю

.

Для и, следовательно, функция выпукла вверх, а для и, следовательно, функция выпукла вниз.

Значит точка является точкой перегиба и

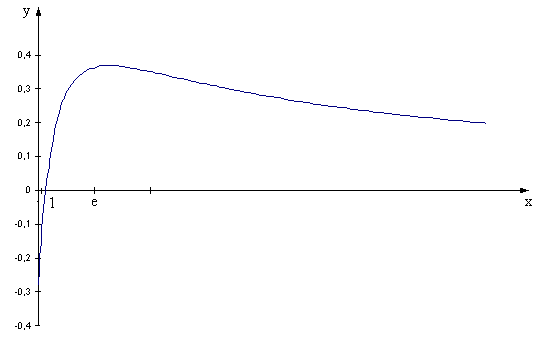
Сведем полученные данные в таблицу.

х		е
у	возрастает выпукла вверх	max	убывает выпукла вверх	т. перегиба	убывает выпукла вниз
	+	0	-		-
	-		-	0	+

По данным таблицы построим график:

5)Требуется изготовить открытый цилиндрический бак вместимостью V. Стоимость одного квадратного метра материала, из которого изготавливается дно бака, составляет а рублей, а стоимость одного квадратного метра материала, идущего на стенки бака, – b рублей. При каком отношении радиуса дна к высоте бака затраты на материалы будут минимальными?

Решение.

Пусть h – высота бака, а R – радиус его дна. Тогда стоимость дна будет равна , а стоимость стенки бака . Но бак имеет фиксированную вместимость V. Поэтому .

Следовательно, общая стоимость бака

.

Найдем производную этой функции

и приравняем к нулю. Получим

. Ясно, что при переходе через точку производная меняет знак с «-» на «+». Значит при этом значении R функция S(R) достигает минимума.

Найдем чему будет равно отношение радиуса дна к высоте бака. Т.к. 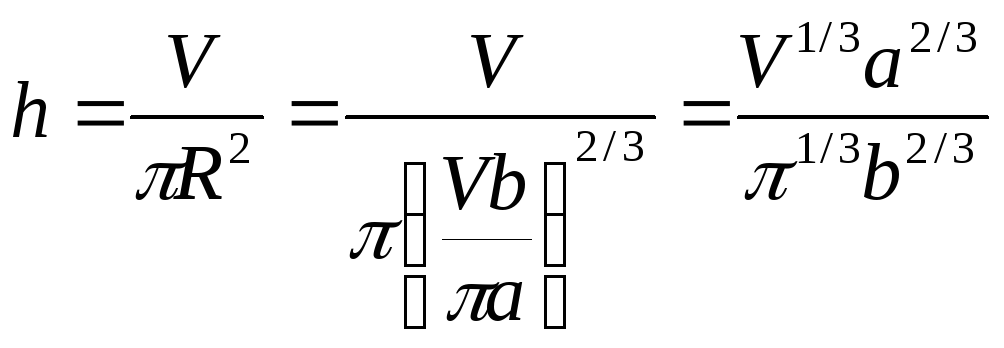, то .

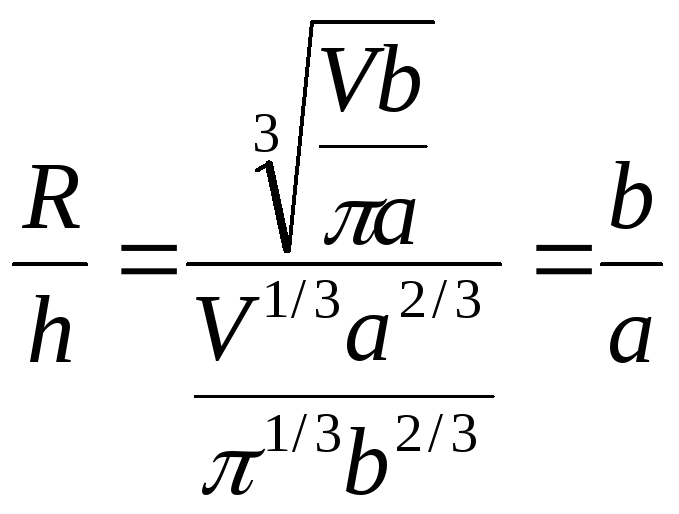Таким образом, затраты на материалы для бака будут минимальными при отношении радиуса дна к высоте бака равном .

31