КР 3, Вар 2

Контрольная работа № 3. Введение в математический анализ

Задачи 81–90

Выделив в заданной функции полный квадрат, получить уравнение параболы и построить её график.

Задача 82: .

Решение:

Выделим в заданной функции полный квадрат

Теперь применим метод преобразования координат. Известно, что график функции получают путем переноса графика вверх или вниз вдоль оси OY на в зависимости от знака b, график функции получается параллельным переносом графика при в положительном направлении оси ОХ на с, и в отрицательном направлении этой оси при , а график функции получается растяжением графика вдоль оси ОY в А раз при или сжатием вдоль этой оси в А раз при . Тогда график исходной функции можно построить, переместив вершину параболы в точку , перевернув ее ветвями вниз и затем растянув параболу в 4 раза вдоль оси OY.

Задачи 91–100

Задана функция на отрезке . Требуется: 1) построить график функции в полярной системе координат по точкам, давая аргументу значения через промежуток ; 2) найти каноническое уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить тип линии.

Задача  92: .

Решение:

1. Составим таблицу значений:

	0
r	1,20	1,24	1,36	1,59	2,00	2,69	3,78	5,21	1,20

6,00	5,21	3,78	2,69	2,00	1,59	1,36	1,24	1,20	6,00

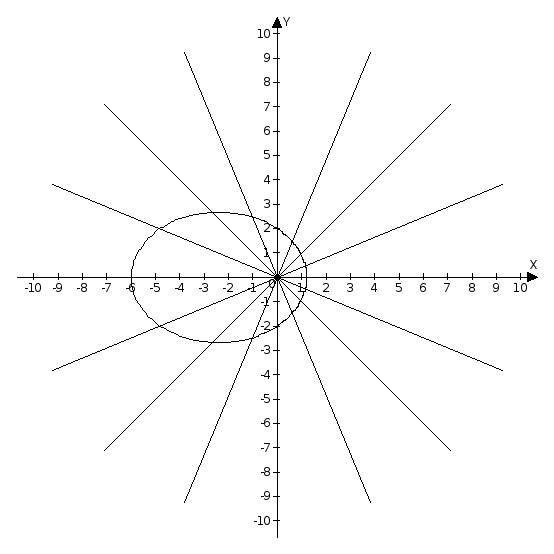
Для вычерчивания линии проведем радиусы-векторы, соответствующие углам , взятым с интервалом . На каждом из этих радиусов-векторов откладываем отрезки, равные значению r при соответствующем значении из таблицы . Соединяя точки, являющиеся концами этих отрезков, получаем график данной линии:

Задачи 101–110

Найти указанные пределы, не пользуясь правилом Лопиталя.

Задача 102: 1) ; 2) ; 3) .

Решение:

.

Задачи 111–120

Найти указанные пределы, используя эквивалентные бесконечно малые функции.

Задача 112: 1) ; 2) .

Решение:

.

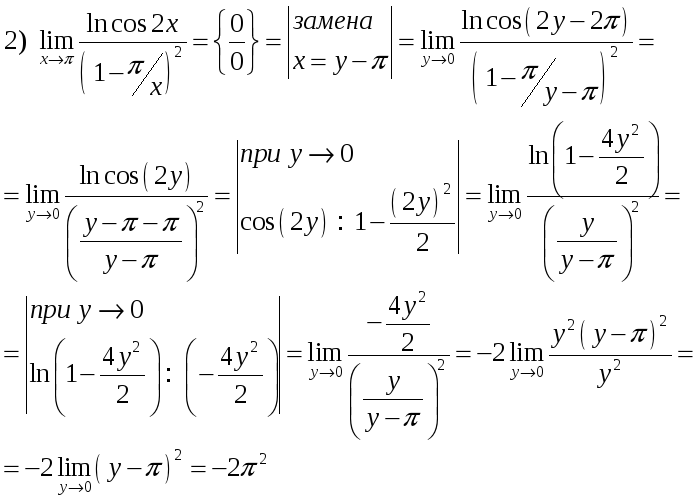Задачи 121–130

Задана функция различными аналитическими выражениями для различных интервалов изменения аргумента. Найти точки разрыва функции, если они существуют, и установить их тип. Сделать чертёж.

Задача 122: 

Решение:

Область определения функции f(x) – вся числовая ось. Разрывы возможны только в точках x = 0 и x = 4, в которых изменяется аналитическое задание функции.

Найдем односторонние пределы в точке x = 0 и значение функции в этой точке:

Следовательно, в точке x = 0 функция имеет разрыв 1-го рода, т.к. значение функции в этой точке не совпадает со значениями предела функции слева в этой точке.

Рассмотрим точку x = 4:

Так как односторонние пределы функции слева и справа конечны и равны значению функции в этой точке, то функция при х = 4 непрерывна.