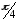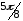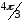К.р. №2 5 вариант
.docx|
|
|
|
|
|
|
|
|
Задача 75.Построить
график функции преобразованием
графика функции y
= sinx:
преобразованием
графика функции y
= sinx:
Решение
Произведём построение поэтапно:
1) построим
график ф-ции
2)построим
график ф-ции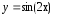 :для
этого произведём сжатие графика
:для
этого произведём сжатие графика
 вдоль
OXв 2раза
вдоль
OXв 2раза
3)построим
график ф-ции :
для этого произведём сдвиг графика
:
для этого произведём сдвиг графика
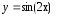 вдоль
OXвлево на 2.
вдоль
OXвлево на 2.
4)построим
график ф-ции :
для этого произведём сжатие графика
:
для этого произведём сжатие графика
 вдоль
OYв ¾раза. И отобразим
график зеркально
вдоль
OYв ¾раза. И отобразим
график зеркально

Задача 85.
Дана функция
 на
отрезке
на
отрезке
Требуется: 1) Построить график функции в полярной системе координат по точкам, давая φ значения через промежуток π/8 начиная от φ = 0; 2) найти уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить, какая это будет линия.
Решение
Составим таблицу значений:
|
|
0 |
|
|
|
|
|
|
|
|
|
r |
5 |
≈4,07 |
≈2,66 |
≈1,75 |
1,25 |
≈0,97 |
≈0,91 |
≈0,82 |
≈0,74 |
|
|
|
|
|
|
|
|
|
|
|
|
≈0,71 |
≈0,74 |
≈0,82 |
≈0,91 |
≈0,97 |
1,25 |
≈1,75 |
≈2,66 |
≈4,07 |
5 |
Для вычерчивания линии
проведем радиусы-векторы, соответствующие
углам
 ,
взятым с интервалом
,
взятым с интервалом
 .
На каждом из этих радиусов-векторов
откладываем отрезки, равные значению
r при соответствующем
значении
.
На каждом из этих радиусов-векторов
откладываем отрезки, равные значению
r при соответствующем
значении
 из таблицы . Соединяя точки, являющиеся
концами этих отрезков, получаем график
данной линии:
из таблицы . Соединяя точки, являющиеся
концами этих отрезков, получаем график
данной линии:

2. Подставляя
 и
и
 в уравнение заданной линии, получим
в уравнение заданной линии, получим



Полученное уравнение есть уравнение эллипса.
Задача 95. Найти указанные пределы, не пользуясь правилом Лопиталя:
а)
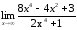 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)
 .
.
Решение
а) Подстановка
предельного значения аргумента приводит
к неопределённости вида
 .
Разделим числитель и знаменатель на
старшую степень аргумента, т.е. на
.
Разделим числитель и знаменатель на
старшую степень аргумента, т.е. на .
.
Получим
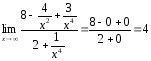 ;
;
так
как при
 функции
функции
 ,
,
 и
и
 – бесконечно малые функции.
– бесконечно малые функции.
б) Пределы
числителя и знаменателя при равны нулю, т.е. имеем неопределенность
равны нулю, т.е. имеем неопределенность
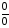 .
Избавимся от иррациональности в
числителе, домножив числитель и
знаменатель на
.
Избавимся от иррациональности в
числителе, домножив числитель и
знаменатель на
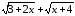 :
:


в) Применем 1-ый замечательный предел.
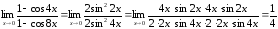
г)
Применим 2-ой замечательный предел.
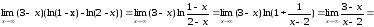

Задача 105.
Заданы функция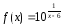 и
два значения аргумента
и
два значения аргумента
Требуется: 1)установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы при приближении к точке разрыва слева и справа; 3) сделать схематический чертеж.
Решение
Для
x=8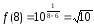 ;
; ;
функция непрерывна, т.к. ф-ция
определена и является элементарной.
;
функция непрерывна, т.к. ф-ция
определена и является элементарной.
Для
x=6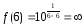 ф-циянеопределенна
и является разрывной
ф-циянеопределенна
и является разрывной
 ;
; 

Задача 115.
Задана функция
Найти точки разрыва функции, если они существуют. Сделать чертеж.
Решение
Очевидно, что
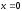 и
и
 являются точками, подозрительными на
разрыв, так как функция в них не определена.
В остальных точках функция непрерывна,
так как на каждом из интервалов
являются точками, подозрительными на
разрыв, так как функция в них не определена.
В остальных точках функция непрерывна,
так как на каждом из интервалов
 ,
,
 ,
,
 она определена и является элементарной.
она определена и является элементарной.
Вычислим односторонние
пределы
 в
подозрительных точках:
в
подозрительных точках:
 ;
; 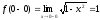 ;
;
 ;
; 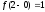 .
.
Поскольку
 то
то
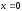 не
является точкой разрыва. В точке
не
является точкой разрыва. В точке
 функция имеет разрыв с конечным скачком,
так как
функция имеет разрыв с конечным скачком,
так как
 .
.

Построим график с учетом проведенного исследования.