К.р. №1 8 вариант

9

Искуственный

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ   Факультет непрерывного и дистанционного обучения Специальность: Искусственный Интеллект           КОНТРОЛЬНАЯ РАБОТА № 1 ПО ВЫСШЕЙ МАТЕМАТИКЕ Вариант № 8     Ф.И.О. Группа Зачетная книжка Электронный адрес:

Задание 8

Даны четыре вектора , , и , заданные в прямоугольной декартовой системе координат. Требуется:

1) вычислить скалярное произведение ;

2) вычислить векторное произведение ;

3) показать, что векторы образуют базис и найти координаты вектора в этом базисе.

Координаты векторов: ;;;.

Решение.

1. Вычислить скалярное произведение b (2a-c):

1.1.вычислим i=2a–c =2(-4;3;2) – (1;-6;-1) = (-9;12;5)

1.2. найдем скалярное произведение b * i =(0;5;3)*(-9;12;5) =

= 0*(-9)+12*5+3*5 =75

2) вычислим векторное произведение c*(a – 3b)

2.1. вычислим координаты вектора к =a – 3b = (-4;3;2) – 3*(0;5;3)=

=(-4;-12;-7)

i j k

2.2. Найдем векторное произведение = 1 -6 -1 = 30i–j(-11)+k(-36)=

-4 -12 -7

=(30;11;-36)

3) Покажем, что векторы a; b; c образуют базис и найдем координаты вектора d в этом базисе.

3.1. Найдем смешенное произведение векторов a; b; c, если оно не равно 0, то вектора a; b; c образуют базис.

-4 3 2

0 5 3 = -4 5 3 + 1 3 2 = -52-1 = -53 ≠ 0, значит a; b; c образуют базис.

1 -6 -1 -6 -1 5 3

3.2. Найдем координаты вектора d в базисе векторов a b c

d = αa+βb+γc данное равенство перепишем в виде системы и решим ее.

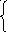-4α+0β+γ=-6 γ=4α-6 γ=4α-6 γ=4α – 6

3α+5β – 6γ=5 = 3α+5β – 6(4α-6)=5 = 5β-21α=-31 = 53α=53 =

2α+3β – γ=-2 2α+3β - 4α+6=-2 3β-2α=-8 3β – 2α=-8

γ=4α – 6 γ=-2

= α=1 = α=1

3β-2*1=-8 β= -2

d = 1a – 2b – 2c

Ответ: 1) скалярное произведение = 75; 2) векторное произведение = (30;11;-36); 3)вектора a;b;c образуют базис т.к. их произведение не равно 0, вектор d в этом базисе имеет координаты a – 2b – 2c.

Задание 18

Даны координаты вершин пирамиды . Найти: 1) длину ребра ; 2) уравнение прямой ; 3) угол между рёбрами и ; 4) уравнение плоскости ; 5) угол между ребром и гранью ; 6) уравнение высоты, опущенной из вершины на грань ; 7) площадь грани ; 8) объём пирамиды; 9) сделать чертёж.

Известно: ;;;.

Решение.

1) Найдем длину ребра А₁А₂.

Длина ребра А₁А₂ численно равна расстоянию между точками А₁и А₂, которое в прямоугольной декартовой системе координат вычисляется по формуле:

d =√ (x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²,

где x₂,y₂,z₂ – координаты точки А₂, x₁,y₁,z₁ – координаты точки А₁.

Таким образом, вычисляем:

d (А₁А₂) = √(4-6)²+5²+5² =3√6

2) Для составления уравнений прямой А₁А₂ воспользуемся формулой:

,

где x₀,y₀,z₀ – координаты точки А₁, x₁,y₁,z₁ – координаты точки А₂. Тогда уравнение прямой А₁А₂ имеет вид:

3) Угол между ребрами А₁А₂и А₁А₄ вычисляется по формуле:

,

где () – скалярное произведения векторов и.

Находим: =(-2;5;5); = = 3;

Находим: = (-5;1;5); = =;

* = (-2;5;5) * (-5;1; 5) = 10+(+5)+25 =40

= =

Следовательно =

4) Для составления уравнения плоскости A₁A₂A₃ воспользуемся формулой

=0,

где x₁, y₁, z₁ – координаты точки A₁; x₂, y₂, z₂ – координаты точки A₂; x₃, y₃, z₃ – координаты точки А₃.

=0 (x-6)* - (y – 1) * + (z-1) = =0

-10(x-6) – 12(y-1)+8(z-1)=0

5(x-6)+6(y-1)-4(z-1)=0

5x+6y-4z-32=0

5) Угол между ребром A₁A₄ и плоскостью A₁A₂A₃ определим по формуле:

= ,

где q– направляющий вектор прямой A₁A₄, то есть q = A₁A₄, а n – нормальный вектор плоскости A₁A₂A₃.

Из пункта 3 имеем q = A₁A₄ (-5;1;5), = =

n = = =

= i - j+ k = -10i – 12j+8k = 5i +6j – 4k n = (5;6;4)

= =

Таким образом,

=

Отсюда получаем, что = arc

6) Искомое уравнение высоты получим из канонических уравнений прямой: ==,

где М₁ (x₁,y₁,z₁) – точка, лежащая на искомой прямой; m, n, p – координаты направляющего вектора , параллельного искомой прямой. При этом в качестве точки M₀ возьмем точку A₄ (1;2;6), из которой по условию задачи должна быть опущена высота на плоскость A₁A₂A₃, а в качестве вектора возьмем нормальный вектор плоскости A₁A₂A₃, т.е. из пункта 5 вектор = (5;6;-4). Следовательно имеем следующее уравнение высоты .

7) Площадь грани A₁A₂A₃ находим, используя геометрический смысл векторного произведения:

=

Находим векторное произведение векторов :

= (-2;1;-1)

= = -10i – 12j + 8k

Таким образом, = =

8) Объем пирамиды A₁A₂A₃A₄ численно равен одной шестой модуля смешанного произведения векторов , которое находится по формуле:

( =

Таким образом, V = = *mod = = = 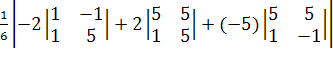(-12+40+50) = 13 уд³

9) Сделаем чертёж:

6

1

2 6

  1 А4

4 А3

А2

6

А1

Ответ: Ребро А₁А₂ =3 = уравнения плоскости A₁A₂A₃; 5x+6y-4z-32=0;= arc Площадь грани A₁A₂A₃ = ; Объем пирамиды A₁A₂A₃A₄ = 13 уд³.

Задание 28

 Найти координаты точки М', симметричной точке М (3;3;3) относительно плоскости 8x + 6y + 8z – 25 = 0.

Решение.

Запишем уравнение прямой перпендикулярной плоскости и найдем точку пересечения прямой и плоскости:

L:

= t x = 8t+3

= t y = 6t+3

= t z = 8t+3

Подставим эти уравнения в общее уравнение плоскости Р и получим

8(8t+3) + 6(6t+3) + 8(8t+3) = 25

64t+36t+64t = 25-24-18-24

164t = -41

t =-1/4

Подставив полученное значение параметра t =-1/4 в параметрические уравнения прямой L, получим координаты точки N = (1;1/2;1) – точки пересечения прямой L с плоскостью Р. Но так как N – середина отрезка MM', то

=1; =1/2; =1;

Отсюда:

x₂=-1

y₂=0

z₂=-1

Таким образом, точка М' имеет координаты (-1;0;-1).

Ответ: точка М' имеет координаты (-1;0;-1).

Задание 38

Составить уравнение линии, каждая точка которой равноудалена от точки А (4;2) и от оси ординат. Привести полученное уравнение к каноническому виду и указать тип линии, описываемой этим уравнением.

Решение.

Пусть М (х;у) любая точка искомой кривой и для нее выполнено условие точка равноудалена от А(4;2) и оси ординат F (0;y). Составим уравнение

=

=

Следовательно =(x – 4)²+(y – 2)² = x²

x=2+(y – 2)²/8

Данное уравнение это парабола с осью симметрии у = 2; в каноническом виде данное уравнение выглядит как (y – 2)² = 2 (4x-8).

у

А

М

х

Ответ: Данная кривая это парабола с осью симметрии у = 2; в каноническом виде уравнение данной параболы выглядит как (y – 2)² = 2 (4x-8).

Литература

1. Высшая математика. Общий курс /Под общ. ред. С.А.Самаля. Мн.:Вышейш. Шк., 2000.

2. Кузнецов А.В. Сборник задач и упражнений по высшей математике. Общий курс: Учеб. пособие. Мн.:Вышейш. Шк., 1994

3. Минюк С.А., Самаль С.А., Шевченко Л.И. Высшая математика для экономистов. Мн.: ООО «Элайда», 2003.

4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. I, II – М.: Высш. шк., 1980.