ВМ_КР5

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет заочного и дистанционного обучения

Специальность: Искусственный Интеллект

КОНТРОЛЬНАЯ РАБОТА

ПО ВЫСШЕЙ МАТЕМАТИКЕ №5

Вариант №5

№1

235. Дана функция 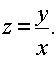Показать, что

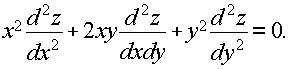
Решение

= –

=

= () = (– ) = 2

= () = () = –

= () = () = 0

Подставим , , в уравнение () + 2ху() + ()

(2 ) + 2ху(– ) + (0) = (2) – (2) + 0 = 0

№2

245. Дана функция z=f(x, y) и две точки А(х₀ , y₀) и В (х₁,_,y₁). Требуется: 1) вычислить значение z₁функции в точке В; 2) вычислить приближенное значение функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; оценить в процентах относительную погрешность, возникающую при замене приращения функции ее дифференциалом; 3) составить уравнение касательной плоскости к поверхности z=f(x, y) в точке С (x₀, y₀, z₀).

     А (1, 3),     В (0,96, 2,95).

Решение

1) Вычислим значение z₁функции в точке В :

= (0,96)² + 3(0,96*2,95) – (2,95)² = 0,9216 + 8.496 – 8.7025 = 0,7151

2) Вычислим приближенное значение:

= (1)² + 3(1*3) – (3)² = 1

= -0,04, = -0,05, z + df(A)

df(A) = +

= 2x + 3y, = 10

= 3x – 2y, = -3

z 1 + (10*(-0,04) + (-3)*(-0,05)) = 1 – 0,25 = 0,75

Относительная погрешность равна:

= *100% = *100% 4,9%

3) Уравнение касательной плоскости к поверхности z=f(x, y) в точке С (x₀, y₀, z₀):

z – z₀ = (2x₀ + 3y₀)(x-x₀) + (3x₀ – 2y₀)(y – y₀)

№3

255. Найти наибольшее и наименьшее значения функции в замкнутой области.

в прямоугольнике 0 x3, 0y4.

Решение

= y – 2

= x – 1

Найдем стационарные точки

y – 2 = 0, y = 2

x – 1 =0, x = 1

Точка (1,2) находится в области 0 x3, 0y4 , найдем значение функции в этой точке

z(1,2) = -2

x = 0, = -y, где y принадлежит [0;4], = -1, при любых y.

y = 0, = -2x, где х принадлежит [0;3], = -2, при любых x.

x = 3, = 2y – 6, где y принадлежит [0;4], = 2, при любых y.

y = 4, = 2x – 4, где х принадлежит [0;3], = 2, при любых x.

Найдем значения функции z в точках (0,0), (0,4), (3,0), (3,4)

z(0,0) = 0, z (0,4) = -4, z (3,0) = -6, z (3,4) = 2

Сравним значения z(0,0), z (0,4), z (3,0), z (3,4), z(1,2)

z_max = 2 в точке (3,4), z_min = -6 в точке (3,0)

№4

265. Дана функция z=z(x, y), точка A(x₀, y₀) и вектор а. Найти:

1) grad z в точке А; 2) производную в точке А в направлении вектора а.

     А (1, 1),     а = 6i - 8j .

Решение

1) grad Z(A) =

Найдем частные производные функции z в точке A

= 10xy + 3y² , = 13

= 5x² + 6xy , = 11

Тогда grad Z(A) =

2) Найдем производную в точке A в направлении вектора

Найдем единичный вектор вектора

= = – , где = = 10

Отсюда = ,

13* + 11* = = 16

№5

275. Найти формулу вида у=ах+b методом наименьших квадратов по данным опыта (таблицы)

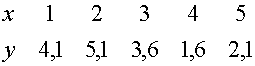
Решение

Система линейных уравнений для определения параметров а и b имеет вид

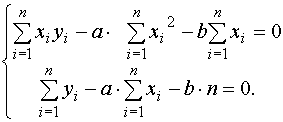
Составим таблицу

i	xi	yi	xi yi	xi2
1	1	4,1	4,1	1
2	2	5,1	10,2	4
3	3	3,6	10,8	9
4	4	1,6	6,4	16
5	5	2,1	10,5	25
	15	16,5	42	55

Система принимает вид

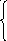
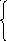
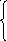
а = -0,75

b = 5,55

y = -0,75x + 5,55