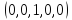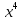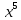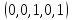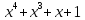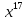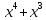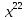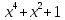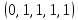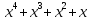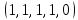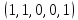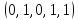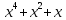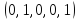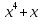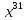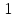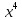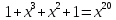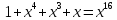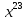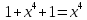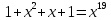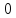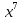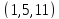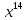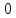Теория норм синдромов

Вариант 7.

Задание 1. Найти порождающую ( 21 * 31) -матрицу G по построенной в задании 7 из контрольной работы «Прикладная математика» для двоичной проверочной (10* 31) -матрицы H реверсивного-кода.

Решение

Прибавим к 2-ой строке 8-ю, к 3-ой строке – 5-ю, к 4-й строке – 6-ю, к 6-ой – 8-ю, к 7-ой – 10-ю, к 8-ой – 9-ю.

Прибавим к 1-ой строке 8-ю, ко 2-ой -4-ю , к 5-ой – 7-ю, к 9-ой – 8-ю и 4-ю, к 10-ой – 3-ю и 2-ю.

Прибавим ко 1-ой строке – 5-ю и 9-ю, к 3-ей – 5-ю и 9-ю, к 4-ой – 5-ю и 9-ю, к 5-ой – 9-ю, к 7-ой – 5-ю и 9-ю,к 8-ой – 10-ю и 9-ю, к 10-ой – 9-ю.

Прибавим к 2ой строке – 6-ю,8-ю,9-ю, к 4-ей –2-ю, 6-ю,8-ю,9-ю, к 8-ой –1-ю

Прибавим к 7-ой строке – 4-ю и 8-ю, к 3-ой строке – 4-ю,8-ю и 7-ю, к 9-ой строке –8-ю.

И переставим строки :

Базисный минор составляют первые 10 столбцов матрицы и базисными переменными являются переменные x1 , x 2 ,..., x10 . Поэтому свободными переменными являются x11 , x12 ,..., x31 . Положим x11= 1, x12= 0, ..., x31=0. Тогда базисные переменные принимают однозначно определенные значения, причем столбец этих значений ( x1 , x 2 ,..., x10) совпадает с первым столбцом подматрицы K матрицы . А в целом получим первый базисный вектор пространства решений и одновременно первый сттолбец матрицы G. И так находим остальные решения.

Порождающая матрица

Задание 2. С помощью найденной порождающей матрицы закодировать информацию

Задание 3. По найденному в задании 2 кодовому слову попытаться восстановить сообщение i.

В силу структуры матрицы G информационный вектор i идентично отображается на последние 21 координат вектора c и, следовательно, однозначно восстанавливается по вектору c . Т.е. имея , восстановим как последние 21 значение вектора :

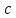Задание 4. По найденному в задании 8 синдрому из контрольной работы «Прикладная математика» найти вектор ошибок сведением задачи к квадратному уравнению и решением последнего по формулам Чэня.

Тогда:

Решим систему по формулам Чэня:

Уравнение:

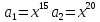
Значит ошибочными были позиции 16 и 21, а исправленное сообщение:

Задание 5. Для рассматриваемого в задании 4 кода данной контрольной работы составить таблицу образующих Г-орбит двойных ошибок, синдромов 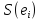и норм По синдрому из задания 8 в контрольной работе «Прикладная математика» найти вектор-ошибку норменным методом.

Решение

Воспользуемся таблицей:

Степенное задание	Полиномиальное задание	Векторное задание

Составим таблицу образующих Г-орбит двойных ошибок, синдромов и норм

Номер	Образующая	Синдром		Норма
1
2
3
4
5
6
7
8
9
10
11
12

Решим задачу норменным методом:

Следовательно, двойная вектор-ошибка e , которая присутствует в сообщении x , принадлежит Г-орбите 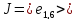и получается циклическим сдвигом вектора .

Найдем величину сдвига

Т.е. ошибка содержится на 16 и 21 позициях.

Задание 6. В (31, 16)-БЧХ-коде с проверочной матрицей 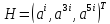, где 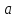корень примитивного полинома , принято сообщение с синдромом Найти вектор ошибок в принятом сообщении сведением задачи к кубическому уравнению и решением этого уравнения методом Чэня.

Решение

Составим систему:

Перейдем к элементарным симметрическим полиномам:

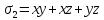
Составим новую систему:

Полученные значения 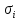служат, согласно теореме Виета, коэффициентами кубического уравнения 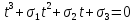, корнями которого и являются искомые неизвестные .

То есть ошибки расположены на 7-м, 15-м и 21-м местах.

Задание 7. Задачу из задания 6 решить норменным методом.

Решение

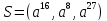
Определим вектора-ошибки, у которых первый синдром =0 :

#	вектор	S1	S2	S3	N
1
2
3
4
5	…	…	…	…	…

Нормы среди норм векторов тройной ошибки принадлежит вектору .

Вычислим сдвиг

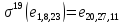
Это означает, что в сообщении ошибки на 15-м,21-м и 7-м местах.