
Контрольная №1
.doc
Задача 3.
Даны четыре вектора
![]() (а1,
а2,
а3),
(а1,
а2,
а3),
![]() (b1,
b2,
b3),
(b1,
b2,
b3),
![]() (c1,
c2,
c3)
и
(c1,
c2,
c3)
и
![]() (d1,
d2,
d3)
в некотором базисе. Показать, что векторы
(d1,
d2,
d3)
в некотором базисе. Показать, что векторы
![]() ,
,
![]() ,
,
![]() образуют
базис, и найти координаты вектора
образуют
базис, и найти координаты вектора
![]() в
этом базисе.
в
этом базисе.
![]() (-2,3,5),
(-2,3,5),
![]() (1,-3,4),
(1,-3,4),
![]() (7,8,-1),
(7,8,-1),
![]() (1,20,1).
(1,20,1).
Решение.
Базисом в пространстве
![]() являются
любые три некомпланарных вектора.
Условием компланарности трех векторов
является равенство их смешанного
произведения нулю. Итак, находим
являются
любые три некомпланарных вектора.
Условием компланарности трех векторов
является равенство их смешанного
произведения нулю. Итак, находим
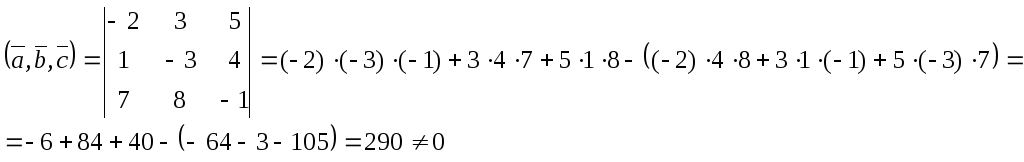
Значит, векторы
![]() некомпланарны
и образуют базис. Составим систему
уравнений в координатном виде
некомпланарны
и образуют базис. Составим систему
уравнений в координатном виде
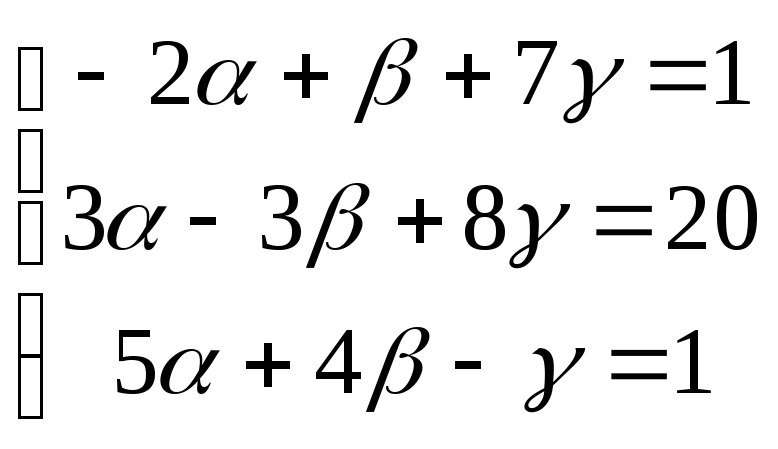 и найдем
и найдем
![]() .Определитель
Δ найден выше и Δ = 290.
.Определитель
Δ найден выше и Δ = 290.
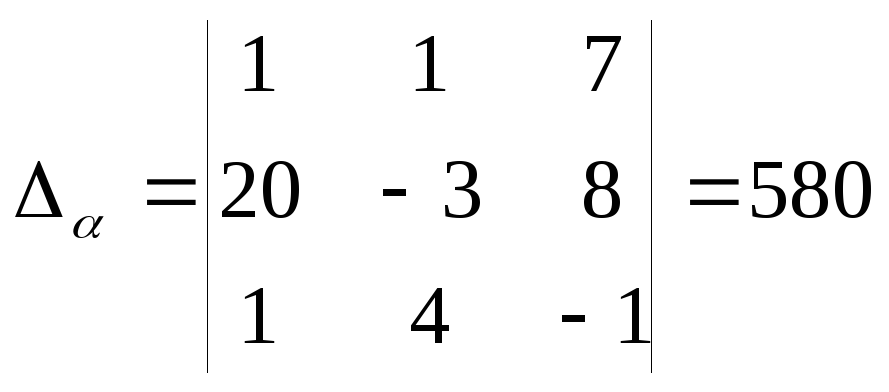 ,
,
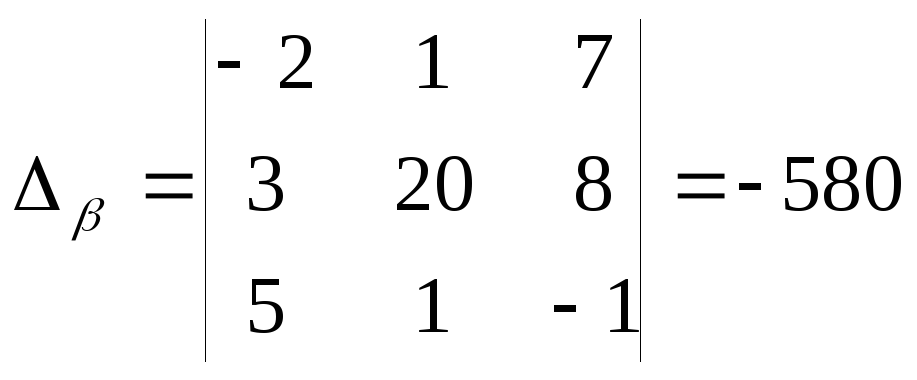 ,
,
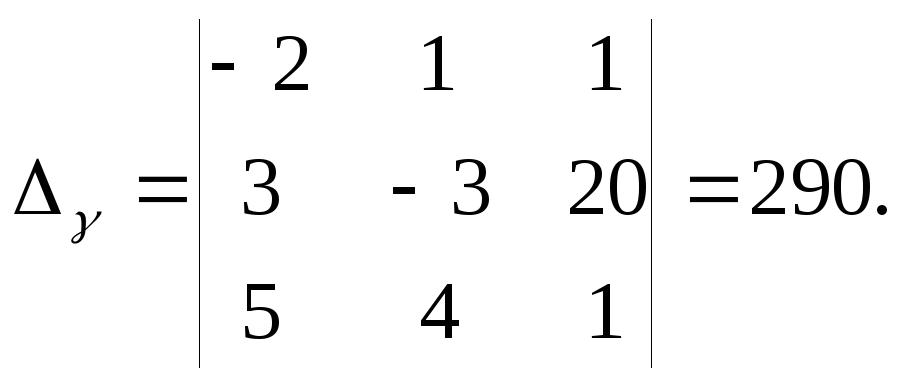
Имеем
![]() .
.
Значит
![]() .
.
Задача 13. Даны координаты вершин пирамиды A1A2A3A4. Найти: 1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4; 3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объём пирамиды; 6) уравнения прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнения высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертёж.
А1(3,5,4), А2(5,8,3), А3(1,9,9), А4(6,4,8).
Решение. 1. Находим координаты вектора
![]() и
длину ребра
и
длину ребра
![]() по
формуле (1.2).
по
формуле (1.2).
2. Угол между ребрами
![]() и
и
![]() вычисляется
по формуле
вычисляется
по формуле
![]() из
скалярного произведения.
из
скалярного произведения.
![]() ,
,
![]() ;
;![]()
![]() .
Поэтому
.
Поэтому![]()
![]()
3. Угол между ребром
![]() и
плоскостью
и
плоскостью
![]() -
это угол между вектором
-
это угол между вектором
![]() и
его ортогональной проекцией
и
его ортогональной проекцией
![]() на
грань
на
грань
![]() .
.
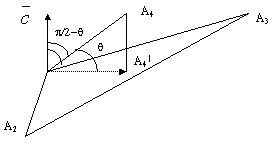
Вектор![]() перпендикулярен грани
перпендикулярен грани
![]() ,
что вытекает из определения векторного
произведения векторов
,
что вытекает из определения векторного
произведения векторов
![]() и
и
![]() (1.3):
(1.3):
 .
(Здесь
.
(Здесь
![]()
![]() Как и в предыдущем пункте, находим
Как и в предыдущем пункте, находим
![]()
![]()
4. Площадь грани
![]() находим,
используя геометрический смысл векторного
произведения
находим,
используя геометрический смысл векторного
произведения
![]() .
.
5. Объем пирамиды
![]() численно
равен одной шестой модуля смешанного
произведения векторов
численно
равен одной шестой модуля смешанного
произведения векторов![]() ,
,![]() ,
,![]() (формула 1.4).
(формула 1.4).
 .
.
6. Для составления уравнений прямой
![]() воспользуемся
формулой (1.7), где
воспользуемся
формулой (1.7), где
![]() -
координаты точки
-
координаты точки![]() ,
,
![]() -
координаты точки
-
координаты точки![]() .
.
![]() .
.
В таком виде уравнения прямой называются каноническими. Они могут быть записаны и в виде
 или
или![]() ,
т.е. уравнение прямой как линии пересечения
двух плоскостей.
,
т.е. уравнение прямой как линии пересечения
двух плоскостей.
7. Для составления уравнения
плоскости![]() воспользуемся
формулой (1.6), где
воспользуемся
формулой (1.6), где
![]() -
координаты
-
координаты![]() ,
,
![]() -
координаты
-
координаты![]() ,
,![]() -
координаты
-
координаты![]() .
.
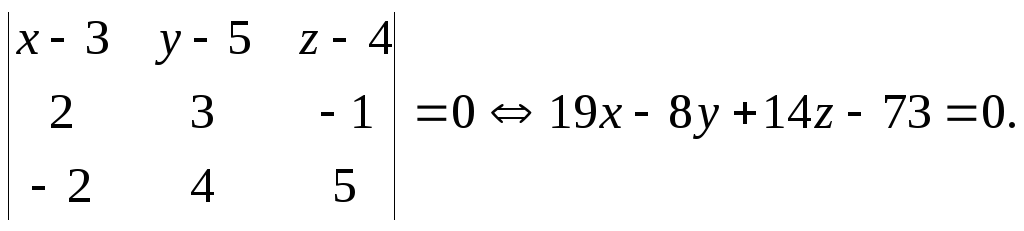
8. Искомые уравнения высоты получим из
канонических уравнений прямой
![]() ,
где
,
где
![]() -
точка, лежащая на искомой прямой;
-
точка, лежащая на искомой прямой;
![]() - координаты вектора
- координаты вектора
![]() ,
параллельного искомой прямой. При этом
в качестве точки
,
параллельного искомой прямой. При этом
в качестве точки
![]() возьмем
точку
возьмем
точку![]() ,
а в качестве вектора
,
а в качестве вектора
![]() возьмем
нормальный вектор плоскости
возьмем
нормальный вектор плоскости
![]() ,
т.е.
,
т.е.
![]() .
Имеем
.
Имеем
![]() .
.
9. Сделаем чертеж
A1
A3
A2
A4
x
0







Задача 23. Найти координаты точки, симметричной точке A(2,-4) относительно прямой 4x+3y+1=0.
Решение.
Нетрудно проверить, что координаты
точки А не удовлетворяют уравнению
прямой, т.е.
![]() .
.
Составим уравнение прямой
перпендикулярной прямой 4x+3y+1=0,
проходящей через точку A.
Запишем уравнение прямой в виде
![]() :
:
![]() .
Из условия перпендикулярности прямых
.
Из условия перпендикулярности прямых
![]() ,
уравнение прямой проходящей через точку
A(2;4)
и перпендикулярной прямой 4x+3x+1=0
будет иметь вид:
,
уравнение прямой проходящей через точку
A(2;4)
и перпендикулярной прямой 4x+3x+1=0
будет иметь вид:
![]() или
3x-4y-22=0.
или
3x-4y-22=0.
Найдем координаты точки N (точки пересечения прямых 4x+3y+1=0 и 3x-4y-22=0).
![]() .
.
Найдем координаты точки A1(x,y), зная координаты А (2,-4) и середину отрезка AA1, т.е. точку N(2,48;-3,64):
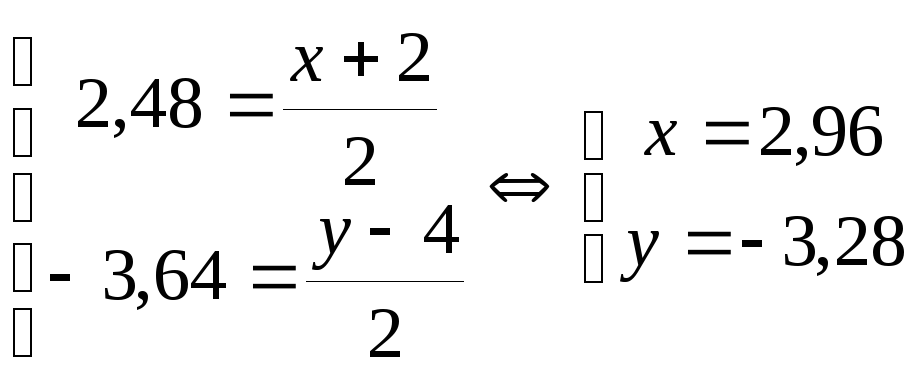 .
.
Задача 33. Построить на плоскости область решений системы линейных неравенств.
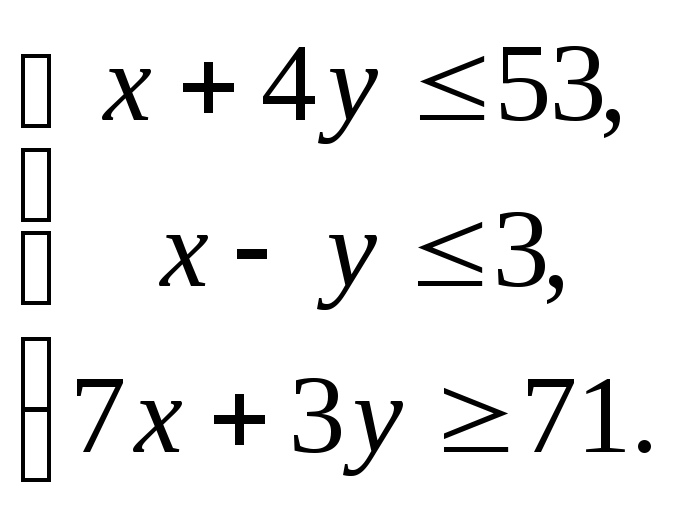
Решение. Чтобы решить неравенство
![]() ,
рассмотрим прямую
,
рассмотрим прямую
![]() .
Она проходит через две точки
.
Она проходит через две точки
![]() и
и
![]() .
При
.
При
![]()
B(5;12)
A(13;10)
C(8;5)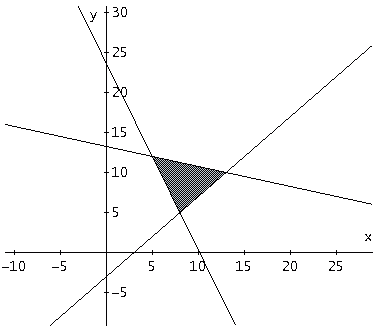
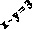

неравенство
![]() является
верным. Следовательно, ему удовлетворяют
все точки, лежащие ниже прямой
является
верным. Следовательно, ему удовлетворяют
все точки, лежащие ниже прямой
![]() и на прямой. Для решения второго
неравенства
и на прямой. Для решения второго
неравенства
![]() строим
прямую
строим
прямую
![]() ,
проходящую через точки
,
проходящую через точки
![]() и
и
![]() .
Точка
.
Точка
![]() удовлетворяет
неравенству
удовлетворяет
неравенству
![]() ,
следовательно, ему удовлетворяют все
точки, лежащие ниже прямой
,
следовательно, ему удовлетворяют все
точки, лежащие ниже прямой
![]() и
на этой прямой. Находим точку А
пересечения прямых
и
на этой прямой. Находим точку А
пересечения прямых
![]() и
и
![]() ,
решая систему
,
решая систему
![]() .
.
Наконец, решаем неравенство
![]() .
Для этого строим прямую
.
Для этого строим прямую
![]() ,
проходящую через точки
,
проходящую через точки
![]() и
и
![]() .
Точка (0;0) не удовлетворяет этому
неравенству
.
Точка (0;0) не удовлетворяет этому
неравенству
![]() ,
поэтому его решением является множество
точек плоскости выше прямой
,
поэтому его решением является множество
точек плоскости выше прямой
![]() и
на самой прямой.
и
на самой прямой.
Решая системы уравнений
![]() и
и
![]() ,
находим координаты точек
,
находим координаты точек
![]() и
и
![]() .
Данной системе неравенств удовлетворяют
все точки внутри треугольника АВС
и на его границе.
.
Данной системе неравенств удовлетворяют
все точки внутри треугольника АВС
и на его границе.
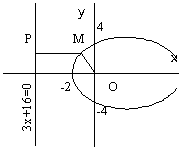
Задача 43. Составить уравнение линии, для каждой точки которой отношение расстояния до начала координат к расстоянию до прямой 3x+16=0 равно 0,6.
Решение. Обозначим произвольную
точку искомой линии
![]() .
Тогда по условию
.
Тогда по условию
![]() ,
где Р - основание перпендикуляра из
точки М к прямой
,
где Р - основание перпендикуляра из
точки М к прямой
![]() .
Но
.
Но
![]() ;
;
![]() .
Значит,
.
Значит,
![]() .
Возводя в квадрат, получаем
.
Возводя в квадрат, получаем
![]() .
Это каноническое уравнение эллипса с
полуосями
.
Это каноническое уравнение эллипса с
полуосями
![]() с
центром (3;0).
с
центром (3;0).
