Вышка 1 вариант 1 и 2 КР

1. Элементы линейной алгебры и аналитической геометрии

1. Даны векторы (a₁; a₂; a₃), (b₁; b₂; b₃), 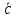(c₁; c₂; c₃) и (d₁; d₂; d₃) в некотором базисе. Показать, что векторы образуют базис, и найти координаты вектора в этом базисе.

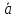(4;5;2), (3;0;1), (-1;4;2), (5;7;8).

Базисом в пространстве R³ являются любые три некомпланарных вектора. Условием компланарности трёх векторов является равенство их смешанного произведения нулю. Итак, находим:

= =

Значит векторы a,b,c некомпланарны и образуют базис. Составим систему

уравнений в координатном виде , и найдём

определитель найден выше ().

Имеем ;; .

Значит,

11. Даны координаты вершины пирамиды А₁А₂А₃А₄ .Требуется найти: 1) длину ребра А₁А₂; 2) угол между ребрами А₁А₂ и А₁А₄; 3) угол между ребром А₁А₄ и гранью А₁А₂А₃; 4) площадь грани А₁А₂А₃; 5) объём пирамиды; 6) уравнение прямой А₁А₂; 7) уравнение плоскости А₁А₂А₃; 8) уравнения высоты, опущенной из вершины А₄ на грань А₁А₂А₃; Сделать чертёж. А₁(3;1;4), А₂(-1;6;1),А₃(-1;1;6), А₄(0;4;-1)

1. Находим координаты вектора

И длину ребра

2. Угол между рёбрами и вычисляется по формуле из скалярного произведения ,

; ; ; (По таблице Брадиса)

3. Угол между ребром и гранью 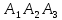– это угол вектором и его ортогональной проекцией на грань

Вектор перпендикулярен грани , что вытекает из определения векторного произведения векторов и

; (По таблице Брадиса)

4. Площадь грани находим, используя геометрический смысл векторного произведения:

5. Объём пирамиды численно равен одной шестой модуля смешанного произведения векторов , ,

6. Для составления уравнений прямой воспользуемся формулой

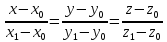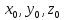, где – координаты точки , а – координаты точки

;

;

В таком виде уравнения прямой называются каноническими. Они могут быть записаны в виде 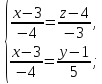или

т.е. уравнения прямой как линии пересечения двух плоскостей.

7. Для составления уравнения плоскости воспользуемся формулой уравнения плоскости, проходящей через три точки, которая имеет вид , где:

– координаты ;

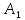– координаты точки ;

– координаты точки .

;

;

8. Искомые высоты получим из канонических уравнений прямой , где:

– точка, лежащая на искомой прямой;

m,n,p – координаты вектора , параллельного искомой прямой. При этом в качестве точки возьмём точку А₄(0;4;-1), а в качестве вектора – нормальный вектор плоскости , т.е. .

Имеем .

9. Сделаем чертёж:

21. Составить уравнение линии, каждая точка которой равноудалена от точки А(2;2) и оси абсцисс.

Пусть M(x;y) – произвольная точка искомой линии. Расстояние от точки M до оси абсцисс есть длина перпендикуляра MN, опущенного из точки M на ось. Определим координаты точки N. Очевидно, что ордината точки N равна 0, а абсцисса т.N равна абсциссе точки M, т.е. N(x;0). По условию задачи . Следовательно, для любой точки M(x;y), принадлежащей искомой линии, справедливо равенство MN=MA.

Тогда: , т.к. :

,

;

,

,

,

,

,

.

31. Доказать совместность данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.

А) При решении системы методом Гаусса действия производятся над строками расширенной матрицы

Б) Решим систему матричным способом:

Найдём алгебраические дополнения:

.

Отсюда следует, что

41. Найти размерность и базис пространства решений однородной системы линейных уравнений

Находим ранг основной матрицы с помощью элементарных преобразований:

,

Т.к. количество нулевых строк равно 1, а общее количество строк равно 3, то ранг матрицы равен: ;

Т.к. ранг системы меньше числа неизвестных, то система имеет ненулевые решения. Размерность пространства решений этой системы . Преобразованная система, эквивалентная исходящей, имеет вид:

Эти формулы дают общее решение. В Векторном виде его можно записать следующим образом:

Вектор-столбцы образуют базис пространства решений данной системы.

51. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матриц.

Составим характеристическое уравнение матрицы:

,

При , система имеет вид:

Таким образом, числу соответствует собственный вектор.

где – произвольное действительное число.

При имеем

Аналогично для имеем:

Второй собственный вектор

При , получаем собственный вектор

Для решаем систему:

Следовательно, собственный вектор

При , получаем собственный вектор

61. Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм

,

Левая часть уравнения представляет собой квадратичную форму с матрицей . Решаем характеристическое уравнение:

т.е.

По формуле:

Найдём собственные векторы из системы уравнений:

, при При система имеет вид

Таким образом, числу соответствует собственный вектор при имеем

При система имеет вид

Таким образом, числу соответствует собственный вектор при имеем

Нормируем собственные векторы (), получаем

…

2. Введение в анализ

71. Построить график функции преобразованием графика функции y=sin(x).

Записав данную функцию в виде замечаем, что в нашей функции ;

1. Строим одну волну синусоиды и отмечаем на ней несколько точек.

2. Увеличивая в 3 раза ординаты выбранных точек графика функции и оставляя неизменными абсциссы, затем, отображая полученную линию зеркально относительно оси ОХ, графика y=sin (x), строим график функции.

3. Увеличивая в 2 раза абсциссы точек графика функции и сохраняя неизменными ординаты, строим график функции .

4. Перенося точки графика функции в направлении оси абсцисс на 1 единицу масштаба этой оси вправо, строим искомый график функции .

81. Дана функция на отрезке . Требуется: 1) построить график функции в полярной системе координат по точкам, давая значения через промежуток , начиная от 2) найти уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить, какая это будет линия.

1)

φ	0	π/8	π/4	3π/8	π/2	5π/8	2π/3	3π/4	7π/8	π	9π/8	5π/4	11π/8	3π/2	13π/8	7π/4	15π/8	2π
r	∞	39,4	10,2	4,9	3	2,2	2	1,8	1,6	1,5	1,6	1,8	2,2	3	4,9	10,2	39,4	∞

2) Подставляя и в уравнение заданной линии, получаем

Это парабола с основанием в точке [-1.5;0]. Ветви направлены вправо.

91. Найти пределы функций, не пользуясь правилом Лопиталя:

а)

б)

в)

Воспользовавшись первым замечательным пределом, получаем:

г)

101. Дана функция 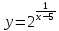и два значения аргумента х₁=3, х₂=2. Требуется: установить, является ли данная функция непрерывной или разрывной для каждого из данных значений х; 2) в случае разрыва функции найти ее пределы при приближении к точке разрыва слева и справа; 3) сделать схематический чертеж..

Функция в точке непрерывна, т.к. в этой точке пределы функции равны.

Точка есть точка разрыва, т.к. функция в этой точке не определена.

; ;

; ;

Чтобы схематически начертить график, найдём

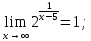
111. Задана функция y=f(x) различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать чертеж.

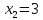Функция непрерывна на, функция непрерывна на , а функция непрерывна на , Значит, непрерывна на интервалах . Остаётся исследовать точки и . Находим левые и правые пределы функции в этих точках:

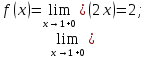
При функция имеет одинаковые односторонние пределы, значит, в этой точке функция непрерывна. Т.к. односторонние пределы при различны, функция в этой точке прерывна, а т.к. односторонние пределы конечны, то 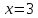является точкой разрыва 1-го рода.