
Высшая математика часть 1. Контрольная работа №3. Вариант 4
.docУЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет заочного, вечернего и дистанционного обучения
Специальность: программное обеспечение
информационных технологий
КОНТРОЛЬНАЯ РАБОТА
ПО ВЫСШЕЙ МАТЕМАТИКЕ № 3
Вариант № 4
3. ВВЕДЕНИЕ В АНАЛИЗ
Задание 104.
Построить график функции y = f(x) преобразованием графика функции y = sin x
y
= 2sin![]()
Для построения
графика функции y
= 2sin![]() воспользуемся
вспомогательными функциями:
воспользуемся
вспомогательными функциями:
-
y = sin x
-
y = sin

-
y = sin

-
y = 2sin

Все графики отобразим на одной системе координат:
-
y = sin x
x
0





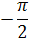
-
π
y
0

1
0
-
1
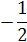
0
-
-
График y = sin
 получится из графика y
= sin
x
сжатием этого графика в коэффициентом
получится из графика y
= sin
x
сжатием этого графика в коэффициентом
 вдоль оси абсцисс. То есть значение
функции найдём при помощи
умножения
абсциссы на
вдоль оси абсцисс. То есть значение
функции найдём при помощи
умножения
абсциссы на  .
.
То есть
![]() *
* ![]() =
= ![]()
![]() *
* ![]() =
= ![]()
![]() *
* ![]() =
= ![]()
![]() *
* ![]() =
= ![]()
![]() *
* ![]() =
= ![]()
-
x
0



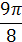


y
0

1
0
-
1

-
-
график y = sin
 получается из графика смещением точек
графика функции на 2 единицы влево в
системе x′0y′
и на
получается из графика смещением точек
графика функции на 2 единицы влево в
системе x′0y′
и на  * 2 =
* 2 =  в старой системе координат x0y.
в старой системе координат x0y. -
И в конечном итоге наш искомый график получится растягиванием графика функции y = sin
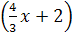 вдоль оси 0y
в 2 раза
вдоль оси 0y
в 2 раза

Задание 114.
Дана функция r = f(φ) на отрезке 0 ≤ φ ≤ 2π. Требуется:
1) построить график функции в полярной системе координат по точкам, давая j значения через промежуток p /8, начиная от j =0;
2) найти уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить, какая это будет линия.
r
= ![]()
-
Составим таблицу
|
φ |
0 |
|
|
|
|
|
|
|
π |
|
r |
2 |
~3,2 |
~6,8 |
~26,2 |
→∞ |
~26,2 |
~6,8 |
~3,2 |
2 |
|
φ |
|
|
|
|
|
|
|
2π |
|
r |
~1,4 |
~1,2 |
~1,04 |
1 |
~1,04 |
~1,2 |
~1,4 |
2 |

Подставляя r
= ![]() и sinφ
=
и sinφ
= ![]() в уравнение заданной линии, получим:
в уравнение заданной линии, получим:
![]() =
=  =>
=>
![]() = 2 + y
= 2 + y
![]() = 4 + 4y
+
= 4 + 4y
+ ![]()
![]() − 4y
– 4 = 0
− 4y
– 4 = 0
y
= ![]() – 1
– 1
Полученное уравнение есть уравнение параболы с вершиной в точке (0; −1)
Задание 124.
Найти указанные пределы, не пользуясь правилом Лопиталя.
а) ![]()
б) ![]()
в) ![]()
г) ![]()
а) ![]() =
= ![]() =
=  =
=  =
= ![]() =
= ![]()
б) ![]() =
= ![]() =
=  =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]()
в) ![]() =
= ![]() =
=  =
= ![]() =
= ![]()
г) ![]() =
= ![]() =
= ![]() =
=  =
=  =
= ![]() =
= ![]()
Задание 134.
Заданы функция y = f(x) и два значения аргумента x1 и x2.
Требуется:
1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента;
2) в случае разрыва функции найти ее пределы при приближении к точке разрыва слева и справа;
3) сделать схематический чертеж.
f(x)
= ![]() ,
, ![]() = 7 ,
= 7 , ![]() = 5
= 5
Функция в точке
![]() = 7 непрерывна, так как в этой точке
непрерывна функция
= 7 непрерывна, так как в этой точке
непрерывна функция ![]() , а также
, а также ![]() .
.
Точка ![]() = 5 – это точка разрыва этой функции, так
как f(x)
в этой функции не определена.
= 5 – это точка разрыва этой функции, так
как f(x)
в этой функции не определена.
 =>
=> ![]() = 5 – точка разрыва первого рода
= 5 – точка разрыва первого рода
Чтобы сделать схематический чертёж найдём:
![]() =
=  = 1
= 1

144. Задана функция y = f(x) различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать чертеж.
y
= 
Функция ![]() непрерывна на (−∞;
0], функция
непрерывна на (−∞;
0], функция ![]() непрерывна на (0; 2), а функция
непрерывна на (0; 2), а функция ![]() непрерывна на [2; +∞).
непрерывна на [2; +∞).
Значит функция
![]() непрерывна на
интервалах: (−∞; 0)
непрерывна на
интервалах: (−∞; 0)![]() (0;
2)⋃(2;
+∞).
(0;
2)⋃(2;
+∞).
Остаётся исследовать
точки ![]() = 0,
= 0, ![]() = 2. Находим левые и правые пределы в этих
точках:
= 2. Находим левые и правые пределы в этих
точках:
 =>
=> ![]() = 0 – это точка разрыва первого рода
= 0 – это точка разрыва первого рода
![]() = −1
= −1
 => в точке
=> в точке ![]() = 2 функция
= 2 функция ![]() непрерывна
непрерывна
![]() = 4
= 4

