
ВМ_КР6
.docУЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет заочного и дистанционного обучения
Специальность: Искусственный Интеллект
КОНТРОЛЬНАЯ РАБОТА
ПО ВЫСШЕЙ МАТЕМАТИКЕ №6
Вариант №5
№1
285. Найти неопределенные интегралы (результаты в случаях “а” и “б” проверить дифференцированием).
а)
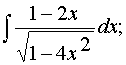 б)
б)
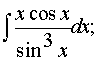 в)
в)
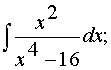
г)
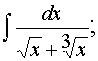 д)
д)
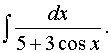
Решение
a)
![]()
![]() =
=
![]() –
–
![]()
Сделаем замену t = 2x, тогда
![]() –
–
![]() =
=
![]() –
–
![]() =
=
![]() –
–
![]() +
С
+
С
Рассмотрим
![]() :
:
Сделаем замену u = 1 – t2,
тогда du = -2t
dt, dt =
![]()
Следовательно
![]() =
=
![]() =
=
![]() =
=
![]() + C
+ C
Произведем обратную замену:
![]() +
C =
+
C =
![]() + C
+ C
Вернемся к
![]() –
–
![]() =
=
![]() +
+
![]() + C
+ C
Произведем обратную замену:
![]() +
+
![]() =
=
![]() +
+
![]() + C
+ C
Проверим результат:
![]() =
=
![]() =
=
![]()
б)
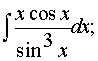
Сделаем замену u = x,
dv =
![]() .
Тогда du = dx.
Найдем v:
.
Тогда du = dx.
Найдем v:
v =
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() =
=
=
![]() + С
+ С
Используем интегрирование по частям:
![]() =
=
![]() =
=
![]() =
=
![]() + С
+ С
Найдем
![]() :
:
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() + С
+ С
Вернемся к
![]() =
=
![]() +
С =
+
С =
![]() + С
+ С
Проверим результат:
![]() =
=
![]() =
=
=
![]() =
=
![]() =
=
=
![]() =
=
![]() =
=
![]()
в)
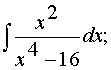
Воспользуемся интегрированием рациональных функций:
![]() - правильная рациональная дробь.
- правильная рациональная дробь.
Тк
![]() то
то
![]() =
=
![]() =
=
![]()
Приведем правую часть к общему знаменателю
(![]() ):
):
![]() =
=
![]()
![]() =
=
![]()
Приравняем коэффициенты при одинаковых степенях x:
![]()
![]()
![]()
![]()
Откуда С = 0, D =
![]() ,
A =
,
A =
![]() ,
B =
,
B =
![]()
Подставим найденные коэффициенты в разложение и проинтегрируем его:
![]() =
=
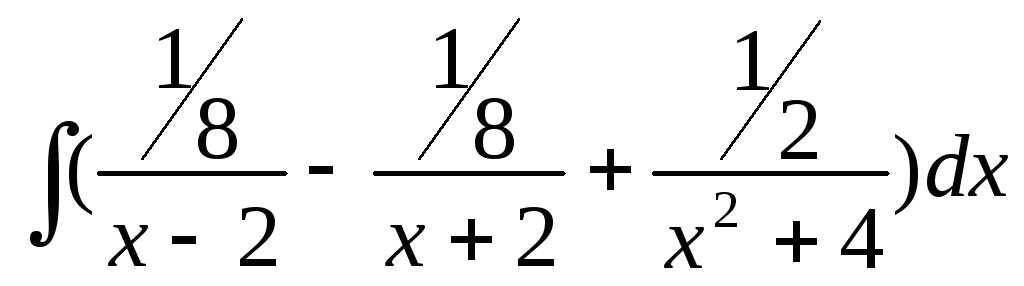 =
=
=![]() =
=
=![]()
г)
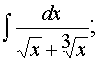
Используем подстановку
![]() ,
тогда
,
тогда
![]() ,
,
![]()
Следовательно
![]()
Выделив целую часть, получим:
![]() =
=
![]()
![]() +C
+C
Сделаем обратную подстановку:
![]() +C=
+C=
![]() +C
+C
д)
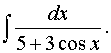
Используем подстановку
![]() ,
тогда
,
тогда
![]() ,
,
![]()
Следовательно
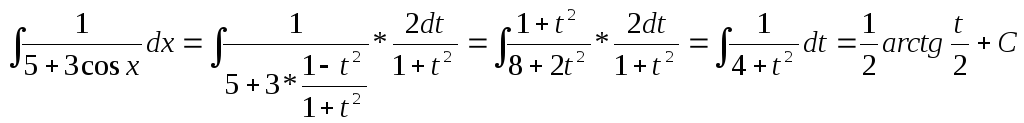
Сделав обратную подстановку, получим:
![]() =
=
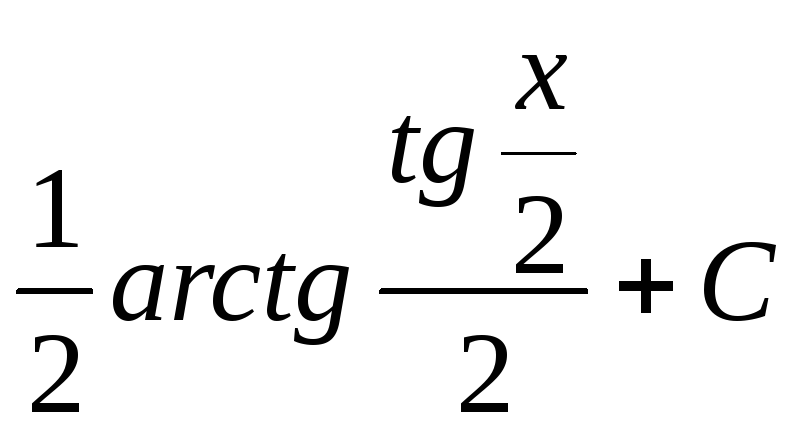
№2
295. Вычислить определенный интеграл. Окончательный результат представить в виде приближенного числа, произведя вычисление с округлением до третьего десятичного знака.
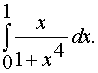
Решение
Пусть u = x2, тогда du = 2x dx =>
![]()
 =
=
![]() =
=
![]() =
=
![]()
![]()
![]() =
=
![]() (
(![]() –
–![]() )
=
)
=
![]() (
0,785 – 0)
(
0,785 – 0)
= 0,393
№3
305. Вычислить интеграл с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
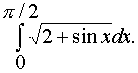
Решение
Поделим отрезок
![]() на десять равных частей:
на десять равных частей:
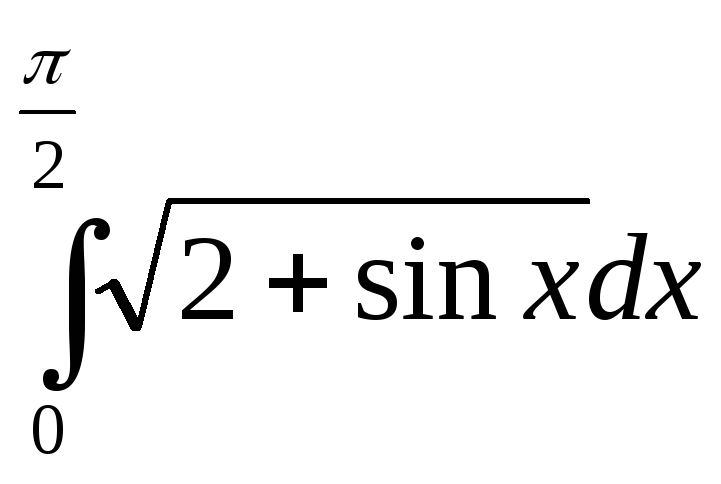
![]()
![]()
Вычислим значения функции:
![]() = y(0) = 1,414
= y(0) = 1,414 ![]() = y(
= y(![]() )
= 1,732
)
= 1,732
![]() = y(0,157) =1,468
= y(0,157) =1,468 ![]() = y(0,314) =1,519
= y(0,314) =1,519
![]() = y (0,471)=1,566
= y (0,471)=1,566 ![]() = y (0,628) =1,609
= y (0,628) =1,609
![]() = y (0,785)=1,645
= y (0,785)=1,645 ![]() = y(0,942) =1,676
= y(0,942) =1,676
![]() = y(1,099) =1,700
= y(1,099) =1,700 ![]() = y(1,256)= 1,718
= y(1,256)= 1,718
![]() = y (1,413)=1,728
= y (1,413)=1,728
Подставим полученные значения в формулу Симпсона:
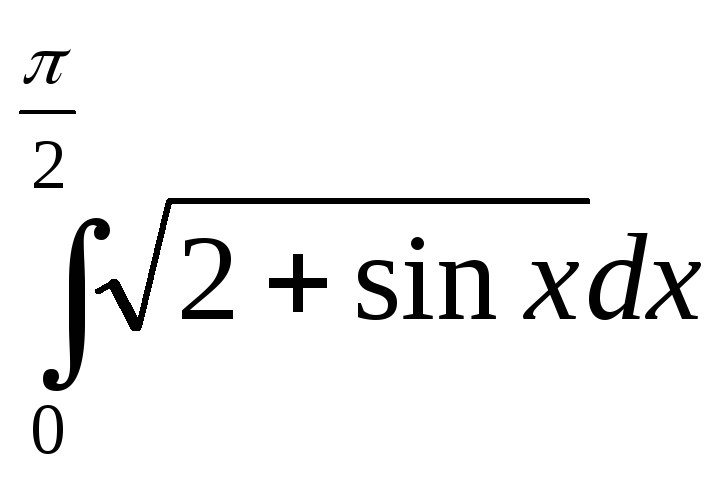
![]()
![]()
![]()
![]() 0,052*(3,146+32,428+13,044) = 2,528136
0,052*(3,146+32,428+13,044) = 2,528136
№4
315. Вычислить несобственный интеграл или доказать его расходимость.
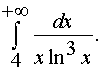
Решение
![]()
![]()
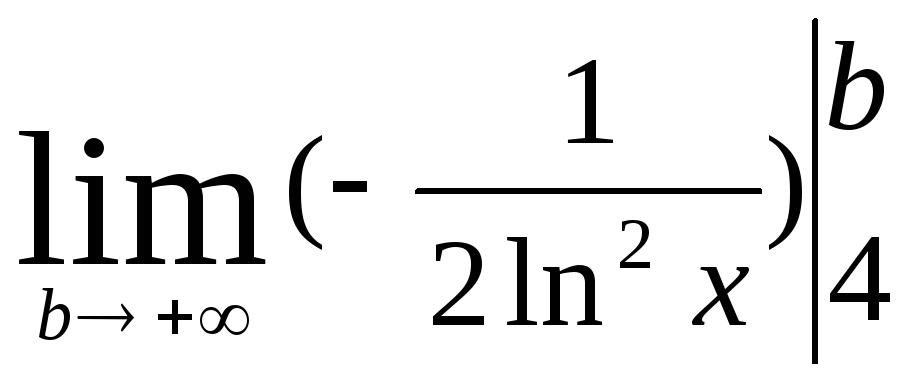 =
=
![]() =0,26
=0,26
Интеграл сходится.
№5
325. Вычислить площадь фигуры, ограниченной трехлепестковой розой r = 5 sin 3
Решение
Найдем область определения D(p):
![]()
При k = 0:
![]() и радиус вектор описывает один лепесток
и радиус вектор описывает один лепесток
При
![]()
![]()
Площадь всей фигуры будет равна 2*3 площади половины лепестка:
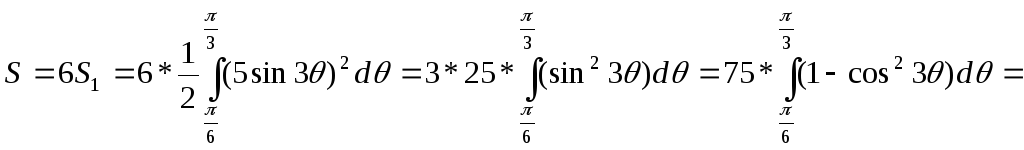
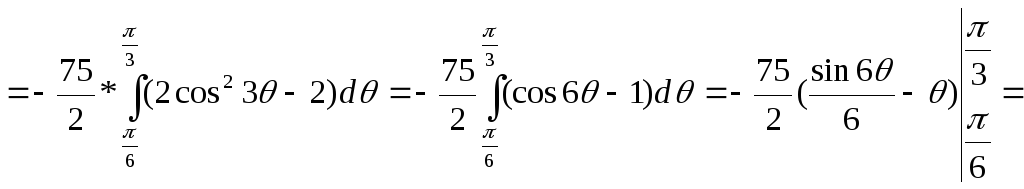
![]()
№6
335. Найти координаты центра тяжести
однородной дуги одной арки циклоиды
![]()
![]()
Решение
Координаты центра тяжести дуги равны
![]() ,
где
,
где
![]() равно верхнему пределу интегрирования
при котором длина дуги равна
равно верхнему пределу интегрирования
при котором длина дуги равна
![]() .
.
Найдем длину дуги:
L =
![]()
=
![]()
Т.к. функция
![]() периодична(
периодична(![]() ),
то
),
то
![]() =
=
![]() =
L
=
L
Также функция
![]() четная, следовательно
четная, следовательно
![]() =2
=2![]() = L
= L
![]()
Следовательно
![]()
Найдем x и y центра тяжести:
![]()
![]()
Координаты центра тяжести однородной дуги одной арки циклоиды (3.14;2)
