Основы линейной алгебры Вариант 7

Контрольная работа № 2. Основы линейной алгебры

Вариант 7

Задача 1.

Доказать совместность данной системы линейных уравнений и решить её тремя методами: 1) по формулам Крамера; 2) методом Гаусса; 3) средствами матричного исчисления (с помощью обратной матрицы).

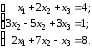
Решение

Система, имеющая хотя бы одно решение, называется совместной. Необходимым и достаточным условием совместности системы линейных уравнений является

Критерий Кронекера–Капелли. Для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу её основной матрицы. Если же эти ранги не равны, то система несовместна.

Составим расширенную матрицу системы для определения её ранга и ранга матрицы коэффициентов:

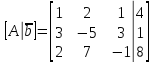
Находим ранг r расширенной матрицы:

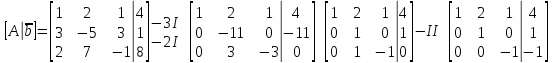
Отсюда 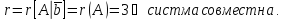Т.о. в системе трех уравнений три зависимые переменные.

1. Составим матрицу коэффициентов (основную матрицу системы) и найдем её определитель:

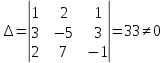
Так как определитель отличен от нуля, то система совместна и имеет единственное решение. Вычисляем определители

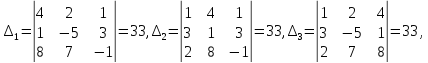
которые составляем из матрицы коэффициентов путем поочередной замены каждого из столбцов на столбец правой части системы.

Далее по формулам Крамера вычисляем:

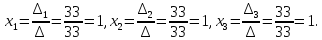
Таким образом, система имеет единственное решение

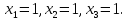
2. При решении системы линейных уравнений методом Гаусса действия производятся над расширенной матрицей. Эти действия были произведены при доказательстве совместности.

Т.о. система сводится к эквивалентной системе линейных уравнений

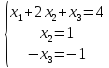
Откуда получим

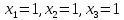
3. Определитель основной матрицы системы 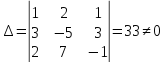, значит, система совместна и для матрицы коэффициентов существует обратная матрица. Находим решение по формуле 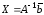или

,

где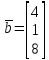, 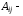алгебраические дополнения элементов 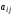матрицы А:

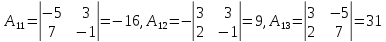
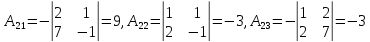
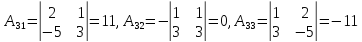
Таким образом, обратная матрица к основной матрице системы имеет вид

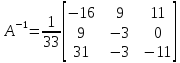
Значит, матричное решение системы имеет вид

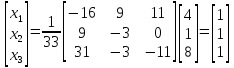
Отсюда следует, что

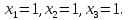
Задача 2.

Найти общее решение системы линейных уравнений.

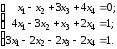
Решение

Проверим на совместность. Воспользуемся критерием Кронекера-Капелли(см. задачу 1) .

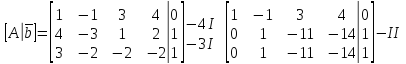
Отсюда получим, что 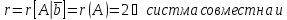в системе трех уравнений 2 зависимых переменных и 2 независимая. . Перенося слагаемые с x₃, х₄ в правую часть (базисный минор образован коэффициентами при х₁, х₂), по последней матрице записываем систему

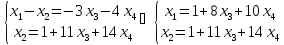
Итак, общее решение неоднородной системы линейных уравнений

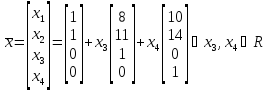
Задача 3.

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

Решение

Составляем характеристическое уравнение матрицы А и находим его корни:

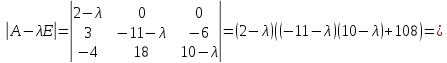
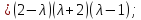
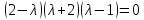
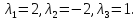
Так как все корни оказались действительными числами, то они являются собственными значениями матрицы А.

При 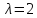система 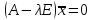имеет вид:

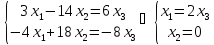
Значит, собственному значению 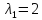соответствует собственный вектор

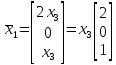
Здесь х₃ – произвольное действительное число, не равное нулю. Положив его, в частности, равным единице, получим собственный вектор в виде

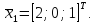
Аналогично при 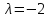система 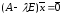имеет вид:

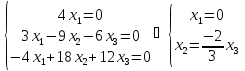
Значит, собственному значению 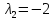соответствует собственный вектор

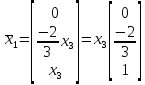
Здесь х₃ – произвольное действительное число, не равное нулю. Положив его, в частности, равным 3, получим собственный вектор в виде

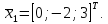
Аналогично при 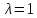система 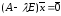имеет вид:

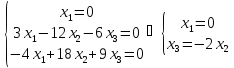
Значит, собственному значению 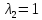соответствует собственный вектор

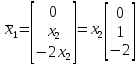
Здесь х₃ – произвольное действительное число, не равное нулю. Положив его, в частности, равным 1, получим собственный вектор в виде

Задача 4.

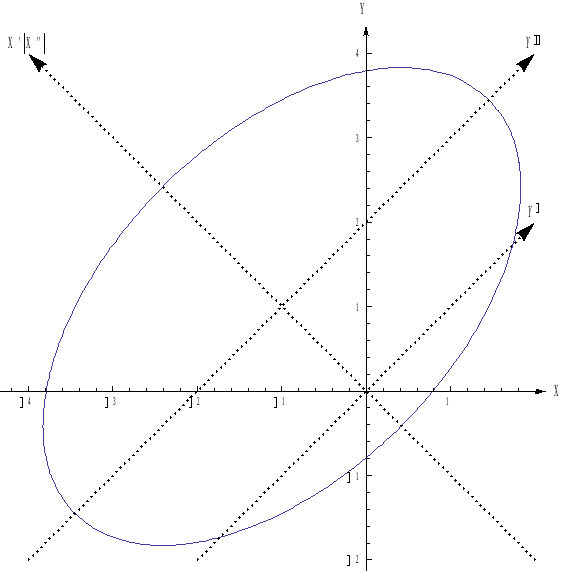
Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка и построить её в декартовой системе координат.

.

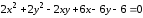Решение

В уравнении заданной кривой присутствует квадратичная форма следующего вида: 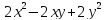. Составим матрицу данной квадратичной формы 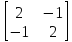и найдём её собственные значения:

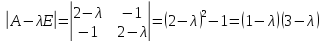
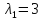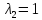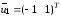Корнями характеристического уравнения являются числа и . Им соответствуют собственные векторы и .

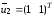Нормируя собственные векторы, получим

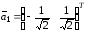и .

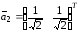Матрица перехода Т к новому базису имеет вид

.

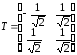В соответствии с соотношением 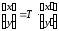вводим замену переменных

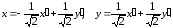
Подставим эти выражения в исходное уравнение кривой:

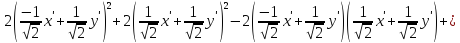
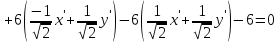
После преобразования выражения получим

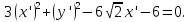
Или

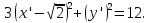
Введя замену 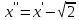получим уравнение эллипса.

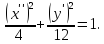
в системе координат . График полученного эллипса приведен на следующем рисунке.