К.р. №1 9 вариант

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОННИКИ

Факультет заочного и дистанционного обучения

Специальность: автоматизированные системы обработки информации

КОНТРОЛЬНАЯ РАБОТА

ПО ВЫСШЕЙ МАТЕМАТИКЕ №1

ВАРИАНТ №9

Электронный адрес:

Контрольная работа №1

Элементы векторной алгебры и аналитической геометрии

Вариант 9

№9

Даны четыре вектора ;;; в некотором базисе. Требуется: 1) вычислить скалярное произведение ; 2) вычислить векторное произведение ; 3) показать, что векторы образуют базис и найти координаты вектора в этом базисе.

Решение:

Так как скалярное произведение в ортонормированном базисе равно сум-ме произведений соответствующих координат, то

1) Скалярное произведение:

2) Векторное произведение:

3) Вычислим смешанное произведение векторов

Поскольку смешанное произведение этих векторов не равно нулю, то они не компланарны. Следовательно, они образуют базис.

Найдем координаты вектора в этом базисе:

№19

Даны координаты вершин пирамиды . Найти

1) Длину ребра ;

2) Уравнение прямой ;

3) Угол между ребрами и ;

4) Уравнение плоскости ;

5) Угол между ребром и гранью ;

6) Уравнение высоты, опущенной из вершины на плоскость

7) Площадь грани ;

8) Объем пирамиды;

9) Сделать чертёж;

; ; ; .

Решение:

1. Найдем координаты вектора :

.

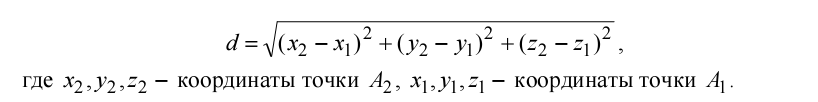
Длина ребра равна длине вектора :

.

2) Уравнение прямой :

.

3. Найдем координаты вектора :

.

Скалярное произведение векторов и равно:

.

Длина ребра равна длине вектора :

.

Тогда искомый угол равен:

3. Уравнение плоскости :

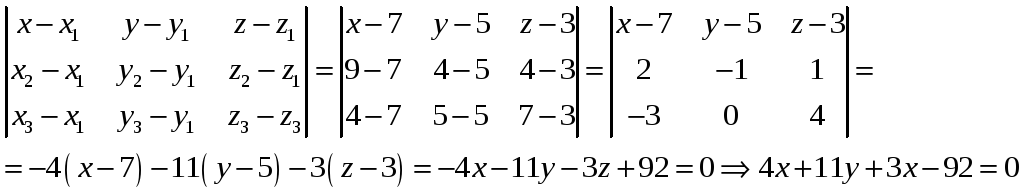
5) Угол между ребром и гранью :

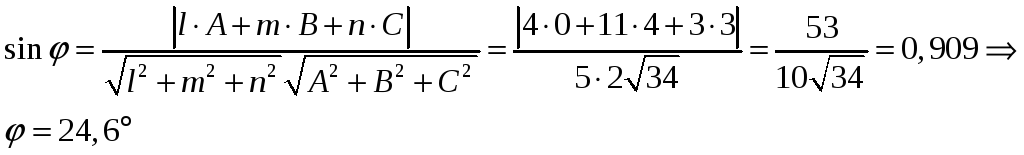
6) Направляющий вектор высоты, опущенной из вершины на плоскость , будет равен векторы нормали к плоскости :

.

Тогда уравнение этой высоты:

7) Найдем координаты вектора :

.

Площадь грани будет равно половине модуля векторного произведения векторов и :

8) Объем пирамиды будет равен одной шестой части модуля смешанного произведения векторов , и :

.

№29

Найти координаты точки , симметричной точке относительно прямой .

Решение:

Составим уравнение плоскости Р, проходящей через точку перпендикулярно прямой L, т.е. нормальный вектор Р есть :

.

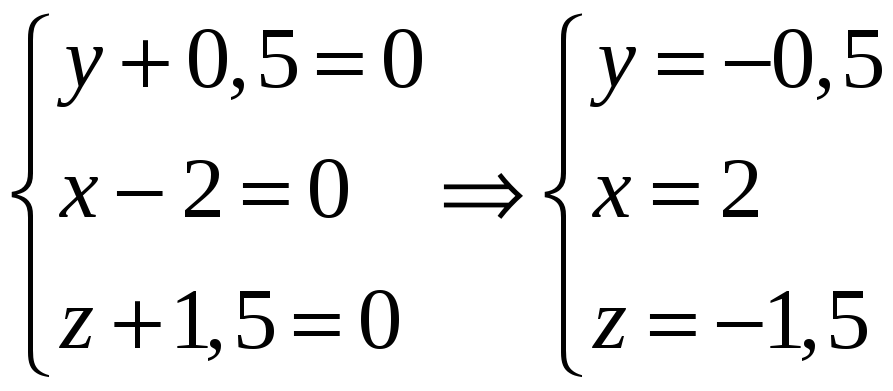
Решив совместно уравнения L и Р, получим точку N пересечения L с Р: . Но так как N –середина отрезка , то

.

Таким образом, точка имеет координаты .

№39

Составить уравнение линии, каждая точка которой отстоит от точки вдвое дальше, чем от прямой .

Решение:

Ответ: .

9) Сделать чертёж.