кр № 6 вариант 3

6. Кратные, криволинейные и поверхностные интегралы.

Элементы теории поля

263. Вычислить криволинейный интеграл вдоль окружности , обходя её против хода часовой стрелки.

273. Вычислить с помощью тройного интеграла объём тела, ограниченного указанными поверхностями. Данное тело и его проекцию на плоскость хОу изобразить на чертежах.

Сделаем чертёж проекции по плоскость xOy:

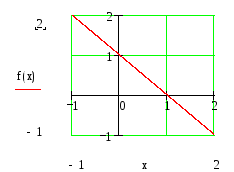
283. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах. Параметр а положителен.

Перейдём к полярным координатам:

293. Даны векторное поле  и плоскость Р:, которая совместно с координатными плоскостями образует пирамиду V. Требуется вычислить:

1) поток векторного поля F через часть плоскости Р, ограниченной координатными плоскостями, в том направлении нормали к плоскости Р, которая образует с осью Oz острый угол;

2) поток векторного поля F через полную поверхность пирамиды V в направлении внешней нормали к её поверхности.

1) Поток равен .

2) Поток по всей поверхности равен сумме модулей потоков через все четыре боковые поверхности. Поток через плоскость уже найдён, найдём потоки, проходящие через другие грани, которые являются координатными плоскостями.

При х=0 dx=0, тогда поток равен .

При у=0 dу=0, тогда поток равен .

При z=0 dz=0, тогда поток равен

Тогда поток через полную поверхность равен 37,333+0+0+2,667=40

310. Проверить является ли векторное поле F потенциальным и соленоидальным. В случае потенциальности поля найти его потенциал.

Для того, чтобы поле F было потенциальным нужно, чтобы .

Т.к. , значит, поле потенциально. Для нахождения потенциалов воспользуемся формулой:

Из первого уравнения , тогда .

Значит, – потенциал поля F.

Для соленоидальности поля необходимо и достаточно, чтобы .

Значит, поле F не соленоидально.