Контрольная №4
.docБелорусский Государственный Университет Информатики и Радиоэлектроники
Специальность:
Программное Обеспечение Информационных Технологий (ПОИТ)
Контрольная работа по математике №4
Вариант 1
Номер зачетной книжки 801021-21
Выполнил:
Мелещеня Валерий Сергеевич
151 Найти производную
данных
функций:
а)
б)
в)
г)
д)
Решение:
a)
y=
-
=
-
=
=
*
-
*
=
-
=
=
-
.
б)
=
=
=
=
=
=
=
.
в)
=
*
-
=
*
-
=
*(
-1)=
*
=
=-
.
г)
Возьмём как логарифмическую производную.
=
=
*
(
=
*
=
*
+
*
*
=-
*
+
*
=
*(-
+1)*y
=
*(1-
)*
.
д) x*sin y-y*sin x=0
Возьмём как производную сложной функции
=0
*sin
y+
*x-
*sin
x-
*y=0
Sin y+cos
y*
*x-
*sin
x-cos x*y=0
*(cos
y*x-sin x)=y*cos x-sin y
=
.
№ 161
Найти
и
а)
б)
Решение:
а) y=
*
=
=
-
+
*
=
*
-
*
=
=(
-
)*
=(
-
)*
=
*
=
*
.
=
=
=
*
+
*
=
*
-
*
=
*
-
*
=
*(
-
)=
=
*(
-
)=
*(
-
)=
*
=
*
б)
=
=1+
=1-
=1-tg
t
=1+
=1-
=1-ctg
t
=
=
=
=
=-tg
t.
=
=
=-
Тогда
=-
=-
=-
=-
.
№171 Применив
формулу Тейлора с остаточным членом в
форме Лангранжа к функции
вычислить
с точностью до 0,001 значения
и
.
Методом линейной интерполяции вычис-лить
приближенного значение
а=0,11, b=0,14, x0=0,12.
Решение:
Формула Тейлора для функции y=ex имеет вид:
=1+
+
+
+…+
+…
=1+
+
+
+…
Т.к.
=0,00022
0,001,
то для достижения необходимой точности
достаточно взять 3 первых члена разложения
в ряд:
=1+
+
=1+0,11+0,006=1,116
=1+
+
+
+…
=0,00046
0,001
Поэтому:
=1+0,14+0,010=1,150
Методом
линейной интерполяции находим 
.
По формуле:
y
+
(x-
),
где 
=0,11-наименьшее
известное значение аргумента
y(
)=
=1.116-соотв.
Значение функции
h=
-
=0.14-011=0.03
=
-
=0.150-0116=0.034
X=0.12
Значение
функции y=
в т. X=0.12
при этом:
1,116+
*(0,12-011)=1,116+0,011=1,127
Ответ:
=1.116,
=1.150,
=1.127.
№181 Найти наибольшее и наименьшее значения функции y=f(x) на отрезке [a,b].
Решение:
Находим
(x):
(x)=
=
=
=
=0
-
-12x+13=0
+12x-13=0
D=144-4*1*(-13)=196=142
=
=-13;
=
=1
-13
[-5;5];
1
[-5;5].
Находим f(1),f(-5),f(5):
f(1)=
=
=
f(-5)=
=
f(5)=
=
max
f(x)=
f(1)=
min
f(x)=
f(-5)=
Ответ: max
f(x)=
f(1)=
min
f(x)=
f(-5)=
№191 Сопротивление балки прямоугольного поперечного сечения на сжатие пропорционально площади этого сечения. Каковы должны быть размеры сечения балки, вырезанной из круглого бревна диаметром d , чтобы ее сопротивление на сжатие было наибольшим?
Решение:
Если сопротивление на сжатие пропорционально площади сечения, то, чем больше площадь, тем больше сопротивление. Значит из бревна заданного диаметра нам нужно получить балку (прямоугольного сечения) с наибольшей площадью.
Пусть тогда длина сечения - у, ширина – х.
Тогда S=x*y
Из
АВС:
у=
(по теореме Пифагора)
Тогда
S(x)=x*
Математически,
нужно найти максимум S(x)
на интервале [0;+
)
(из смысла задачи).
(x)=
+x*
=
+x*
*(-2x)=
=
-
-
=0
=0
=0
=
x=
Значит
при x=
S(x)
достигнет максимума. Значит, оптимальная
ширина: x=
, длина: y=
=
=
Ответ:
сечение должно быть x=y=
.
№201 Исследовать методами дифференциального исчисления функции и построить ее график, используя результаты исследования.
-
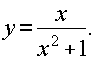
D(y)=
-
Функция не является периодической
y(-x)=
=
=-y(x)
Значит функция является чётной
-
Точки пересечения с осями – О(0;0)
-
Т.к. у(х) всюду непрерывна, то вертикальных асимптот нет.
Проверим наличие наклонной асимптоты:
y=kx+b
k=
=
*
=
=0
b=
=
=
=0
y=0
– горизонтальная
асимптота.
-
Найдём промежутки монотонности и точки экстремума.
=
=
=
=0
=0
-
+1=0
=1
x=
1
В т. x=-1 - минимум
В т. x=1 –максимум
y(-1)=
=
y(1)=
=
-
Находим промежутки выпуклости (вогнутости) и точки перегиба.
=
=
=
=
=
=
=
=
=
=0
=0
x=0,x=
В
точках x=0,
x=
– перегиб
y(0)=0;
y(3)=
=
y(-
)=
=
№211 Исследовать методами дифференциального исчисления функции и построить ее график, используя результаты исследования.
-
D(y)=(-
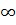;0)
(0;+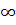
) -
Функция не периодическая
Т.к.
y(-x)=
y(x)
-y(x),
то функция не будет являться ни чётной,
ни не чётной.
3) Точки пересечения с осями:
C Ox:y=0
=0
=0
нет
решений – нет точек пересечения.
С Оу: - нет точек пересечения.
-
Исследуем поведение функции в окрестности точки х=0.