Высшая математика часть 2. Контрольная работа №4. Вариант 4
.docУЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет заочного, вечернего и дистанционного обучения
Специальность: программное обеспечение
информационных технологий
КОНТРОЛЬНАЯ РАБОТА
ПО ВЫСШЕЙ МАТЕМАТИКЕ № 4
Вариант № 4
4. ПРОИЗВОДНАЯ И ЕЁ ПРИЛОЖЕНИЯ
Задание 154. Найти
производную
данных функций.
а)
y′ =
(
)′
= 
* (
)′
= 
* (
=
= 
* 
* 
= 
= 
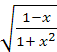б)
y′ = (tg
ln 
)′
= (tg 0,5 ln x)′ = 
* 0,5 * 
= 
в)
y′ =
(
)′
= ln 3 * 
* 2 cos x (− sin x) = − 2 ln 3 * 
*
* sin x cos x
г)
ln y = ln x * e −x
ln y = ln x + ln e −x
ln y = ln x + (− x) = ln x – x
= 
− 1
y = x * e −x
y´ = (1/x − 1) * x e −x
y´ = e –x – xe –x
д)
(cos(x – y) – 2x +4y) = (sin(x – y) + 4)
– sin(x – y) – 2 = 0
(sin(x –
y) + 4)
= sin(x – y) + 2
= 
Задание 164. Найти
и
а) 
y´
= 
= 
= 
= 
=
= − 
y´´
= − 
=
= − ( − 
(1 − 
+ 
* ( − 
(1 − 
) * ( − 2x)
) =
= 
– 
= 
– 
б) 
= 5
+ 2
= 3
+ 8
z
= y´
= 
= 
/ 
= 
= 
= 
Задание 174. Применив
формулу Тейлора с остаточным членом в
форме Лангранжа к функции
вычислить с точностью до 0,001 значения
и
.
Методом линейной интерполяции вычислить
приближенное значение
а=0,23, b=0,26, x0=0,24.
1 + x + 
+ … + 
x = 0.23: u0 = 1
u1 = 0.2300
u2
= 
= 0.0325
u3
= 
= 0.0020
u4
= 
= 0.0001
= 1.23 + 0.0325 + 0.0020 + 0.0001 = 1.2646 ≈ 1.265
x = 0.26: u0 = 1
u1 = 0.2600
u2
= 
= 0.0338
u3 = 
= 0.0029
u4 = 
= 0.0002
= 1.26 + 0.0338 + 0.0029 + 0.0002 = 1.2969 ≈ 1.297
= 
+ 
* (0.24 – 0.23) = 1.265 + 
* 0.01 = 1.265 + 
= 1.276
Задание 184. Найти
наибольшее и наименьшее значения функции
y=f(x)
на отрезке
[a,b].
f´(x) =
– cos x = 0
cos x = 
x = ± 
+ 2πn
x є [
π ; 2 π] => x = 
π
f (
π) = 
π + 1 ≈ 3.356
f (
π) = 
π + 
≈ 3.484 → max
f (2π) = π – 0 = π ≈ 3.14 → min
Задание 194. Из полосы жести шириной 11 см требуется сделать открытый сверху желоб, поперечное сечение которого имеет форму равнобочной трапеции. Дно желоба должно иметь ширину 7 см. Какова должна быть ширина желоба наверху, чтобы он вмещал наибольшее количество воды?
b
= 7
b + 2a = 11
a = 2
c - ?
Smax - ?
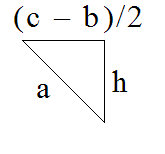
S = 
(b + c) * h
h = 
h = 
= 
= 
= 
S = 
(7 + c) 
= 
(7 + c) 
S´ = 
((7 + c) 
+ 
)
= 
(
)
=
=
* 
= 
* 
= 
= − 
− 
= 0
c1 =8; c2 = − 1
= 0
− (
− 14c + 33) = 0
− (c – 3)(c – 11) = 0
c3 = 3; c4 = 11
c = 8
Задание 204. Исследовать методами дифференциального исчисления функции и построить ее график, используя результаты исследования.
y
= 
= 
1. D(y) = (− ∞; 1) U (1; + ∞)
2.
y(−
x)
= 
= − 
=> не является чётной или нечётной
3.
y
= 0: 
= 0 => x
= 
4.
Точки разрыва: x
= 1, 
= ∞ => x
= 1 – вертикальная асимптота
Наклонные асимптоты:
k
= 
= 
= 0
b
= 
= 
= 0
y = 0 – горизонтальная асимптота
5. Возрастание / убывание
y´
= 
= 
= 
= 
x1 = 0; x2 = 1
6. Выпуклость / вогнутость
y´´
= (
)´
= 
= 
=
=
* ((1 − 2x)(x
− 1) – 4(x
– x2))
= 
* (x
– 2x2
– 1 + 2x
– 4x
+ 4x2)
=
=
(2x2
– x
– 1) = 0
2(x2
− 
x
− 
)
= 0
2(x
+ 
)(x
– 1) = 0
x1
= − 
;
x2
= 1
Задание 214. Исследовать методами дифференциального исчисления функции и построить ее график, используя результаты исследования.
1. D(y) = (− ∞; 0) U (0; + ∞)
2. y(− x) = 
= 
= 
− не является чётной или нечётной
3. y = 0 − нет
4. точки разрыва х = 0
= ∞ => вертикальная асимптота
k = 
= 
= 0
b = 
= 
= 0 => горизонтальная асимптота
5. y´ = (
)´
= − 
= 
= 0 => убывает на всём х
6. y´´
= − 
(
= − 
(
− 
(−
2(
)
* 
= − 
+ 
= 
+ 
= 
= 
=
= 
= 0
= 0
x = 0
Задание 224. Найти уравнение касательной и уравнение нормальной плоскости линии r = r(t) в точке t0 .
x
= 3
y
= t2
– t z = 3t3
+ t
x´
= 
y´
= 2t – 1 z´ = 6t + 1
x0 = 3 y0 = 0 z0 = 4
x´(t0)
= 
y´(t0)
= 1 z´(t0)
=7
Уравнение касательной:
= 
= 
= 
= 
=> 
= 
= 
Уравнение плоскости:
x´(f0)(x – x0) + y´(f0)(y – y0) + z´(f0)(z – z0) = 0
(x – 3) + 1y + 7(z – 4) = 0
x
+ y + 7z − 
= 0