
ВМ. Третья часть. Вариант 4
.docxУЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет заочного и дистанционного обучения
Специальность: «Искусственный интеллект»
КОНТРОЛЬНАЯ РАБОТА
ПО ВЫСШЕЙ МАТЕМАТИКЕ № 3
ВАРИАНТ № 4
Близнюк Виктор Иванович
Группа: 801721
Зачетная книжка: 602401-04
Электронный адрес: bliznuyk.victor@gmail.com
№344
xy' + y = sinx
y = u(x)·v(x)
y' = u'v + uv'
x·u'v + xuv' + uv – sinx = 0
v( xu' +u ) + xuv' – sinx =0
xu' + u = 0
 =>
ln
u = - ln
x
=>
ln
u = - ln
x
u = 1/x
xuv' – sinx = 0
v' – sinx = 0
dv = sinx dx
v = - cosx + e
peшение:
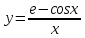
ответ:

№ 354
y''
- y'
= 9x – однородное уравнение, y(0)
= 0, y'(0)
= 1
– однородное уравнение, y(0)
= 0, y'(0)
= 1
λ² - λ = 0
 =
0
=
0
 = 1
= 1
Общее
решение y
=
 +
+

Частное решение ищем в виде:
 =
(Ax + B)
=
(Ax + B)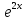
(y*)'
= A + 2
+ 2 (Ax
+ B) =
(Ax
+ B) =
 (2Ax
+ A + 2B)
(2Ax
+ A + 2B)
(y*)''
= 2A
4Ax + 4B + 4A – 2Ax – A – 2B = 9x
x | 2A = 9 => A=4,5
 |2B
+ 3A = 0 => B = -1,5A = -6,75
|2B
+ 3A = 0 => B = -1,5A = -6,75
y*
= (4,5x – 6,75)
y=
 +
+
 + (4,5x – 6,75)
+ (4,5x – 6,75)
используем начальные условия:
y(0)
=
 +
+

y'
=
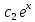 + 2(4,5x – 6,75)
+ 2(4,5x – 6,75) + 4,5
+ 4,5
y'(0)
=
 - 13,5 +4,5 = -5 =>
- 13,5 +4,5 = -5 =>


y
= 2,75 + 4
№ 364

 =
0 => λ² - 2λ – 3 = 0, λ1
=
3 , λ2
= -1
=
0 => λ² - 2λ – 3 = 0, λ1
=
3 , λ2
= -1
при λ1=3
-2γ1 +4γ2 = 0 γ1 = 2 γ2 γ2=с1
При λ2 = -1
2γ1 +4γ2 = 0 γ1 = -2 γ2
Общее решение – линейная комбинация полученных частных решений
x
= c1x1
+ c2x2
= 2c1 -
2c2
-
2c2
y
= c2y1
+
c2y2
= c1
 +
c2
+
c2
Ответ:
x=2c1 -
2c2
-
2c2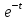
y=
c1
 +
c2
+
c2
|
v0 = 10 км/ч t1
=
v1 = 0.5 км/ч t2
=
F2 = 2v
|
|
|
|
|
vx - ?
по 2-ому закону Ньютона:
Fc = ma
αv
= ma,
a
=

 – обозначим
– обозначим
γv
=

γdt
=

γt
=
 => v=v0
=> v=v0
для t1
v1
= v0 =>
γ
=
=>
γ
=

для t2
vx
= v0
ex
( t2)
= 10 exp(
t2)
= 10 exp(
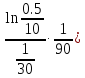 =
3.7 км/ч
=
3.7 км/ч
Ответ: vx = 3,7 км/ч
№384

A(1,2), B(3,5)
Первый отрезок: x = 1

Второй отрезок: y = 5

Ответ:
А = 42 +

№394
z=0; z=x²; 2x – y = 0; x + y = 9
V
=


Объем тела
V
=
 =
=
=

=

Ответ: V=526,5
№404
( x2 + y2)2 = a2( x2 + 2y2)
Перейдем к полярным координатам:
x =ρ cosφ; y = ρ sinφ
ρ4 = a2 ρ2 ( cos2φ + 2sin2 φ)
ρ2 = a2( 1 + sin2 φ)
ρ
= a
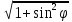
φ
S
=
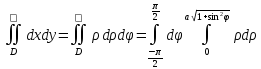 =
=
=
 =
=
 =
=
=
 a2
a2

 a2
a2 =
=
=
 (3φ
–
(3φ
–
 |
| =
=
 )=
)=

Ответ:
S =

№414
3x + 2y + 3z = 6
γ = x – плотность
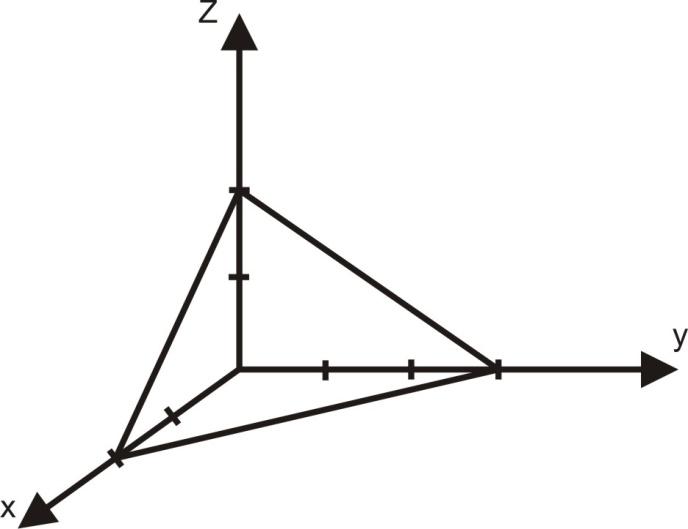
Найдем массу пирамиды
M
=
 =
=
=
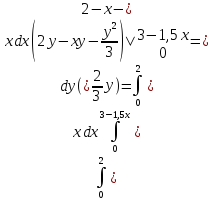
=

=

=
 =
=
=

№424
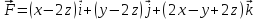
P: -x + 2y + 2z – 2 = 0


Поток
векторного поля: П =

z
= 1 +
 =
=
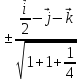 =
=

т.к. cos (n0, z)>0 , то n-n
n0
=
 ;
dδ
=
;
dδ
=
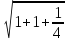 dxdy =
dxdy =

П
=
 =
=
 =
=
=

Ответ:
-

№434

Вычислим
rot

Поле потенциально:
U(x,y,z)
=
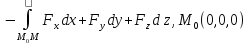
U(M)
=

Проверим соленоидальность поля
div
F
=

№444
 =
=

Исследуем сходимость ряда используя интегральный признак Коши
f(x)
=
 =
=
 (
(
 =
=
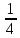
 =
=
 (
( - интеграл
сходится и значит там ряд сходится
- интеграл
сходится и значит там ряд сходится
Ответ: сходится
№ 454
 =
=

Область сходимости находим по принципу Даламбера:
R
=
 =
=
 =
=
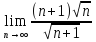 =
=

Область сходимости ряда вся числовая ось
x
Ответ:
x
№464

Разложим
 в
ряд Тейлора вблизи
в
ряд Тейлора вблизи

f(x)
= f(
sin
x²
= x²
-
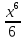 +
+
Так как отрезок интегрирования [0;1] находится внутри интервала сходимости данного ряда, то ряд можно почленно интегрировать
 =
=
=
 - то для заданной точности можно
ограничится первыми двумя членами ряда
=0,272
- то для заданной точности можно
ограничится первыми двумя членами ряда
=0,272
Ответ: 0,272
№ 474
y'
= 2
 -
xy
; y(0)
= 0
-
xy
; y(0)
= 0
Искомое решение ищем в виде ряда Тейлора:
Y
(x) = y (0) +
 +
+
 +……
+……
y'
(0) = 2 -
0·0 = 2
-
0·0 = 2
y''
= 2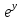 ·y'
– y - xy'
·y'
– y - xy'
y''(0)=
2 ·2
– 0 - 0·2 = 4
·2
– 0 - 0·2 = 4
y'''
= 2 (y')²
+ 2
(y')²
+ 2 y''
– 2y' - xy''
y''
– 2y' - xy''
y'''(0)
= 2 4
+ 2
4
+ 2 4
– 4 = 12
4
– 4 = 12
первые три члена ряда отличных от нуля:
y(x)
= 2x + 2x² +
 = 2x + 2x² +2x³
= 2x + 2x² +2x³
Ответ: y(x) = 2x + 2x² +2x³

 ч
ч ч
ч