Контрольная работа №5
.docx
215.
Дана функция
 .
Показать, что
.
Показать, что


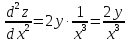





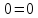
225.
Дана функция
 и две точки A(1;3)
и B(1,07;2;94).
Требуется:
и две точки A(1;3)
и B(1,07;2;94).
Требуется:
1)
Вычислить значение
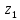 функции в точке B.
функции в точке B.

2)
вычислить приближенное значение
 в точке B
исходя из значения
в точке B
исходя из значения
 функции в точке А, заменив приращение
функции при переходе от точки А к точке
В дифференциалом.
функции в точке А, заменив приращение
функции при переходе от точки А к точке
В дифференциалом.


Итак






3)
составить уравнение касательной
плоскости к поверхности
 в точке
в точке








235. Исследовать на экстремум функцию двух переменных









Следовательно
в
 функция имеет минимум
функция имеет минимум

245.
Дана функция
 ,
точка А(1;1) и вектор
,
точка А(1;1) и вектор
 .
.
Найти
 в
точке А
в
точке А




2)
производную в точке А в направлении
вектора



где
 отсюда
отсюда


255. Найти условный экстремум при помощи функции Лагранжа
 при
при
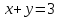








При
 ,
,
 ,
,
 ;
;

В этой точке условный максимум