Контрольная работа №3 (ВМ 4 часть АСОИ)
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Факультет непрерывного и дистанционного обучения
Специальность: Автоматизированные системы обработки информации
КОНТРОЛЬНАЯ РАБОТА
ПО ВЫСШЕЙ МАТЕМАТИКЕ №3
ВАРИАНТ №3
Группа
Зачетная книжка
Электронный адрес
563)Разложить
данную периодическую функцию с периодом
2 в
ряд Фурье на отрезке [-,].
Построить график суммы ряда, а также
графики первых частичных сумм
На отрезке [-,]
функция задана формулой.
Решение.
Найдем коэффициенты Фурье данной функции:
.
;
,
.
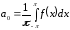
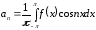
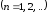Ряд
Фурье функции
:
в нашем случае будет иметь вид:
.
Т.к.
функция
непрерывна на интервалах
и
,
то ряд Фурье сходится к функции в каждой
точке этих интервалов. Поэтому знак «~»
можно заменить знаком «=», для
и
.
В точках
,
и
ряд сходится к среднему арифметическому
односторонних пределов функции в этих
точках, т.е.
Кроме того, т.к.
при n – четных и
при n – нечетных, то
ряд Фурье можно записать в виде:
.
Построим
график суммы ряда
.
Построим графики частичных сумм ряда.
573)Доопределяя необходимым образом, заданную в промежутке (0, а) функцию f(х), получить для нее: а) ряд Фурье по синусам; б) ряд Фурье по косинусам.
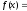
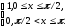
Решение.
а)
Доопределим функцию
до нечетной функции
.
Т.к. функция g(x) – нечетная, то коэффициенты ее ряда Фурье аn = 0. Найдем
.
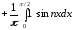
Тогда ряд Фурье по синусам функции g(x) будет иметь вид:
б)
Доопределим функцию
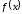до четной функции
.
Т.к. функция h(x) –четная, то коэффициенты ее ряда Фурье bn = 0. Найдем
;
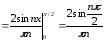(n
= 1, 2, …).
Тогда ряд Фурье по косинусам функции h(x) будет иметь вид:
.
Т.к.
при n = 2k
,
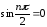а при n = 2k
-1
,
то этот ряд можно записать в виде:
.
583)Найти комплексную форму ряда Фурье периодической с периодом 2l функции f(х) и найти сумму полученного ряда в точке l, если:
Решение.
Найдем коэффициенты Фурье данной функции:
.
,
.
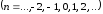Ряд
Фурье функции
:
в нашем случае будет иметь вид:
.
В
точке
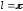периодическая функция равная
имеет разрыв. Поэтому ряд Фурье этой
функции сходится в этой точке к среднему
арифметическому односторонних пределов
функции
в этой точке, т.е.
.
593)Найти спектральную плотность S(ω) непериодического сигнала S(t), заданного формулой:
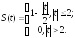
Решение.
Спектральную плотность S(ω) непериодического сигнала S(t) найдем по формуле преобразования Фурье:
.
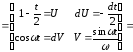
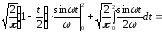
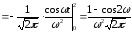599)Найти сигнал S(t) исходя из его спектральной плотности S(ω), если:
Решение.
Найдем сначала спектральную плотность функции
.
Найдем
;
.
Воспользуемся
обращением свойства преобразования
Фурье от n-ой производной:
если
,
то
.
При n = 2 получим
.
Таким образом сигнал S(t) соответствующий его спектральной плотности S(ω) будет равен:
.
603)
Методом Фурье найти уравнение u=u(x,t)
формы однородной струны для любого
момента t, если струна закреплена на
концах х=0
и х=l и
в начальный момент t=0
форма струны и скорость точки струны с
абсциссой х
определяются соответственно заданными
функциями
Решение.
Уравнение колебания струны имеет вид:
.
Его
решение будем искать в виде
при граничных условиях:
Тогда X(0) = X(l) = 0.
Подставим решение в исходное уравнение:
.
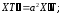
Т.к. левая часть последнего уравнения зависит только от t, а правая только от х, то заключаем, что
.
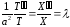Решаем
дифференциальное уравнение
.
Составим для него характеристическое
уравнение
.
Чтобы удовлетворить начальным условиям
X(0) =
X(l)
= 0 необходимо, чтобы
.
Тогда общее решение этого дифференциального
уравнения будет иметь вид:
.
Тогда
;
Таким образом, функция Х имеет вид:
Аналогично находится функция T(t):
Все решения исходного дифференциального уравнения, удовлетворяющие граничным условиям, можно записать в виде:
Окончательно решение уравнения колебаний струны можно записать в виде:
где
.
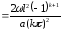
Таким образом, окончательное решение уравнения колебаний струны можно записать в виде:
