Вырожденное распределение

Говорят, что случайная величина имеет вырожденное распределение в точке , и пишут: , если принимает единственное значение   с вероятностью 1, т.е. . Функция распределения имеет вид:

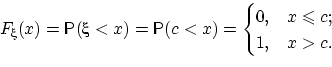
Распределение Бернулли

Говорят, что случайная величина имеет распределение Бернулли с параметром , и пишут: , если принимает значения 1 и 0 с вероятностями и соответственно. Случайная величина с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха : ни одного успеха или один успех. Таблица распределения имеет вид:

	0	1

Функция распределения случайной величины такова:

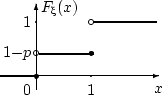
Биномиальное распределение

Говорят, что случайная величина имеет биномиальное распределение с параметрами и , и пишут: , если принимает значения с вероятностями . Случайная величина с таким распределением имеет смысл числа успехов в испытаниях схемы Бернулли с вероятностью успеха . Таблица распределения имеет вид:

Распределение Бернулли совпадает с распределением  .

Распределение Пуассона

Говорят, что случайная величина имеет распределение Пуассона с параметром , где , и пишут: , если принимает значения с вероятностями  .

Геометрическое распределение

Говорят, что случайная величина имеет геометрическое распределение с параметром , и пишут , если принимает значения с вероятностями . Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха  . Таблица распределения имеет вид:

Равномерное распределение

Говорят, что имеет равномерное распределение на отрезке , и пишут: , если плотность распределения постоянна на отрезке и равна нулю вне него:

Очевидно, что площадь под графиком этой функции равна единице и  . Поэтому  является плотностью распределения.

Случайная величина имеет смысл координаты точки, выбранной наудачу на отрезке . Вычислим по определению 30 функцию распределения случайной величины :

Получим следующую непрерывную функцию распределения:

Показательное распределение

Говорят, что имеет показательное (экспоненциальное) распределение с параметром , и пишут: , если имеет следующую плотность распределения:

   

Функция распределения случайной величины непрерывна:

Показательное распределение является единственным абсолютно непрерывным распределением, для которого выполнено свойство «нестарения» (и в этом смысле оно является непрерывным аналогом дискретного геометрического распределения).

Гамма-распределение

Говорят, что имеет гамма-распределение с параметрами , , и пишут: , если имеет следующую плотность распределения:

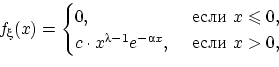
где постоянная вычисляется из свойства (f2) плотности так:

откуда . Здесь через обозначен интеграл

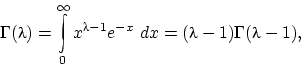
называемый гамма-функцией Эйлера⁽³⁾; при целых положительных , . Замена в интеграле Пуассона даст .

Показательное распределение — частный случай гамма-распределения: .