1. Определения: пространство элементарных исходов, сигма-алгебра событий, вероятностная мера. Свойства вероятности, вытекающие из аксиом.

Пространством элементарных исходов называется множество, содержащее все возможные результаты данного случайного эксперимента, из которых в эксперименте происходит ровно один. Элементы этого множества называют элементарными исходами и обозначают буквой («омега»).

---------------------------------------------------------------------------------------------------------------------

Множество , элементами которого являются подмножества множества (не обязательно все) называется -алгеброй ( -алгеброй событий), если выполнены следующие условия:

1)      ( -алгебра событий содержит достоверное событие);

2)  если , то (вместе с любым событием -алгебра содержит противоположное событие);

3)  если ,  , то (вместе с любым счётным набором событий -алгебра содержит их объединение).

--------------------------------------------------------------------------------------------------------------------

Пусть — пространство элементарных исходов, — -алгебра его подмножеств (событий). Вероятностной мерой на называется функция , обладающая свойствами:

(P1) для любого события выполняется неравенство ;

(P2) для любого счётного набора попарно несовместных событий имеет место равенство

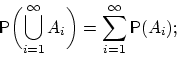
(P3) вероятность достоверного события равна единице: .

-----------------------------------------------------------------------------------------------------------------

Свойства (P1) — (P3) называют аксиомами вероятности. Из аксиом вытекает:

Свойство 0.   .

Свойство 1.  Для любого конечного набора попарно несовместных событий имеет место равенство

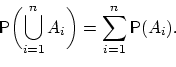
Свойство 2.  Для любого события выполнено: .

Свойство 3.  Если , то .

Свойство 4.  Если , то .

Свойство 5.  Для любого события выполнено: .

Свойство 6.  Всегда .

Свойство 7.  Всегда .

Свойство 8.  Совершенно всегда .

Свойство 9.  Для любого конечного набора событий , , имеет место равенство:

2. Классическое определение вероятности. Основные комбинаторные формулы: Cnk, Ank, nk – что они вычисляют.

Предположим, что мы имеем дело с пространством элементарных исходов, состоящим из конечного числа элементов: .

Если событие состоит из элементарных исходов, то вероятность этого события равняется отношению :

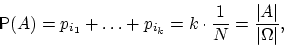
Говорят, что эксперимент удовлетворяет классическому определению вероятности, если пространство элементарных исходов состоит из конечного числа равновозможных исходов. В этом случае вероятность любого события вычисляется по формуле

называемой классическим определением вероятности, где символом обозначено число элементов конечного множества .

-----------------------------------------------------------------------------------------------------------------

Общее количество различных наборов при выборе  элементов из без возвращения и без учёта порядка равняется

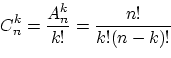
и называется числом сочетаний из элементов по элементов.

-------------------------------------------------------------------------------------------------------------------

Общее количество различных наборов при выборе элементов из без возвращения и с учётом порядка равняется

-------------------------------------------------------------------------------------------------------------

Общее количество различных наборов при выборе элементов из с возвращением и с учётом порядка равняется  .