Циклы газотурбинных установок (гту)

Газотурбинной установкой принято называть такой двигатель, где в качестве рабочего тела используется неконденсирующийся газ (воздух, продукты сгорания топлива), а в качестве тягового двигателя применяется газовая турбина. В отличие от поршневых ДВС, где процессы сжатия, подвода теплоты и расширения осуществляются в одном и том же цилиндре, в газотурбинных установках эти процессы происходят в различных элементах установки, в которые последовательно попадает поток рабочего тела.

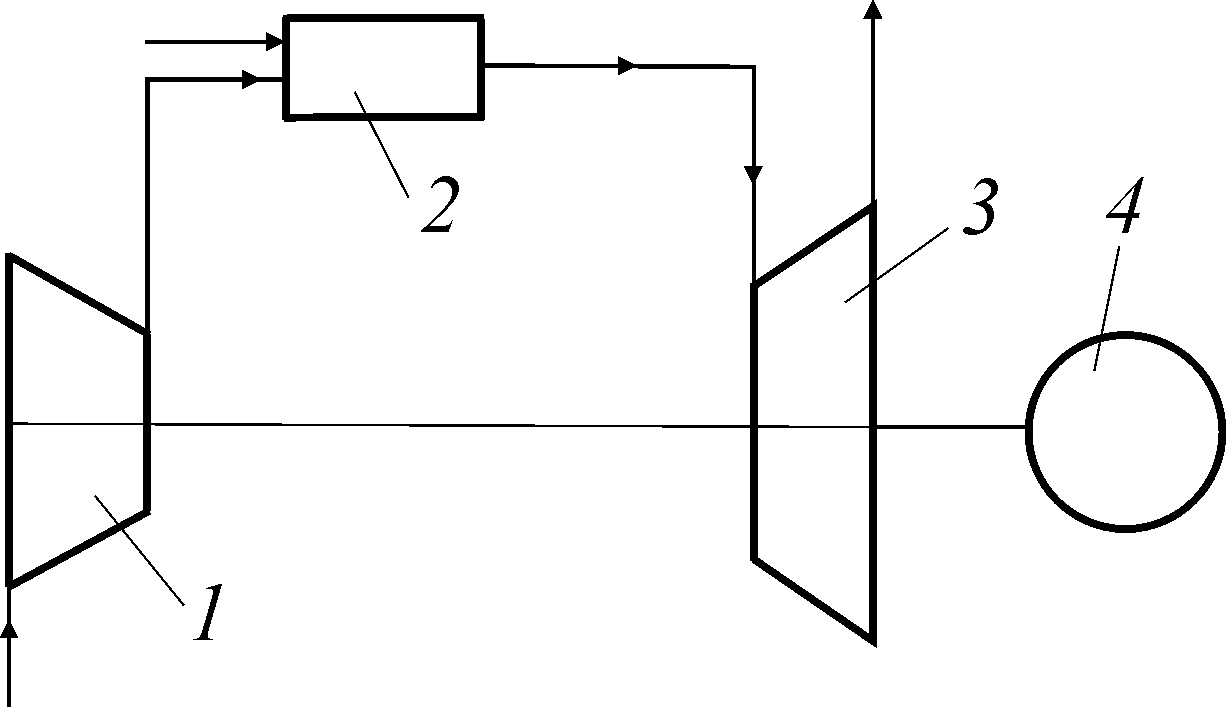
Рис. 48. Принципиальная схема газотурбинной установки

Газотурбинная установка простейшей схемы работает следующим образом: наружный воздух поступает на вход компрессора (1), где сжимается по адиабате (1–2) до давления р₂ (рис. 48, 49). После сжатия в компрессоре воздух поступает в камеру сгорания (2), куда одновременно подается жидкое или газообразное топливо и происходит процесс сгорания при (2–3). Образующиеся при сжигании топлива продукты сгорания поступают в газовую турбину (3), где расширяются по адиабате (3–4) практически до атмосферного давления р₁. Отработавшие продукты сгорания выбрасываются в атмосферу (4–1). а б

Рис. 49. Цикл газотурбинной установки с подводом теплоты при постоянном давлении в координатах p-v (а) и T-s (б)

В газотурбинных установках подвод теплоты к рабочему телу может осуществляться при постоянном давлении (цикл Брайтона) или при постоянном объеме (цикл Гемфри). Коэффициент полезного действия термодинамического цикла ГТУ с подводом теплоты при постоянном давлении (цикл Брайтона) определяется соотношением

(1)

Для газотурбинных установок вводят параметр, характеризующий степень повышения давления рабочего тела в компрессоре С = р₂/р₁. Выразим отношение температур в выражении (1) через соотношение давлений сжатия для компрессора С, используя уравнения адиабаты для идеального газа, в виде следующей системы уравнений:

; . (2)

Поскольку р₃ = р₂, а р₄ = р₁, то T₄/T₁ =T₃/T₂. С учетом этого равенства и системы уравнений (2), выражение для определения термического КПД цикла Брайтона примет вид

. (3)

Из соотношения (3) следует, что КПД цикла Брайтона повышается с увеличением значения степени повышения давления рабочего тела в компрессоре С.

Г ТУ, работающие по циклу Гемфри (1-2-3-4). . ГТУ такого типа имеют больший коэффициент полезного действия, чем ГТУ, работающие по циклу Брайтона.

Вопрос № 30

Циклы поршневых двигателей внутреннего сгорания

Поршневыми двигателями внутреннего сгорания (ДВС) называются двигатели, в которых топливо сжигается в цилиндрах, где возвратно-поступательно двигается поршень.

Несмотря на то, что цикл Карно имеет наивысший КПД, в реальных машинах он не реализуется. Дело в том, что цикл Карно, будучи сильно растянутым в координатах р–v, связан с весьма большими значениями удельного объема и давления.

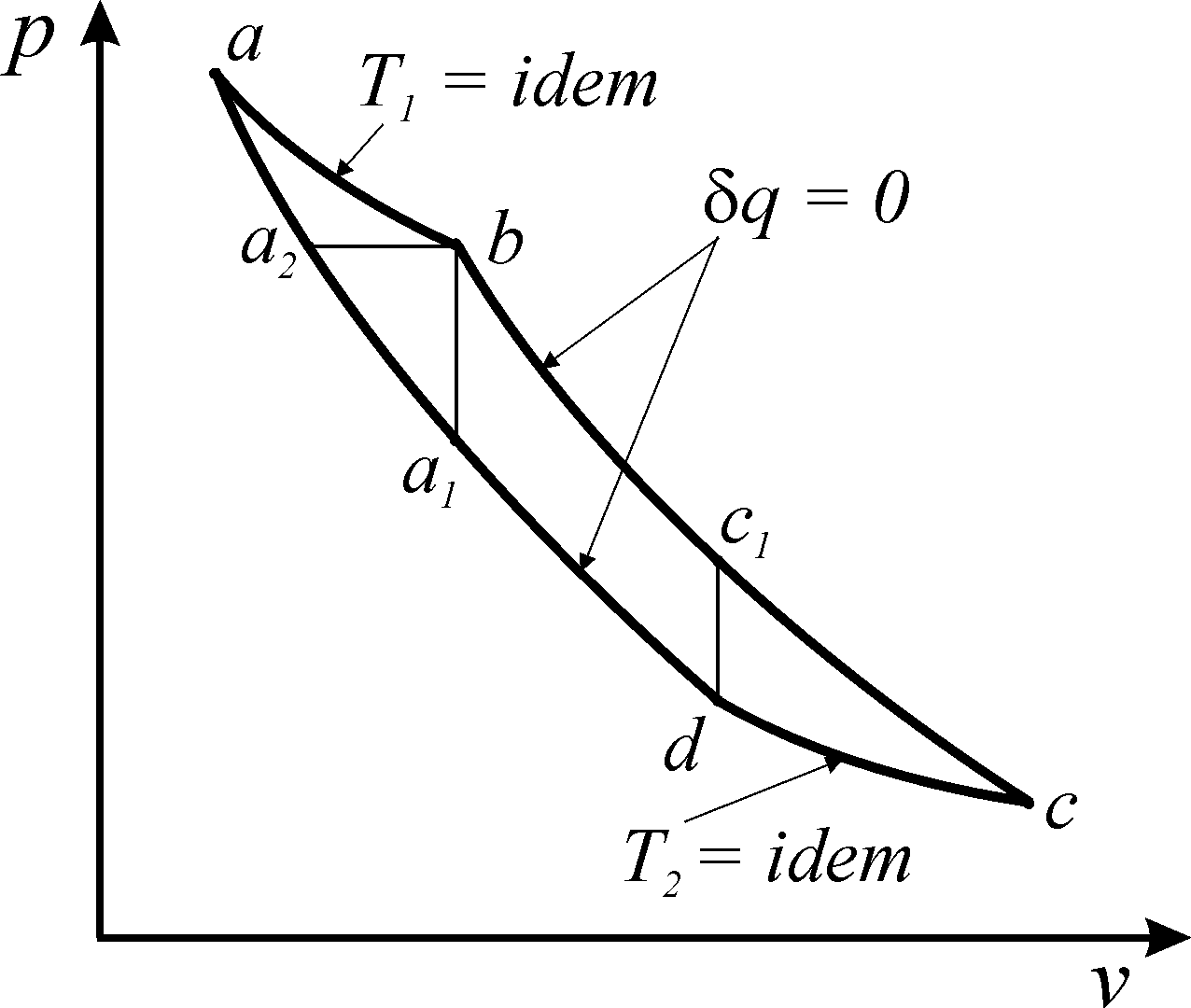
Рис. 43. Цикл Карно в координатах p-v

Отношение объема цилиндра к объему камеры сгорания = v_c/v_a (эта величина в поршневых ДВС называется степенью сжатия), работающего по циклу Карно, достигает 400, а давление в точке (а) – = 280 – 300 МПа.

Термодинамических циклы ДВС: цикл с подводом теплоты при постоянном объеме (цикл Отто),состоящий из двух изохор и двух адиабат (a₁-b-c₁-d-a₁) и цикл с подводом теплоты при постоянном давлении (цикл Дизеля), состоящий из изобары a₂–b, изохоры с₁–d и двух адиабат b–c₁ и d–a₂ (a₂-b-c₁-d- a₂). Полученные циклы имеют КПД меньше, чем КПД цикла Карно

Рис. 45. Цикл Отто в координатах p-v (а) и T-s (б)

Процесс (1–2) в цикле Отто характеризует адиабатное сжатие рабочего тела, процесс (2–3) - изохорный подвод теплоты q₁, процесс (3–4) - адиабатное расширение и процесс (4–1) - изохорный отвод теплоты q₂.

Полезная работа в цикле равна разности подведенной и отведенной теплоты и численно равна площади (1-2-3-4-1). Степень сжатия цикла весьма сильно влияет на КПД цикла. Чем выше степень сжатия, тем выше КПД цикла. Термический КПД цикла

.

Это значит, что КПД цикла Отто растет с увеличением степени сжатия.

Цикл Дизеля состоит из процесса адиабатного сжатия (1–2), изобарного подвода теплоты (2–3), адиабатного расширения (3–4) и изохорного отвода теплоты (4–1) (рис. 46). Степень сжатия в двигателях, работающих по циклу Дизеля, составляет = 14 – 18.

а б

Рис. 46. Циклы Отто и Дизеля в координатах p-v (а) и T-s (б)

Сравним между собой циклы Отто и Дизеля при одинаковых параметрах точек (1) и (4) с помощью диаграммы Т–s (рис. 46). Если в этих циклах будет одинаковая степень сжатия ε и одинаковое количество отводимой теплоты q₂ , то КПД цикла Отто будет выше КПД цикла Дизеля.

КПД цикла Дизеля, в условиях одинакового максимально возможного давления, больше, чем КПД цикла Отто.

Подачу топлива можно осуществлять так, что одна его часть будет сгорать при постоянном объеме, а другая – при постоянном давлении. Такой цикл называется циклом смешанного сгорания топлива или циклом Тринклера .Цикл со смешенным подводом теплоты занимает по эффективности промежуточное положение между циклами Отто и Дизеля как в условиях сравнения при одинаковой степени сжатия ε, так и при сравнении по условию одинакового максимального давления в цилиндре двигателя.

а б

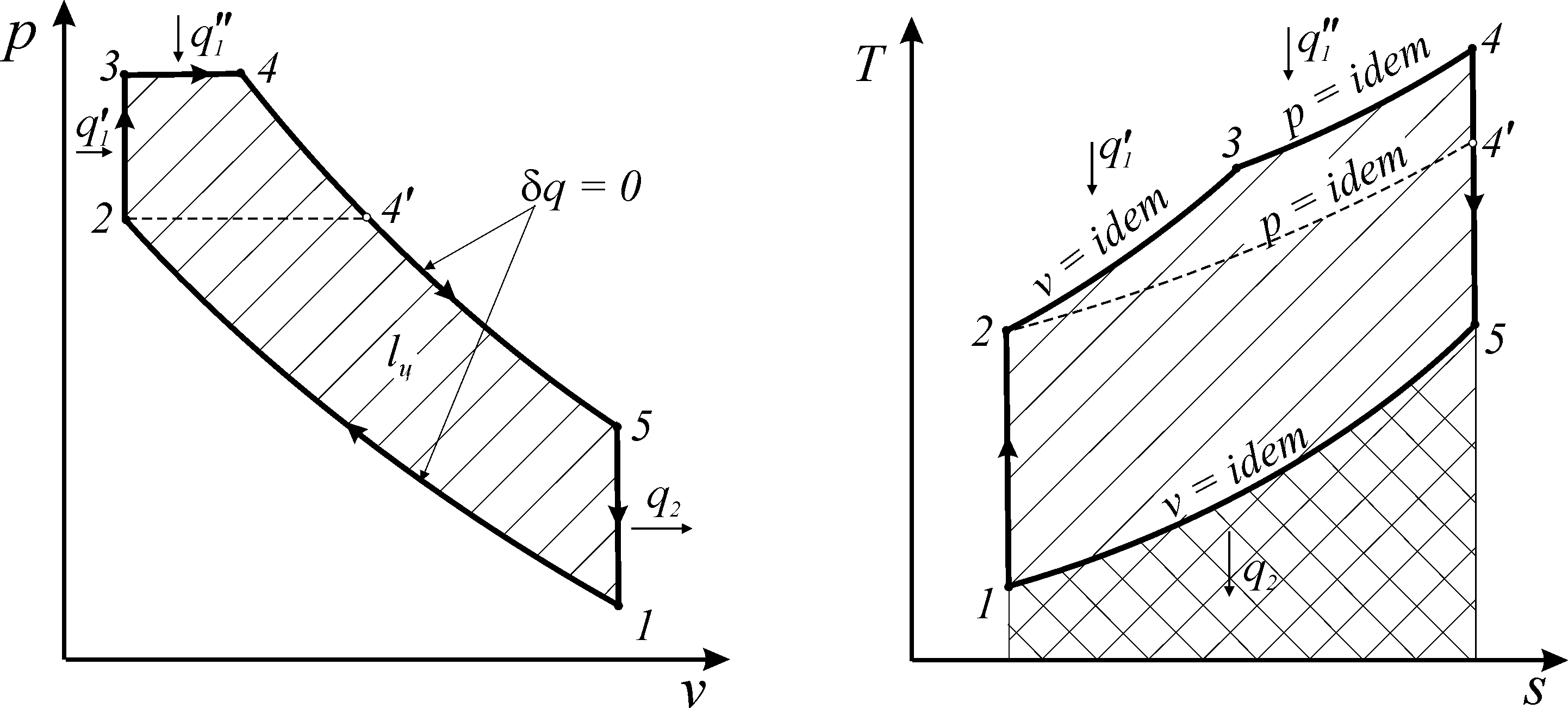
Рис. 47. Цикл смешанного сгорания в координатах p-v (а) и T-s (б)

Выведем уравнение для определения термического КПД смешанного цикла. Количество подводимой теплоты на изохоре (2–3) равно , а в изобарном процессе (3–4) – . Количество отводимой теплоты q₂ на изохоре (5–1) по абсолютной величине составляет . Следовательно, термический КПД цикла

.

Из уравнения видно, что КПД цикла со смешанным подводом теплоты растет с увеличением ε и λ и с уменьшением ρ. Если ρ = 1, то цикл со смешанным подводом теплоты превращается в цикл Отто, термический КПД которого находится из соотношения

Если λ = 1, то смешанный цикл превращается в цикл Дизеля, термический КПД которого находится из выражения

.

Вопрос №31