1. Понятие алгоритма. Свойства алгоритма. Способы записи алгоритмов. Блок-схема как графический способ записи алгоритма. Основные элементы блок-схемы.

Алгоритм - определённая последовательность

действий, которые необходимо выполнить, чтобы

получить результат. Алгоритм может представлять

собой некоторую последовательность вычислений,

а может - последовательность действий

нематематического характера. Для любого

алгоритма справедливы общие закономерности -

свойства алгоритма.

Свойства алгоритма:

- Дискретность.

- Понятность

- Детерминированность

- Массовость

- Результативность

ОПРЕДЕЛЁННОСТЬ НА КАЖДОМ ШАГЕ - каждое действие м. б .выполнено

наличие ВХоД И ВЫХОД ДАННЫЕ

Дискретность - свойство алгоритма, когда алгоритм

разбивается на конечное число элементарных

действий (шагов).

Понятность - свойство алгоритма, при котором

каждое из этих элементарных действий (шагов)

являются законченными и понятными.

Детерминированность - свойство, когда каждое

действие (операция.указание.шаг.требование)

должно

пониматься в строго определённом смысле, чтобы не

оставалась места произвольному толкованию. чтобы

каждый, прочитавший указание, понимал его

однозначно.

Массовость - свойство, когда по данному алгоритму

должна решаться не одна, а целый класс подобных

задач.

Результативность – свойство, при котором любой

алгоритм в процессе выполнения должен приводить к

определённому результату. Отрицательный результат

также является результатом.

Способы задания алгоритма:

- Словесный, (недостаток–многословность,

возможна неоднозначность)

- Табличный (физика, химия и т. д.)

- Графический (блок-схемы)

Графическая форма представления алгоритма

называется блок-схемой

Основные блоки алгоритмов:

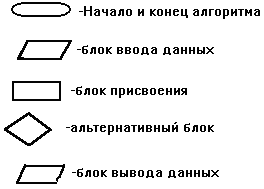
Все имеющиеся алгоритмы можно разделить

на 3 вида:

- Линейные алгоритмы

- Алгоритмы ветвления

- Циклические алгоритмы

Блок-схемой называют графическое

представление алгоритма, в котором он изображается

в виде последовательности связанных между собой

функциональных блоков, каждый из которых

соответствует выполнению одного или нескольких

действий. В блок-схеме каждому типу действий

(вводу исходных данных, вычислению значений

выражений, проверке условий, управлению

повторением действий, окончанию обработки и т.п.)

соответствует геометрическая фигура, представленная

в виде блочного символа. Блочные символы

соединяются линиями переходов, определяющими

очередность выполнения действий.

Приведем наиболее часто употребляемые символы.

Блок "процесс"

Применяется для обозначения действия или

последовательности действий, изменяющих значение,

форму представления или размещения данных.

Для улучшения наглядности схемы несколько

отдельных блоков обработки можно объединять в

один блок. Представление отдельных операций

достаточно свободно.

Блок "решение"

Используется для обозначения переходов управления

по условию. В каждом блоке "решение" должны быть

указаны вопрос, условие или сравнение,

которые он определяет.

Блок "модификация"

Используется для организации циклических

конструкций. (Слово модификация означает

видоизменение, преобразование). Внутри блока

записывается параметр цикла, для которого

указываются его начальное значение, граничное

условие и шаг изменения значения параметра

для каждого повторения.

Блок "предопределенный процесс"

Используется для указания обращений к

вспомогательным алгоритмам, существующим

автономно в виде некоторых самостоятельных

модулей, и для обращений к библиотечным

подпрограммам.

Блок "ввод-вывод"

Ввод-вывод в общем виде.

Блок "пуск-остановка "

Начало, конец алгоритма, вход и выход

в подпрограмму.

Блок "документ"

Начало, конец алгоритма, вход и выход

в подпрограмму.

2.Представление целого числа в различных системах исчисления. Десятичная, двоичная, восьмеричная и шестнадцатеричная системы исчисления. Хранение чисел в памяти компьютера. Прямой, обратный и дополнительный коды.

Совокупность приемов наименования и

обозначение чисел называется системой исчисления.

В качестве условных знаков для записи чисел

используются цифры. Система исчисления, в которой

значение каждой цифры в произвольном месте

последовательности цифр, обозначающей

запись числа, не изменяется, называется

непозиционной. Система исчисления, в которой

значение каждой цифры зависит от места в

последовательности цифр в записи числа,

называется позиционной.

Общепринятой в современном мире является

десятичная позиционная система исчисления,

которая из Индии через арабские страны пришла

в Европу. Основой системы является число десять.

Основой системы исчисления называется число,

означающее, во сколько раз единица следующего

разряда больше чем единица предыдущего.

Общеупотребительной формой записи числа является

сокращенная форма записи разложения по степеням

основы системы исчисления, например

130678=1*10⁵+3*10⁴+0*10³+6*10²+7*10¹+8

Здесь 10 служит основой системы исчисления,

а показатель степени - это номер позиции цифры

в записи числа (нумерация ведется слева на право,

начиная с нуля). Арифметические операции в этой

системе выполняют по правилам, предложенным еще

в средневековье. Например, складывая два

многозначных числа, применяем правило сложения

столбиком. При этом все сводится к сложению

однозначных чисел, для которых необходимо знать

таблицу сложения.

Проблема выбора системы исчисления для

представления чисел в памяти компьютера имеет

большое практическое значение. В случае ее выбора

обычно учитываются такие требования, как

надежность представления чисел при использовании

физических элементов, экономичность

(использование таких систем исчисления, в которых

количество элементов для представления чисел из

некоторого диапазона было бы минимальном).

Для изображения целых чисел от 1 до 999 в

десятичной системе достаточно трех разрядов, то есть

трех элементов. Поскольку каждый элемент может

находиться в десяти состояниях, то общее количество

состояний - 30, в двоичной системе исчисления:

99910=11111002, необходимое количество состояний -

20 (индекс внизу числа - основа системы исчисления).

Более распространенной для представления чисел в

памяти компьютера является двоичная система

исчисления. Для изображения чисел в этой системе

необходимо две цифры: 0 и 1, то есть достаточно двух

стойких состояний физических элементов. Эта система

близка к оптимальной по экономичности, и кроме того,

таблицы сложения и умножения в этой

системе элементарные

+	0		1
0	0		1
1	1		10
*		0		1
0		0		0
1		0		1

Поскольку 2³=8, а 2⁴=16 , то каждых три двоичных

разряда числа образовывают один восьмеричный,

а каждых четыре двоичных разряда - один

шестнадцатеричный. Поэтому для сокращения

записи адресов и содержимого оперативной памяти

компьютера используют шестнадцатеричную и

восьмеричную системы исчисления.

Для отладки программ и в других ситуациях в

программировании актуальной является проблема

перевода чисел из одной позиционной системы

исчисления в другую. Если основа новой системы

исчисления равняется некоторой степени старой

системы исчисления, то алгоритм перевода очень

простой: нужно сгруппировать справа налево разряды

в количестве, равном показателю степени и заменить

эту группу разрядов соответствующим символом

новой системы исчисления. Этим алгоритмом удобно

пользоваться при переводе числа из двоичной системы

исчисления в восьмиричную или шестнадцатеричную.

Например, 101102=10 110=26₈, 1011100₂=101 1100=5C₈

Перевод чисел из восьмеричной или

шестнадцатеричной систем исчисления в двоичную

происходит по обратному правилу: один символ

старой системы исчисления заменяется группой

разрядов новой системы исчисления, в количестве

равном показателю степени новой системы

исчисления. Например, 4728=100 111 010 =

100111010₂, B516=1011 0101=10110101₂

числа в доп-ом и обратном хранятся в виде дополнения,разница в коэффициентах в обр 10 в н-1 а в дополнительном

10. н

3.Основные принципы ООП. Инкапсуляция.

. Объектно-ориентированное программирование

или ООП (object-oriented programming) -

методология программирования, основанная на

представлении программы в виде совокупности

объектов, каждый из который является реализацией

определенного типа, использующая механизм

пересылки сообщений и классы, организованные в

иерархию наследования.

ООП характеризуется следующими принципами:

- Все является объектом

- Вычисления осуществляются путем взаимодействия

(обмена данными) между объектами, при котором

один объект требует, чтобы другой объект выполнил

некоторое действие; объекты взаимодействуют,

посылая и получая сообщения; сообщение - запрос на

выполнение действия, дополненный набором

аргументов, которые могут понадобиться при

выполнении действия;

- Каждый объект имеет независимую память, которая

состоит из других объектов;

- Каждый объект является представителем класса,

который выражает общие свойства объектов

данного типа;

- В классе задается функциональность

(поведение объекта); тем самым все объекты, которые

являются экземплярами одного класса, могут

выполнять одни и те же действия;

- Классы организованы в единую древовидную

структуру с общим корнем, называемую иерархией

наследования; память и поведение, связанное с

экземплярами определенного класса, автоматически

доступны любому классу, расположенному ниже в

иерархическом дереве.

Для поддержки принципов

объектно-ориентированного программирования

все ООП-языки, включая C#, имеют 3 характерных

черты: инкапсуляцию, полиморфизм и

наследование.

Инкапсуляция (encapsulation) - техника, при которой

несущественная с точки зрения интерфейса объекта

информация прячется внутри него.