
- •2.Скорость и ускорение точки при векторном и координатном способах задания движения.
- •Вектор скорости
- •3.Скорость и ускорение точки при естественном способе задания движения.
- •4.Касательное и нормальное ускорения.
- •5.Равномерное и равнопеременное движения точки.
- •7.Теорема о проекциях скоростей двух точек плоской фигуры. Мгновенный центр скоростей. Теорема о проекциях скоростей
Кинематика.
1.Способы задания движения точки. Траектория движения. Движение тела или материальной точки считают известным, если существует возможность определить их положение относительно выбранной системы отсчета в любой момент времени. Задание движения точки может быть осуществлено естественным или координатным способами. Геометрическое место всех положений движущейся точки М называют её траекторией.
2.Скорость и ускорение точки при векторном и координатном способах задания движения.
Векторный способ
задания движения: Положение
точки М в пространстве определяется её
радиус–вектором
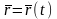 .
Траекторией является геометрическое
место концов вектора
.
Траекторией является геометрическое
место концов вектора

Вектор скорости
Скоростью точки М, определяющей как быстро и в каком направлении она движется в данный момент времени t, называют предел
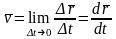
Вектор скорости равен первой производной от радиуса-вектора точки по времени.
Так как предельным
положением секущей ММ1
является касательная к траектории
точки, то и вектор ее скорости
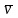 в данный момент времени t
направлен по касательной к траектории
в сторону движения.
Вектор ускорения
в данный момент времени t
направлен по касательной к траектории
в сторону движения.
Вектор ускорения
Величину
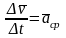 называют средним ускорением точки за
время
называют средним ускорением точки за
время
 .
Предел отношения
.
Предел отношения
 ,
,
характеризующий изменение скорости в данный момент времени t, называют ускорением точки.
Вектор ускорения равен первой производной от вектора скорости точки по времени или второй производной от радиуса-вектора точки по времени.
Ускорение
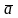 ,
направлено в сторону вогнутости
траектории.
,
направлено в сторону вогнутости
траектории.
Координатный
способ задания движения.
В прямолинейной
системе координат Oxyz
вектор
 может быть представлен в виде
может быть представлен в виде
 ,
,

координаты точки М, определяющие закон ее движения в зависимости от времени t ;
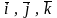 -
нормированный базис Oxyz.
-
нормированный базис Oxyz.
Согласно теореме о проекциях производной вектора.
1. Проекции скорости на оси координат равны первым производным от соответствующих координат точки по времени:
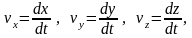
2. Проекции ускорения на оси координат равны первым производным от проекций скоростей точки или вторым производным от соответствующих координат точки по времени:
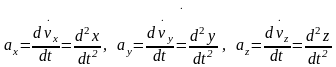
Величины (модули) скорости и ускорения в декартовой ортогональной системе координат определяют по формулам
 ,
,
а направления и характеризуют их направляющие косинусы
 .
.
3.Скорость и ускорение точки при естественном способе задания движения.
Предельное
положение прямой, проходящей через
точки М
и М1
траектории L
точки М, когда М1
стремится к М, определяет касательную
к этой кривой в точке М. Обозначим
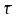 - единичный направляющий вектор
касательной к L
в точке М.
- единичный направляющий вектор
касательной к L
в точке М.
Соприкасающаяся плоскость в точке М кривой L определяется как предельное положение плоскости, содержащей в себе касательную в точке М кривой и любую точку М1 на ней, когда М1 стремится к М.
Нормаль
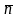 к кривой в точке М, лежащую в соприкасающейся
плоскости, называют главной
нормалью к
кривой в т.М. Нормаль
к кривой в точке М, лежащую в соприкасающейся
плоскости, называют главной
нормалью к
кривой в т.М. Нормаль
 к кривой, перпендикулярную соприкасающейся
плоскости, называют бинормалью.
к кривой, перпендикулярную соприкасающейся
плоскости, называют бинормалью.
Прямоугольную
систему взаимно ортогональных осей,
направленных по
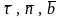 называют естественными
осями кривой L.
называют естественными
осями кривой L.
Направление вектора скорости принимают за положительное направление касательной . Положительное направление главной нормали считают в сторону вогнутости кривой, а бинормаль направляют так, чтобы получившаяся система осей являлась правой.
Кривизной «k» кривой L в точке М называют предел
 .
.
Радиусом кривизны «» кривой L в точке М называют величину обратную ее кривизне в этой точке
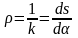 .
.
Так, например, дуга
окружности длиной s,
опирающаяся на центральный угол
 ,
,
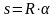 ,
где R
– радиус окружности, то радиус
кривизны для
окружности
,
где R
– радиус окружности, то радиус
кривизны для
окружности
 .
.
