
”Функціональні та степеневі ряди”
Функціональним рядом називають ряд вигляду...
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Степеневий ряд – це функціональний ряд вигляду...
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Функціональний ряд
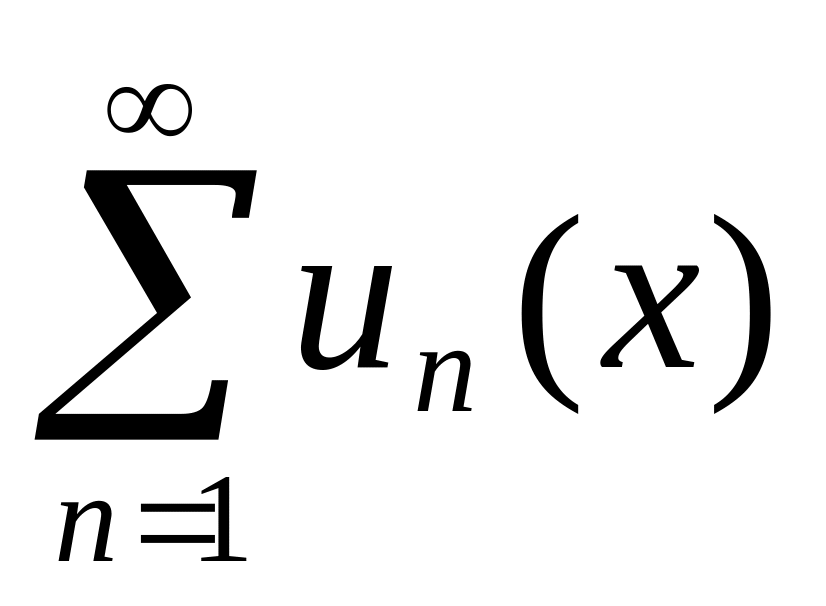 називається збіжним, якщо...
називається збіжним, якщо...
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Областю збіжності функціонального ряду називається...
а) множина всіх точок його
збіжності; б) множина
![]() ;
;
в) множина всіх точок його
розбіжності; г) множина
![]() .
.
Інтервалом збіжності степеневого ряду
 є...
є...
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Радіус збіжності степеневого ряду визначають за формулою...
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Радіус збіжності степеневого ряду визначають за формулою...
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Якщо
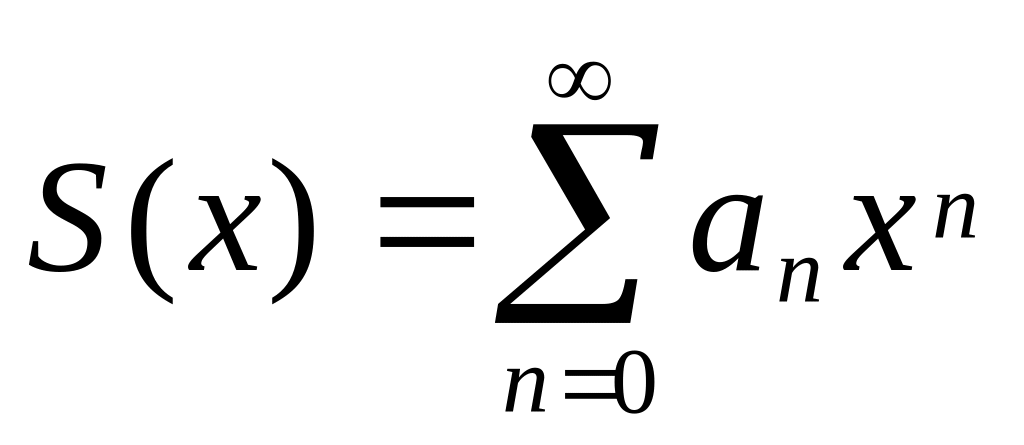 ,
то...
,
то...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Якщо , то...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Сума
 степеневого ряду
степеневого ряду
 є...
є...
а) неперервною функцією всередині інтервалу збіжності ряду;
б) неперервною функцією за межами інтервалу збіжності ряду;
в) обмеженою функцією всередині інтервалу збіжності ряду;
г) обмеженою функцією за межами інтервалу збіжності ряду.
Функціональний ряд є абсолютно і рівномірно збіжним на множені
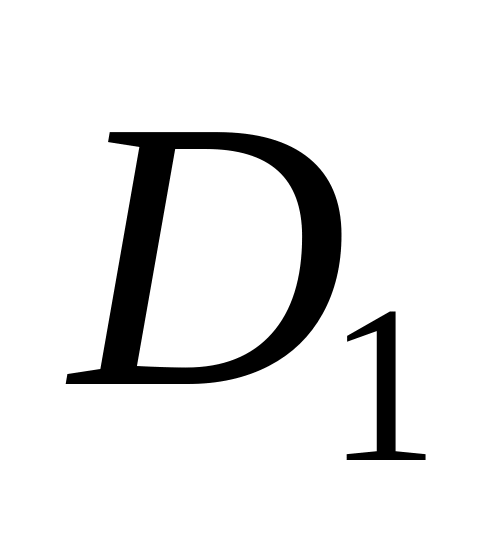 ,
якщо існує знакододатний збіжний
числовий ряд
такий, що для всіх
,
якщо існує знакододатний збіжний
числовий ряд
такий, що для всіх
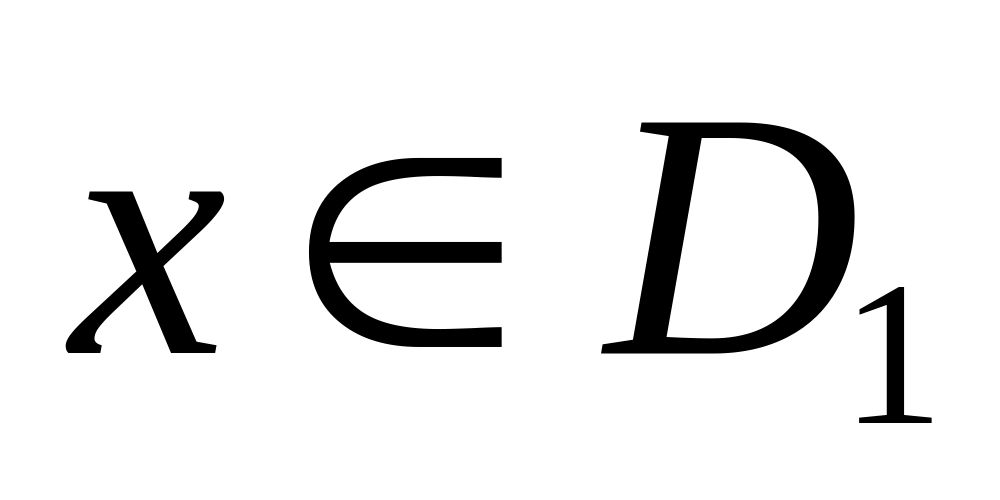 члени ряду задовольняють нерівності...
члени ряду задовольняють нерівності...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Функціональний ряд називається рівномірно збіжним до своєї суми на множені , якщо для довільного числа існує таке число
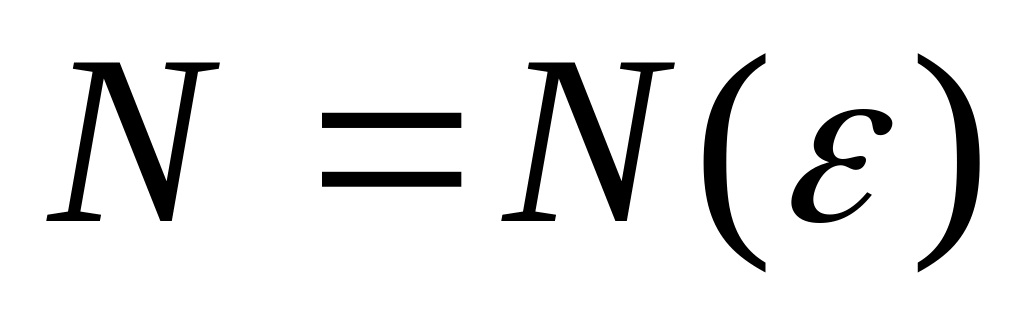 ,
яке залежить лише від
і не залежить від
,
що для всіх
,
яке залежить лише від
і не залежить від
,
що для всіх
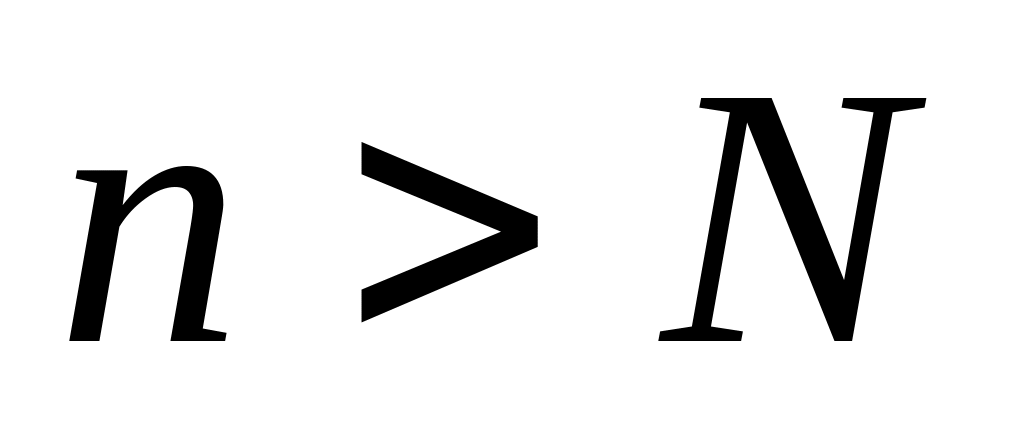 і для всіх
і для всіх
 виконується нерівність...
виконується нерівність...
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
”Обчислення границь функцій декількох змінних”
Функцією багатьох дійсних змінних називають...
а) закон, який кожній точці
![]() множини
множини
![]() ставить у відповідність єдине дійсне
число
ставить у відповідність єдине дійсне
число
![]() ;
;
б) закон, який кожній точці множини ставить у відповідність єдине ціле число ;
в) закон, який кожній точці множини ставить у відповідність єдине раціональне число ;
г) закон, який кожній точці множини ставить у відповідність єдине ірраціональне число .
Областю визначення функції
 називається...
називається...
а) сукупність усіх значень
аргументів
![]() ,
при яких функція
,
при яких функція
![]() набуває певних дійсних значень;
набуває певних дійсних значень;
б) сукупність усіх значень аргументів , при яких функція набуває певних цілих значень;
в) сукупність усіх значень аргументів , при яких функція набуває певних раціональних значень;
г) сукупність усіх значень аргументів , при яких функція набуває певних ірраціональних значень.
Рівняння лінії рівня функції
 має вигляд...
має вигляд...
а)
![]() ,
; б)
,
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
Поверхня рівня функції має вигляд...
а)
![]() ,
; б)
,
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Число називається границею функції
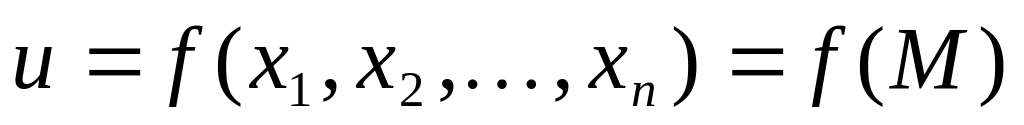 у точці
у точці
 ,
якщо...
,
якщо...
а) для будь – якого додатного
існує таке додатне
,
що для всіх точок
з
- околу точки
виконується нерівність
![]() ;
;
б) для будь – якого додатного
існує таке додатне
,
що для всіх точок
з
- околу точки
виконується нерівність
![]() ;
;
в) для будь – якого додатного
існує таке додатне
,
що для всіх точок
з
- околу точки
виконується нерівність
![]() ;
;
г) для будь – якого додатного
існує таке додатне
,
що для всіх точок
з
- околу точки
виконується нерівність
![]() .
.
Функція
 називається неперервною в точці
,
якщо...
називається неперервною в точці
,
якщо...
а) вона визначена в цій точці
та її околі і
![]() ;
;
б) вона визначена в цій точці
та її околі і
![]() ;
;
в) вона визначена в цій точці
та її околі і
![]() ;
;
г) вона визначена в цій точці
та її околі і
![]() .
.
Точки в яких порушається неперервність, називаються...
а) точками розриву цієї функції;
б) стаціонарними точками цієї функції;
в) критичними точками цієї функції;
г) точками перегину цієї функції.
Повним приростом функції у точці
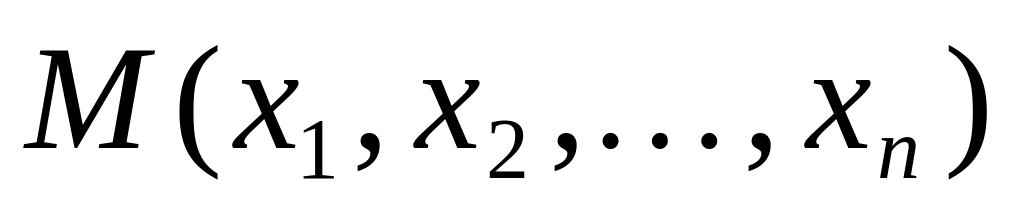 називається вираз вигляду...
називається вираз вигляду...
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Повний диференціал функції кількох змінних визначається за формулою...
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Повний диференціал функції двох змінних обчислюється за формулою...
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Рівняння дотичної площини до поверхні в точці
 має вигляд...
має вигляд...
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Якщо поверхня задана рівнянням
 і точка
належить поверхні, то рівняння дотичної
площини до поверхні в точці
має вигляд...
і точка
належить поверхні, то рівняння дотичної
площини до поверхні в точці
має вигляд...
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
”ОБЧИСЛЕННЯ ТА ЗАСТОСУВАННЯ КРАТНИХ ІНТЕГРАЛІВ”
При переході у подвійному інтегралі від прямокутних координат
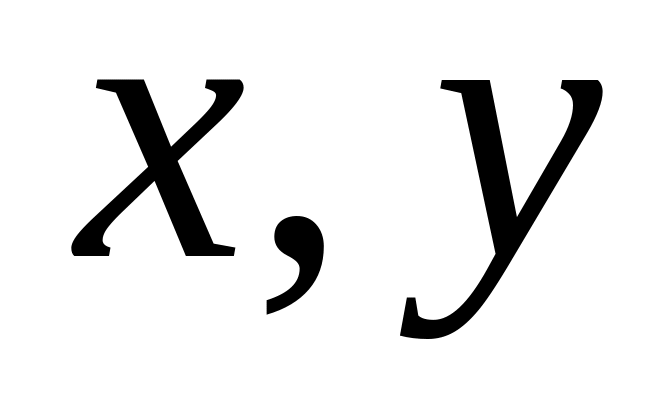 до полярних
до полярних
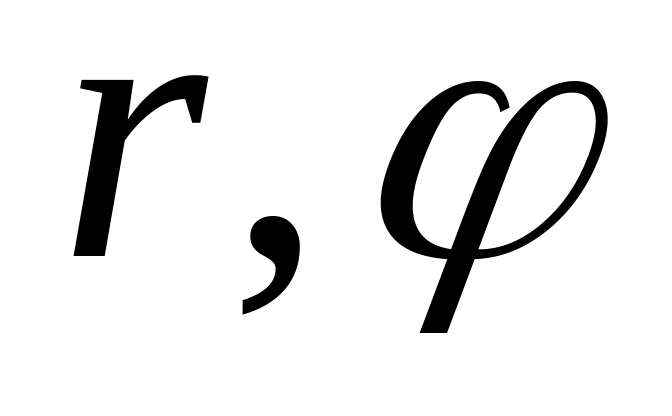 пов’язаних з прямокутними координатами
співвідношеннями
пов’язаних з прямокутними координатами
співвідношеннями
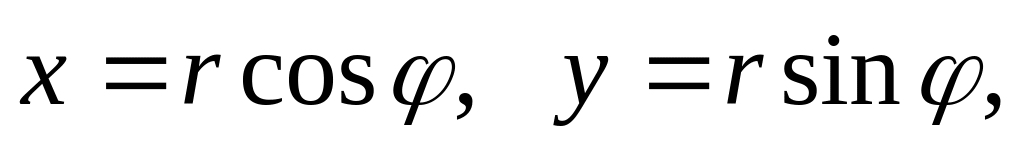 має місце формула...
має місце формула...
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
Якщо область інтегрування обмежена проміннями
 та
та
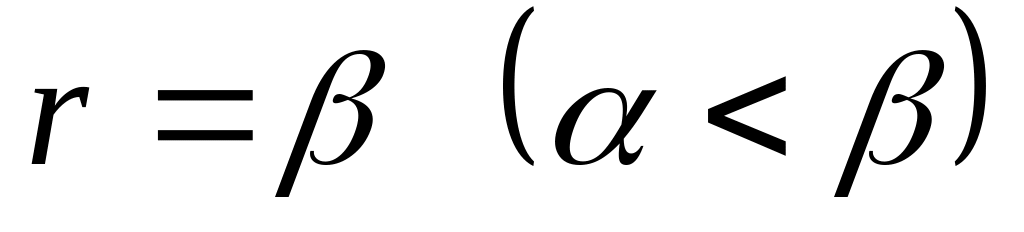 та кривими
та кривими
 та
та
 ,
де
,
де
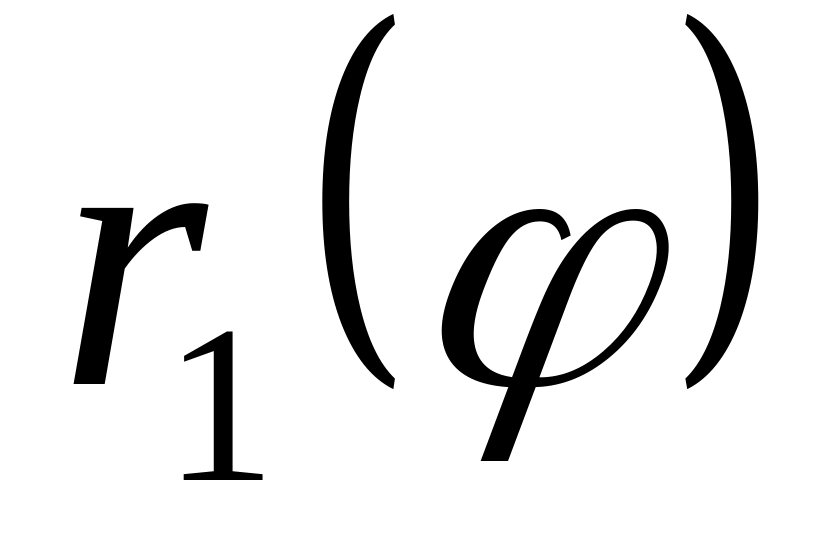 та
та
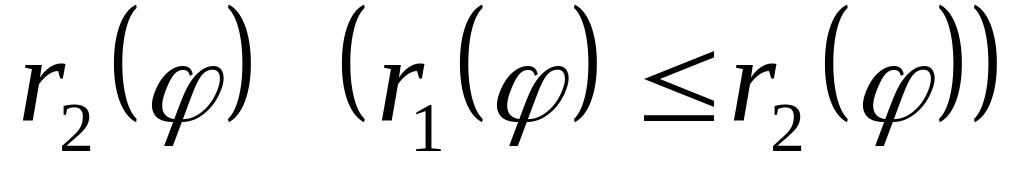 − однозначні функції на відрізку
− однозначні функції на відрізку
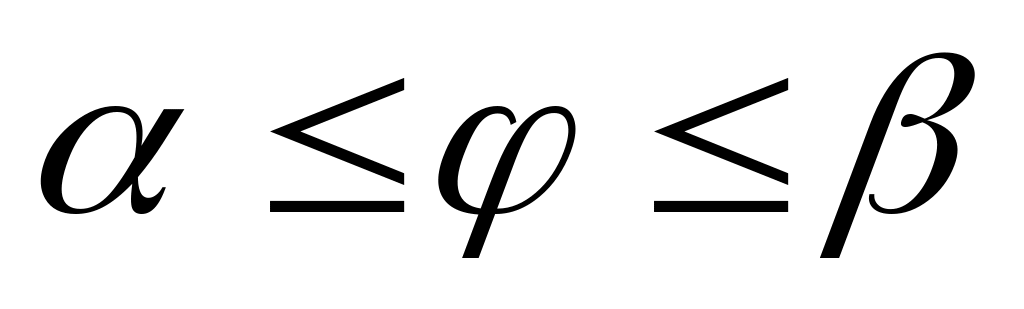 ,
то подвійний інтеграл може бути обчислені
за формулою...
,
то подвійний інтеграл може бути обчислені
за формулою...
а)
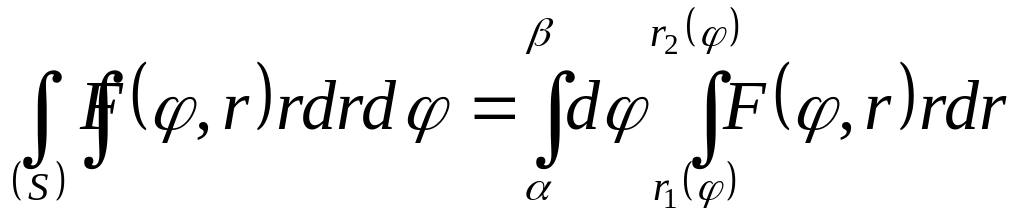 ;
б)
;
б)
 ;
;
в)
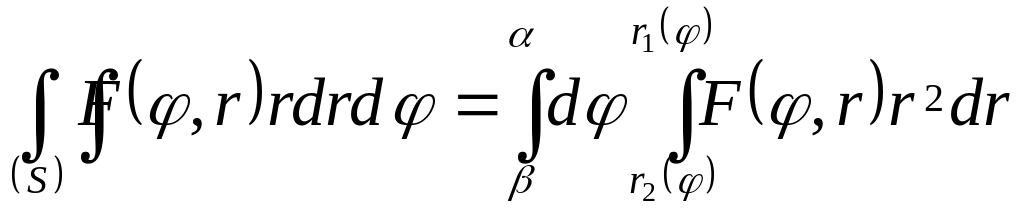 ; г)
; г)
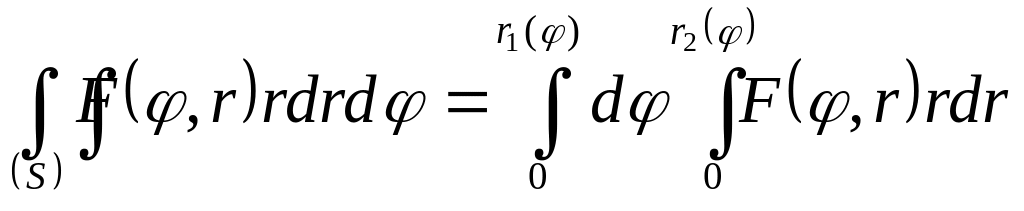 .
.
Якщо функція
 визначена в області
визначена в області
 то подвійний інтеграл обчислюється за
формулою...
то подвійний інтеграл обчислюється за
формулою...
а)
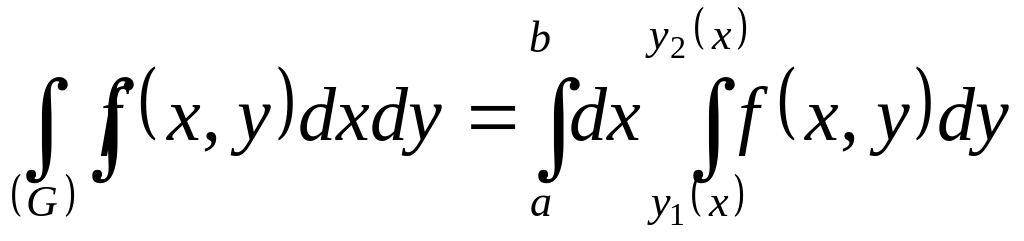 ; б)
; б)
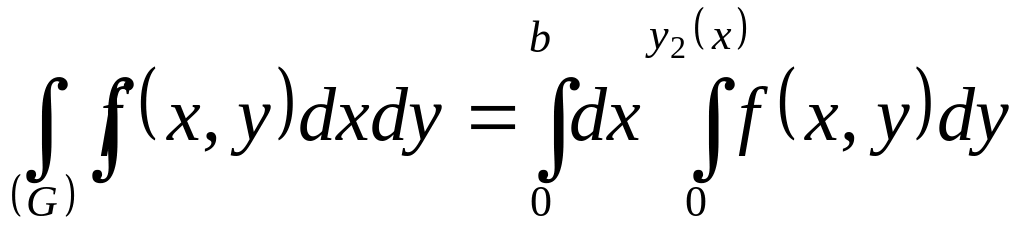 ;
;
в)
 ; г)
; г)

Якщо функція визначена в області
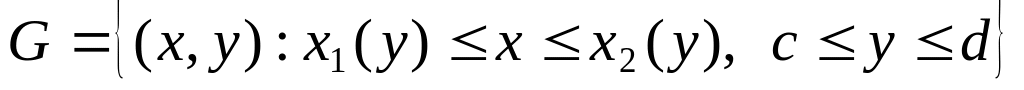 то подвійний інтеграл обчислюється за
формулою...
то подвійний інтеграл обчислюється за
формулою...
а)
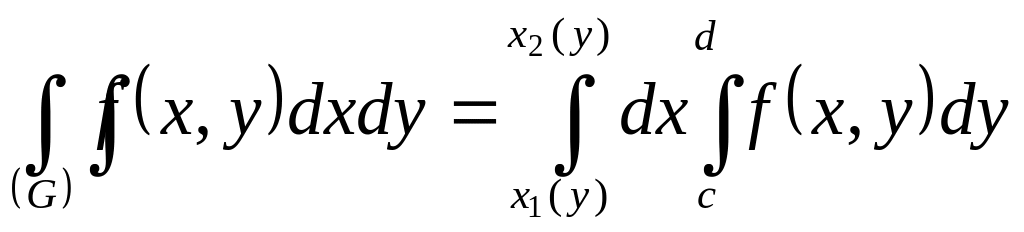 ; б)
; б)
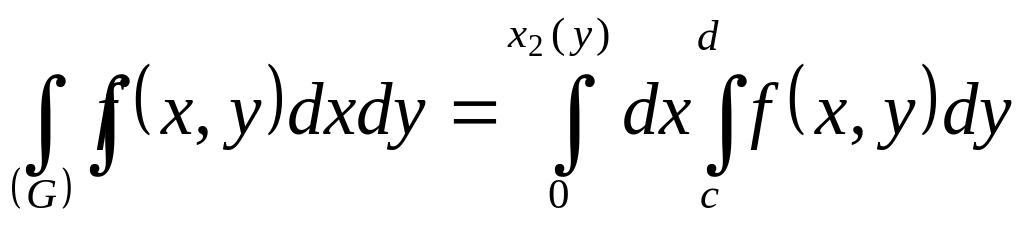 ;
;
в)
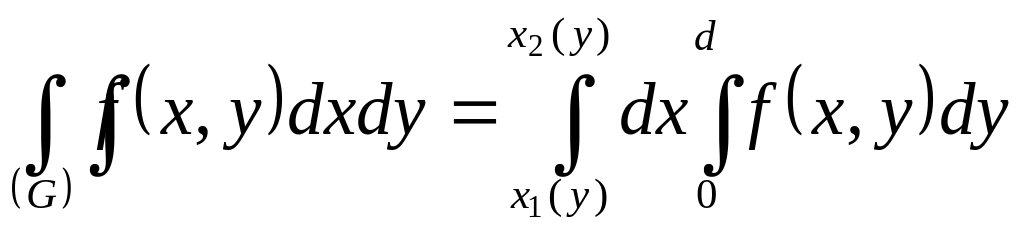 ; г)
; г)
 .
.
Площа квадрируємої області
 на площині
на площині
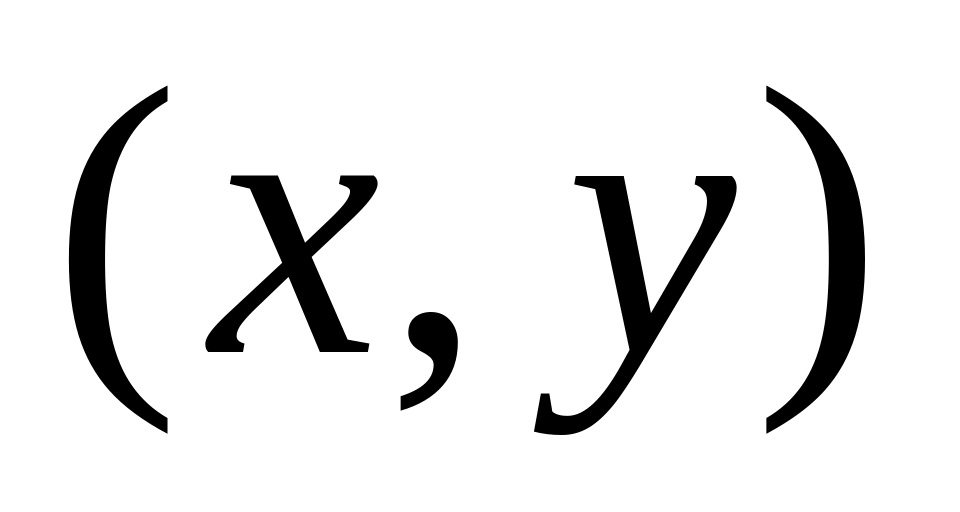 виражається формулою...
виражається формулою...
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
Об’єм
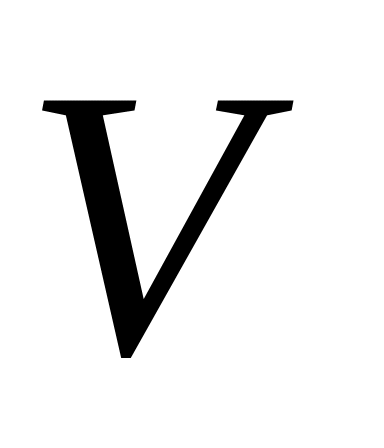 тіла
тіла
 ,
де
- квадрируєма замкнена область,
- неперервна невід’ємна в області
функція, обчислюється за формулою...
,
де
- квадрируєма замкнена область,
- неперервна невід’ємна в області
функція, обчислюється за формулою...
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Якщо - матеріальна нескінченно тонка пластина з густиною
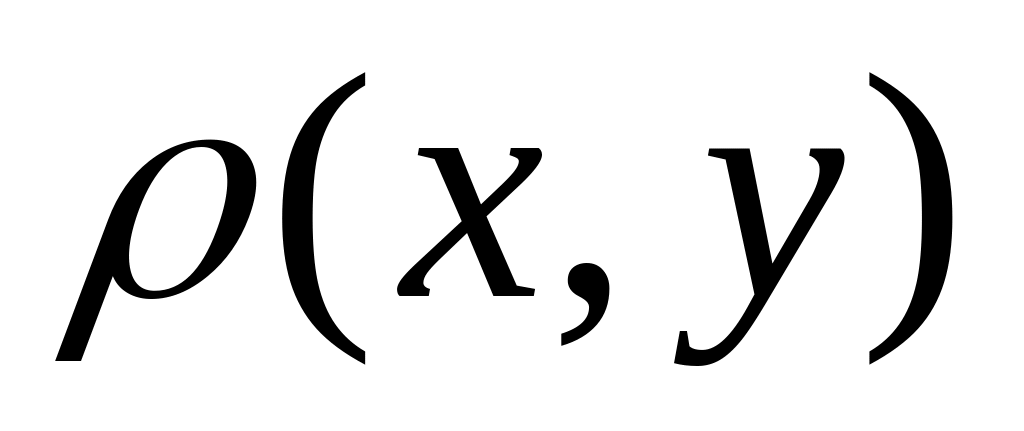 ,
то маса пластини обчислюється за
формулою...
,
то маса пластини обчислюється за
формулою...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Якщо - матеріальна нескінченно тонка пластина з густиною , то статичні моменти пластини відносно та
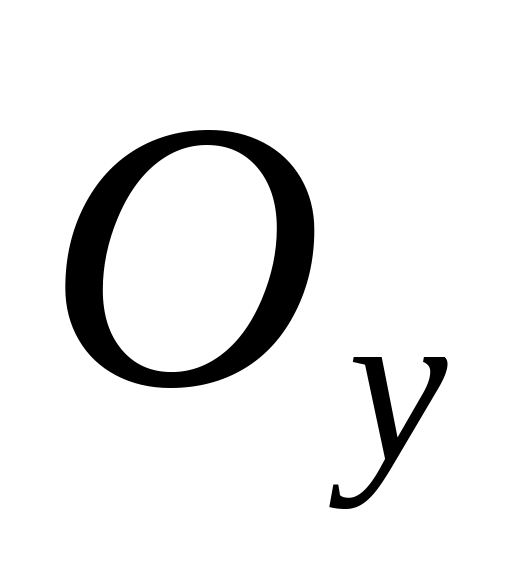 обчислюються за формулами...
обчислюються за формулами...
а)
![]() та
та
![]() ;
;
б)
![]() та
та
![]() ;
;
в)
![]() та
та
![]() ;
;
г)
![]() та
та
![]() .
.
Якщо - матеріальна нескінченно тонка пластина з густиною , то координати центру ваги пластини обчислюються за формулами...
а)
![]()
![]() ; б)
; б)
![]()
![]() ;
;
в)
![]()
![]() ; г)
; г)
![]()
![]() .
.
Якщо - матеріальна нескінченно тонка пластина з густиною , то моменти інерції пластини обчислюються за формулами...
а)
![]()
![]() ;
;
б)
![]()
![]() ;
;
в)
![]()
![]() ;
;
г)
![]()
![]() .
.
Якщо - матеріальна нескінченно тонка пластина з густиною , то момент інерції відносно початку координат обчислюється за формулою...
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
Якщо область визначена нерівностями
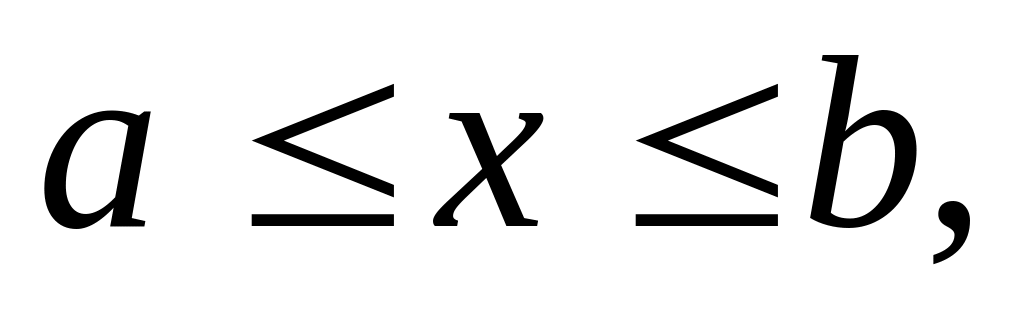
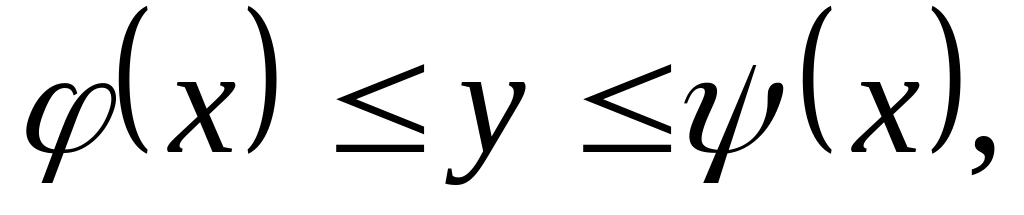 то площа обчислюється за формулою...
то площа обчислюється за формулою...
а)
 ; б)
; б)
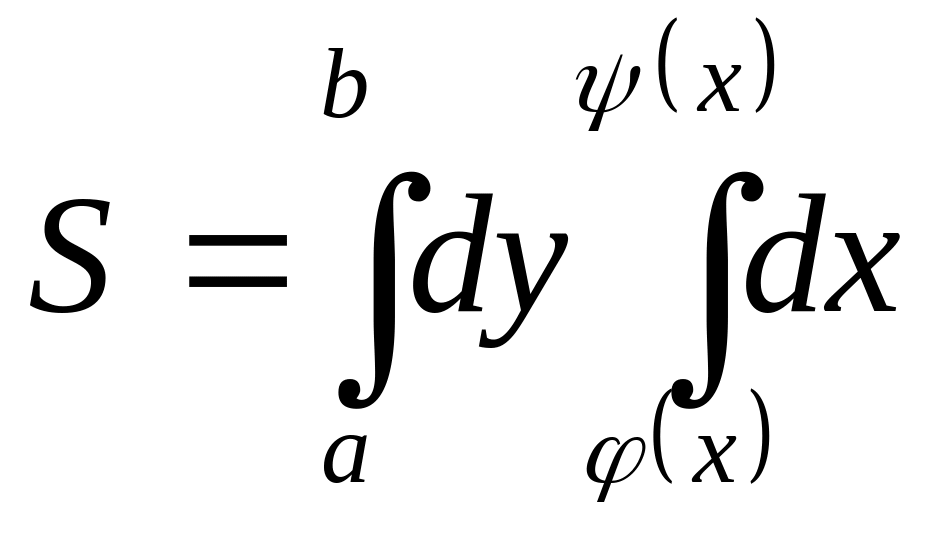 ; в)
; в)
![]() ; г)
; г)
 .
.
”Обчислення криволінійних інтегралів”
Якщо
 − неперервна функція,
− неперервна функція,
 − деяка гладка крива
,
− деяка гладка крива
,
 - диференціал дуги, то
криволінійний інтеграл першого роду
обчислюється за формулою...
- диференціал дуги, то
криволінійний інтеграл першого роду
обчислюється за формулою...
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
Якщо крива задана параметрично ,
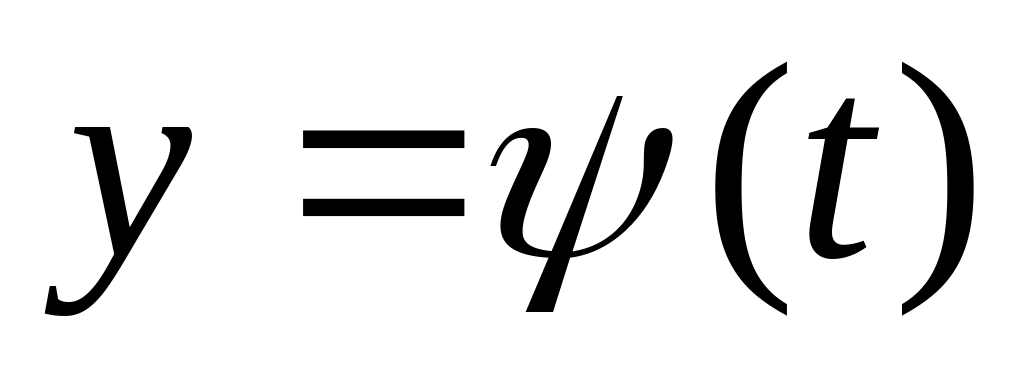
 ,
то криволінійний інтеграл першого роду
обчислюється за формулою...
,
то криволінійний інтеграл першого роду
обчислюється за формулою...
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Якщо
 та
та
 − неперервні функції,
− неперервні функції,
 − гладка крива
,
яка пробігає при змінені
від
до
,
то відповідний криволінійний інтеграл
другого роду виражається...
− гладка крива
,
яка пробігає при змінені
від
до
,
то відповідний криволінійний інтеграл
другого роду виражається...
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Якщо крива задана параметрично , , то відповідний криволінійний інтеграл другого роду виражається...
а) ;
б) ;
в) ;
г) .
Формула Гріна має вигляд...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Якщо при обчисленні криволінійного інтегралу ІІ роду контур інтегрування замкнений, то...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ,
,
![]() ; г)
; г)
![]() ,
.
,
.
Якщо − матеріальна плоска крива з лінійною густиною
 ,
то маса кривої обчислюється за формулою...
,
то маса кривої обчислюється за формулою...
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Якщо − матеріальна плоска крива з лінійною густиною , то статичні моменти кривої відносно та обчислюються за формулою...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Якщо − матеріальна плоска крива з лінійною густиною , то координати центру ваги кривої обчислюються за формулою...
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Якщо − матеріальна плоска крива з лінійною густиною , то момент інерції відносно початку координат обчислюється за формулою...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Якщо − матеріальна плоска крива з лінійною густиною , то моменти інерції відносно та обчислюються за формулою...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Робота сили
 при переміщенні матеріальної точки
маси 1 з точки
у точку
вздовж кривої
при переміщенні матеріальної точки
маси 1 з точки
у точку
вздовж кривої
 обчислюється за формулою
обчислюється за формулою
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
