
”Безпосереднє інтегрування”
Функцію
 називають первісною для функції
називають первісною для функції
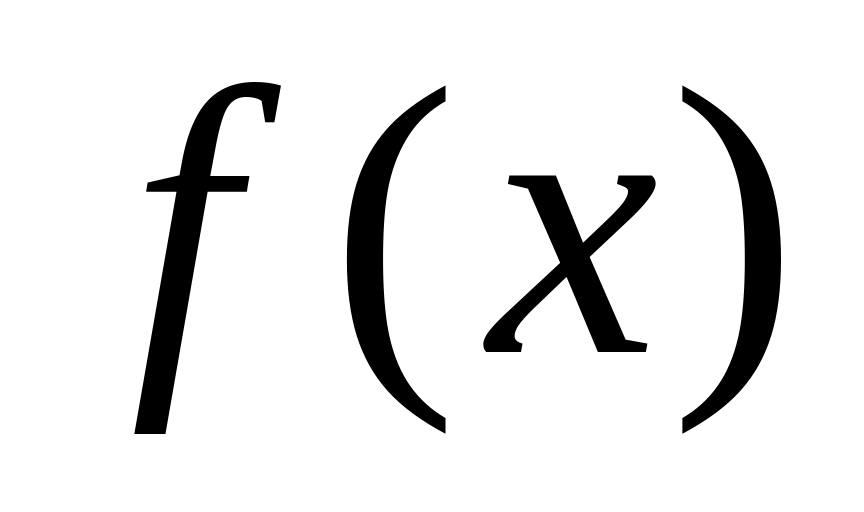 на проміжку
на проміжку
 ,
якщо в кожній точці
,
якщо в кожній точці
 виконується умова...
виконується умова...
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
Совокупність
 всіх первісних функції
на множені
називають...
всіх первісних функції
на множені
називають...
а) невизначеним інтегралом; б) похідною;
в) первісною; г) визначеним інтегралом.
У формулі

 називають...
називають...
а) підінтегральним виразом; б) підінтегральною функцією;
в) змінною інтегрування; г) сталою інтегрування.
У формулі називають...
а) підінтегральною функцією; б) підінтегральним виразом;
в) змінною інтегрування; г) сталою інтегрування.
У формулі
 називають...
називають...
а) змінною інтегрування; б) підінтегральним виразом;
в) підінтегральною функцією; г) сталою інтегрування.
У формулі
 називають...
називають...
а) сталою інтегрування; б) підінтегральним виразом;
в) підінтегральною функцією; г) змінною інтегрування.
Похідна від невизначеного інтеграла дорівнює...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Диференціал від невизначеного інтеграла дорівнює...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Невизначений інтеграл від суми двох функцій дорівнює...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Невизначений інтеграл від різниці двох функцій дорівнює...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Метод заміни змінної полягає у використанні формули...
а)
![]() ,
де
,
де
![]() ;
б)
;
б)
![]() ,
де
;
,
де
;
в)
![]() ,
де
;
г)
,
де
;
г)
![]() ,
де
.
,
де
.
Формула інтегрування по частинах має вигляд...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
”Обчислення визначених інтегралів та їх застосування”
Формула Ньютона – Лейбніца має вигляд...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Формула інтегрування по частинах у визначеному інтегралі має вигляд...
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Заміна змінної у визначеному інтегралі здійснюється за допомогою формули...
а)
![]() ,
де
,
де
![]() ,
,
![]() ,
,
![]() ;
;
б)
![]() ,
де
,
,
;
,
де
,
,
;
в)
![]() ,
де
,
,
;
,
де
,
,
;
г)
![]() ,
де
,
,
.
,
де
,
,
.
Площа криволінійної трапеції, обмеженої кривою (
 ),
прямими
і
),
прямими
і
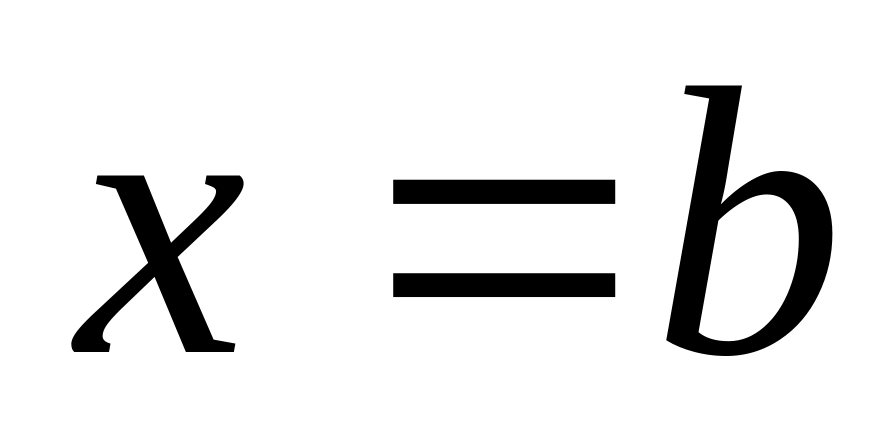 ,
відрізком
,
відрізком
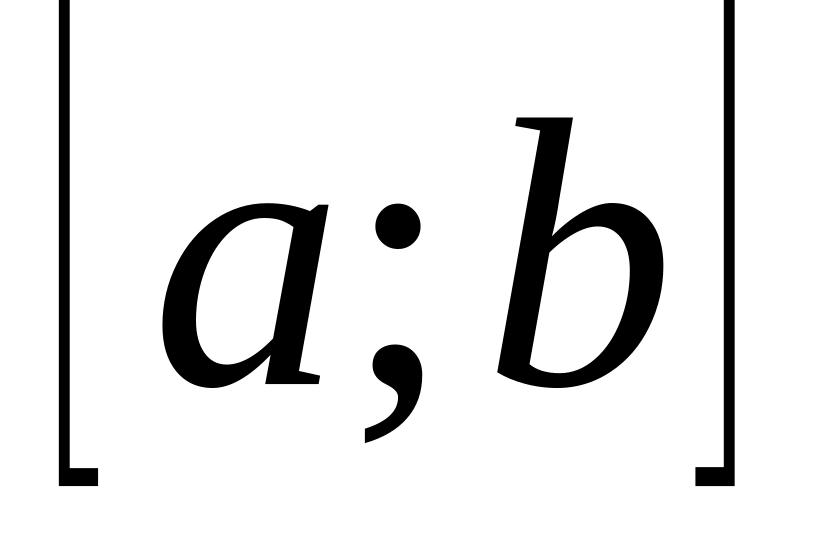 осі
,
обчислюється за формулою...
осі
,
обчислюється за формулою...
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
Якщо крива задана параметрично рівняннями
 ,
то площа криволінійної трапеції,
обмеженої цією кривою, прямими
і
,
відрізком
осі
,
обчислюється за формулою...
,
то площа криволінійної трапеції,
обмеженої цією кривою, прямими
і
,
відрізком
осі
,
обчислюється за формулою...
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Площа криволінійного сектора, обмеженого кривою, заданою в полярній системі координат рівнянням
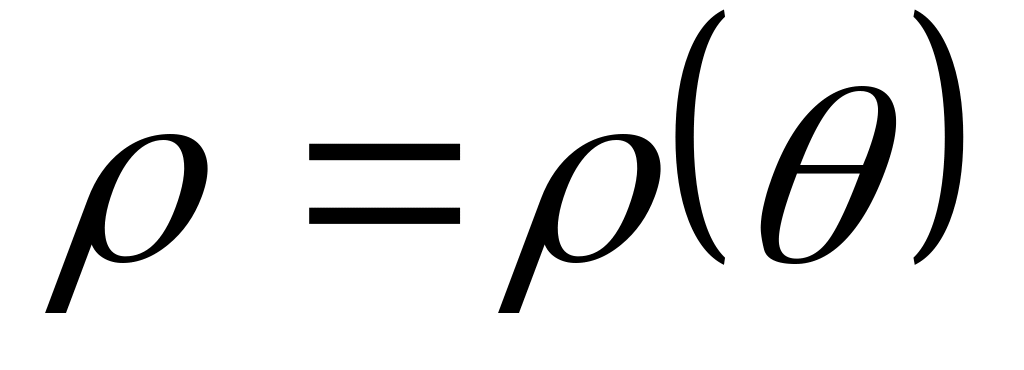 і двома полярними радіусами
і двома полярними радіусами
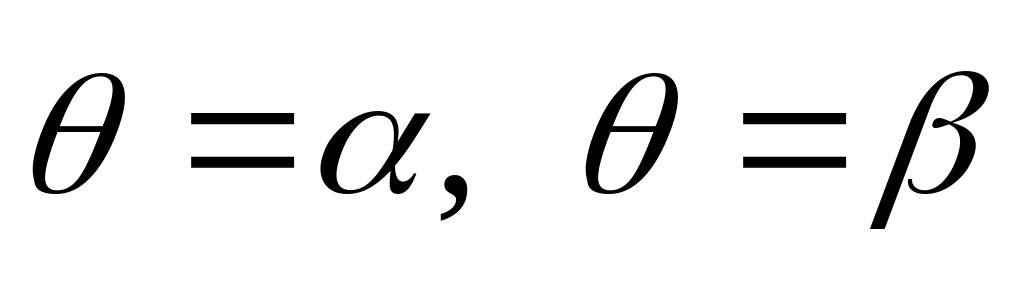 (
( ),
визначається за формулою...
),
визначається за формулою...
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Довжина дуги кривої на відрізку обчислюється за формулою...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Довжина дуги кривої, заданої параметрично (
 )
обчислюється за формулою...
)
обчислюється за формулою...
а)
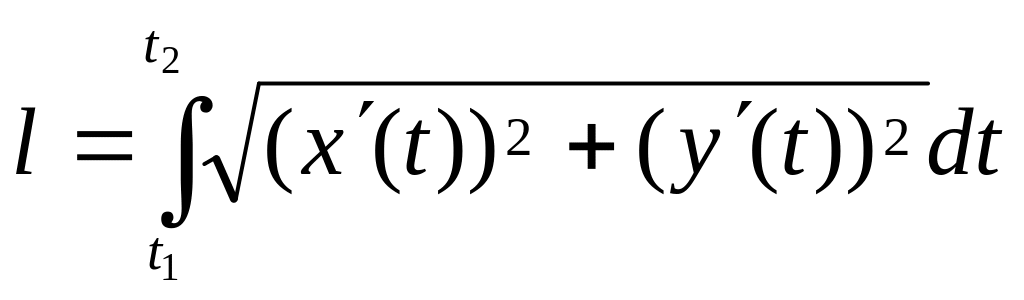 ; б)
; б)
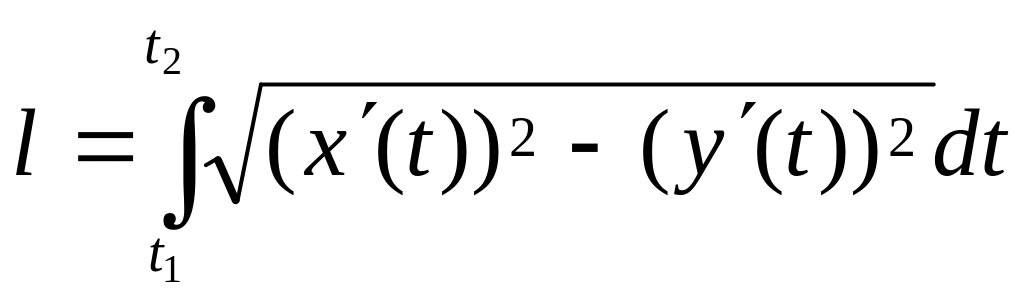 ;
;
в)
 ; г)
; г)
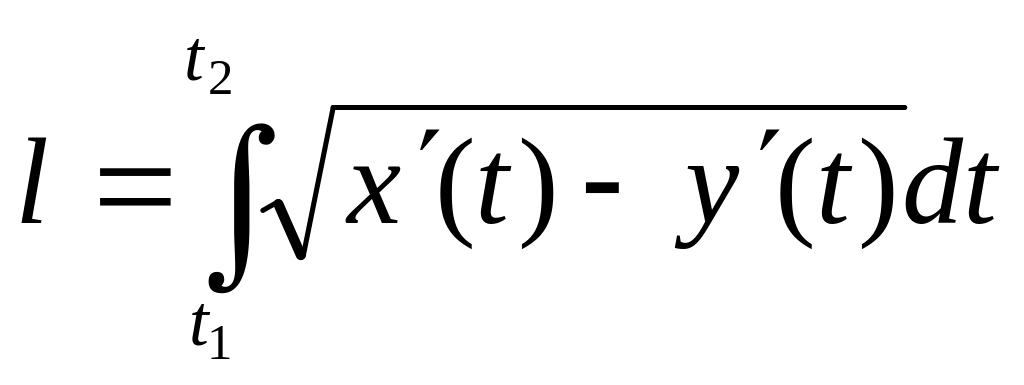 .
.
Якщо гладка крива задана в полярній системі координат рівнянням ,
 ,
то довжина дуги визначається за
формулою...
,
то довжина дуги визначається за
формулою...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Якщо криволінійна трапеція, обмежена кривою ( ) і прямими
 ,
,
,
обертається навколо осі
,
то об’єм тіла обертання обчислюється
за формулою...
,
,
,
обертається навколо осі
,
то об’єм тіла обертання обчислюється
за формулою...
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Якщо фігура обмежена кривими
 ,
,
 (
( )
і прямими
)
і прямими
 ,
обертається навколо осі
,
то об’єм тіла обертання визначається
за формулою...
,
обертається навколо осі
,
то об’єм тіла обертання визначається
за формулою...
а)![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Основна властивість визначеного інтеграла – це...
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
”ДОСЛІДЖЕННЯ НА ЗБІЖНІСТЬ ЧИСЛОВИХ РЯДІВ”
Числовим нескінченим рядом називають символічний вираз вигляду...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Необхідною ознакою збіжності числового ряду є...
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
Числовий ряд називають збіжним, якщо...
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
Гармонічним називають ряд...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Для збіжного ряду
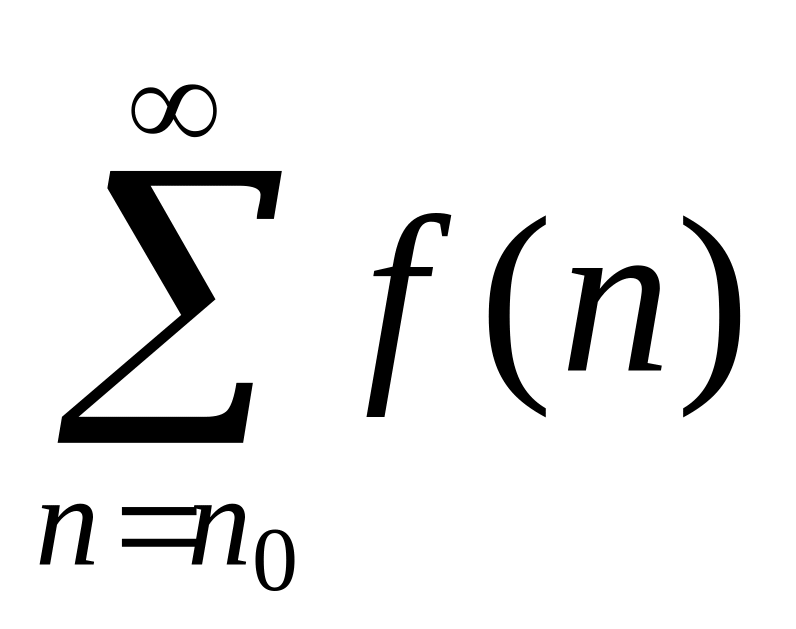 інтегральна ознака Коші має вигляд...
інтегральна ознака Коші має вигляд...
а)
![]() ,
,
![]() ; б)
; б)
![]() ;
;
в)
![]() ,
,
![]() ; г)
,
; г)
,
![]() .
.
Для збіжного ряду
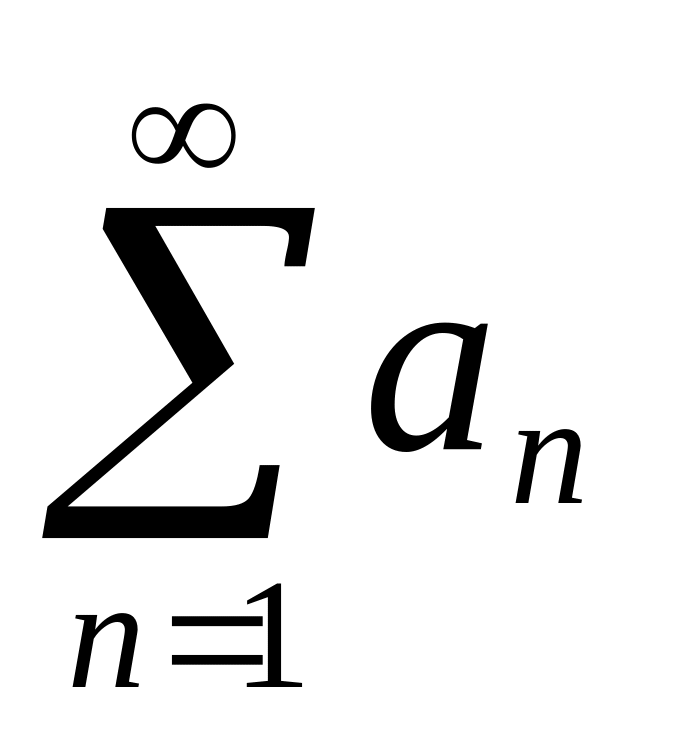 ознака Коші має вигляд...
ознака Коші має вигляд...
а)
![]() ,
,
![]() ; б)
,
; б)
,
![]() ;
;
в)
![]() ,
; г)
,
.
,
; г)
,
.
Для збіжного ряду ознака Даламбера має вигляд...
а)
![]() ,
; б)
,
;
,
; б)
,
;
в)
![]() ,
; г)
,
.
,
; г)
,
.
Геометричним називають ряд...
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Геометричний ряд
 збіжний при...
збіжний при...
а)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
Узагальнений гармонічний ряд
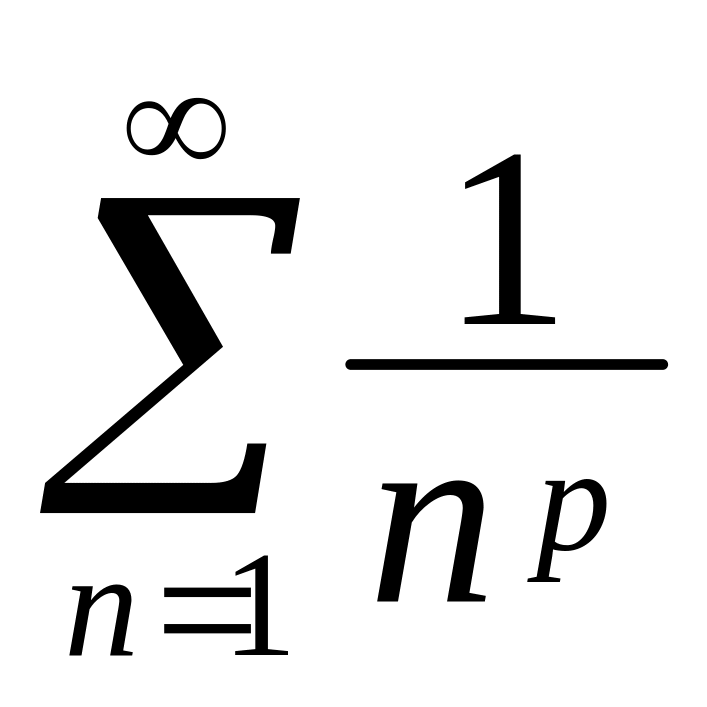 збіжний при...
збіжний при...
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() ; г)
; г)
![]() .
.
Нехай і
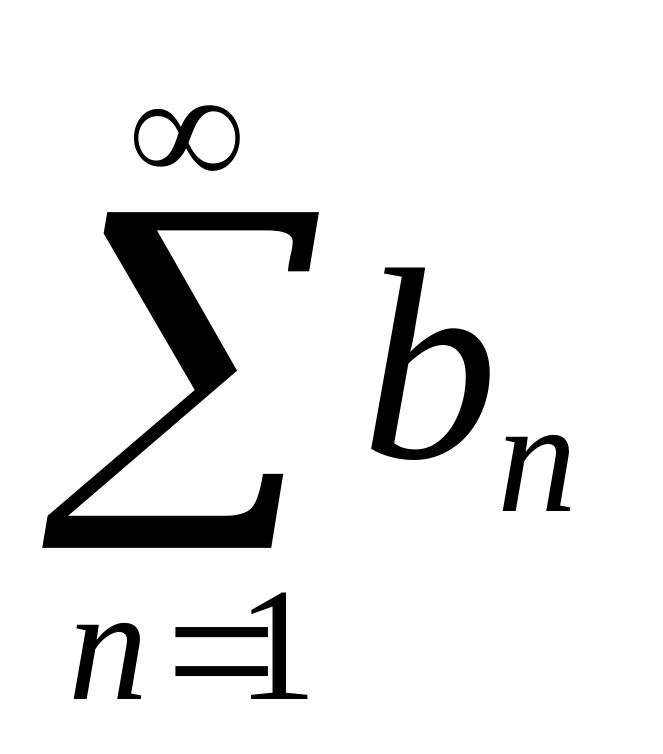 знакододатні ряди, причому
знакододатні ряди, причому
 для всіх
для всіх
 .
Тоді...
.
Тоді...
а) якщо ряд збігається, то ряд також збігається;
б) якщо ряд збігається, то ряд розбігається;
в) якщо ряд збігається, то ряд також збігається;
г) якщо ряд збігається, то ряд розбігається.
Нехай і знакододатні ряди, причому для всіх . Тоді...
а) якщо ряд розбігається, то й ряд розбігається;
б) якщо ряд розбігається, то ряд збігається;
в) якщо ряд збігається, то ряд розбігається;
г) якщо ряд збігається, то ряд збігається.
