”Операції над множинами”
Під поняттям множини розуміють...
а) сукупність деяких відмінних один від одного об’єктів або предметів, об’єднаних за певною ознакою в єдине ціле;
б) сукупність деяких відмінних один від одного об’єктів або предметів, об’єднаних за деякими ознаками в єдине ціле;
в) сукупність деяких об’єктів або предметів, об’єднаних за певною ознакою в єдине ціле;
г) сукупність деяких відмінних один від одного об’єктів або предметів, об’єднаних в єдине ціле.
Множину
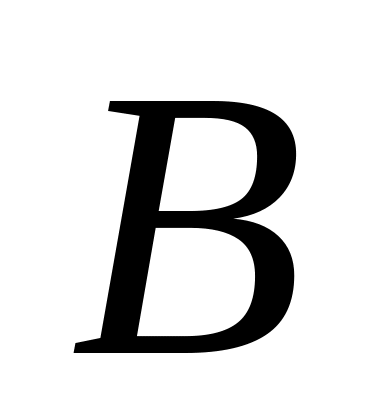називають підмножиною
множини
і записують
(або
),
якщо...
а)
; б)
;
в)
; г)
.
Перерізом множин і називають множину
,
яка...
а)
і
; б)
і
;
в)
і
; г)
і
.
Об’єднанням множин і називають множину
,
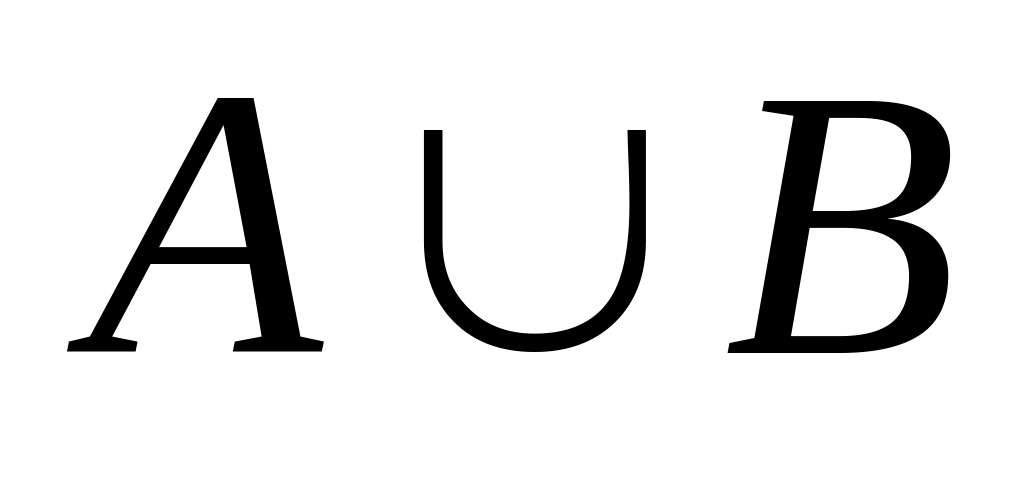яка...
а)
або
; б)
або
;
в) або ; г) або .
Різницею множин і називають множину \ , яка...
а)
\
і
; б)
\
і
;
в) \ і ; г) \ і .
Декартовим добутком не порожніх множин і називають множину
,
яка...
а)
і
; б)
і
;
в)
і
; г)
і
.
На діаграмі Ейлера – Вена зображено...
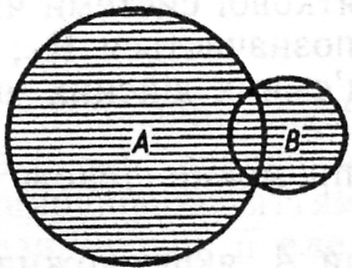
а) об’єднання множин і ; б) переріз множин і ;
в) різниця множин і ; г) декартовий добуток множин і .
На діаграмі Ейлера – Вена зображено...
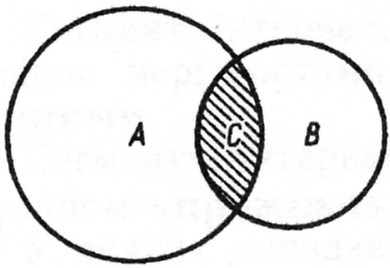
а) переріз множин і ; б) об’єднання множин і ;
в) різниця множин і ; г) декартовий добуток множин і .
На діаграмі Ейлера – Вена зображено...
а) різниця множин і ; б) переріз множин і ;
в) об’єднання множин і ; г) декартовий добуток множин і .
Множини і називають рівними і записують
,
якщо...
а)
і
; б)
і
; в)
і
; г)
і
.
Закон де Моргана має вигляд...
а)
; б)
; в)
; г)
.
Закон де Моргана має вигляд...
а)
; б)
; в)
; г)
.
”Обчислення границі числової послідовності
Та функції”
Число
називається границею числової
послідовності
,
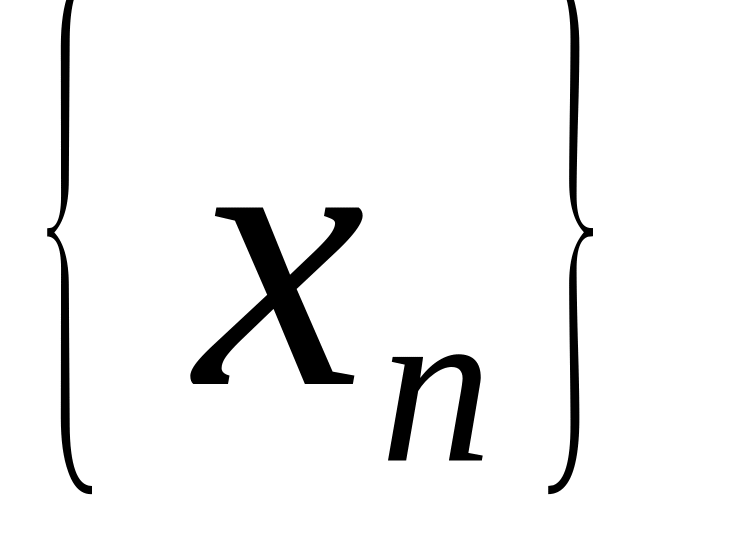якщо...
а) для будь – якого
існує (залежне від
)
число
таке, що виконується нерівність
для всіх (натуральних)
;
б) для будь – якого
існує (залежне від
)
число
таке, що виконується нерівність
для всіх (натуральних)
;
в) для будь – якого
існує (залежне від
)
число
таке, що виконується нерівність
для всіх (натуральних)
;
г) для будь – якого
існує (залежне від
)
число
таке, що виконується нерівність
для всіх (натуральних)
.
Числову послідовність називають нескінченно малою, якщо...
а)
; б)
; в)
; г)
.
Числову послідовність називають нескінченно великою, якщо...
а) ; б) ; в) ; г) .
Добуток нескінченно малої послідовності на обмежену є...
а) нескінченно малою послідовністю;
б) нескінченно великою послідовністю;
в) обмеженою послідовністю;
г) не обмеженою послідовністю.
Послідовність
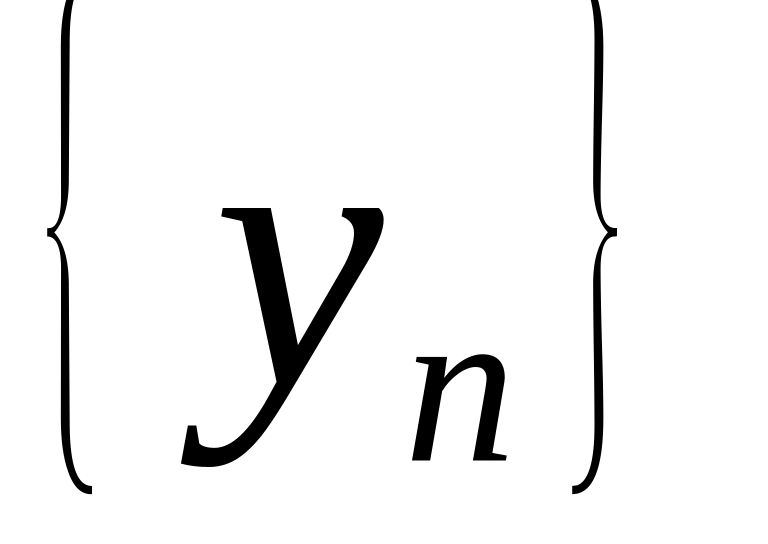називається обмеженою зверху, якщо...
а) існує таке число
,
що для всіх
;
б) існує таке число
,
що для всіх
;
в) існує таке число
,
що для всіх
;
г) існує таке число
,
що для всіх
.
Послідовність називається обмеженою знизу, якщо...
а) існує таке число
,
що для всіх
;
б) існує таке число
,
що для всіх
;
в) існує таке число
,
що для всіх
;
г) існує таке число
,
що для всіх
.
Означенням скінченої границі функції при
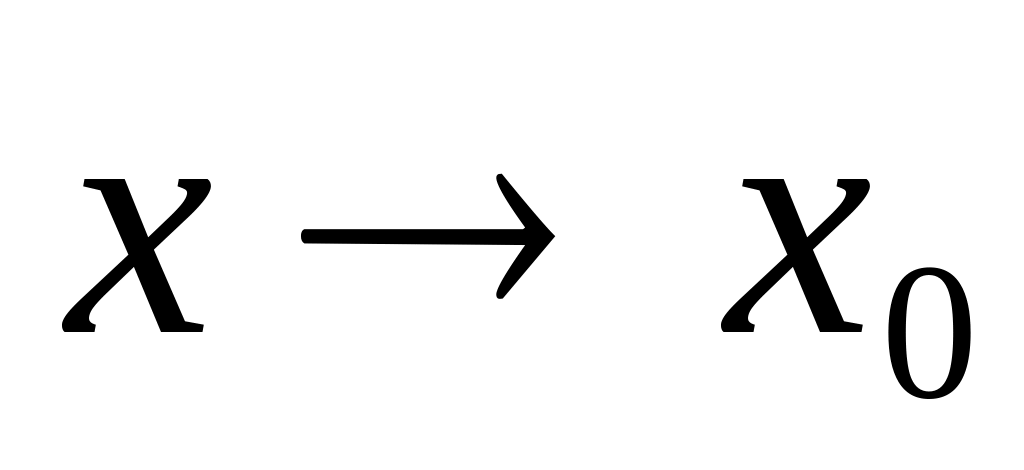на мові послідовностей (за Гейне) є...
а)
;
б)
;
в)
;
г)
.
Означенням скінченої границі функції при на мові „ -
”
(за Коші) є...
а) ;
б) ;
в) ;
г) .
Перша важлива границя має вигляд...
а)
; б)
; в)
; г)
.
Друга важлива границя має вигляд...
а) ; б) ; в) ; г) .
Якщо
,
– нескінченно малі функції, то вони
називаються нескінченно малими
однакового порядку малості, якщо...
а)
; б)
; в)
г)
.
Якщо , – нескінченно малі функції, то вони називаються еквівалентними, якщо...
а)
; б)
; в)
; г)
.
”Обчислення похідної та диференціалів функції”
Похідною функції
у довільній фіксованій точці
називається...
а)
;
б)
;
в)
;
г)
.
Рівняння дотичної до графіка функції у точці
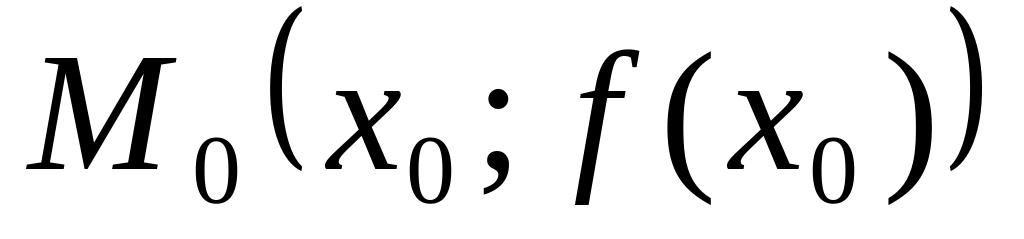має вигляд...
а)
; б)
;
в)
; г)
.
Рівняння нормалі до графіка функції у точці має вигляд...
а)
; б)
;
в)
; г)
.
Похідна суми двох функцій
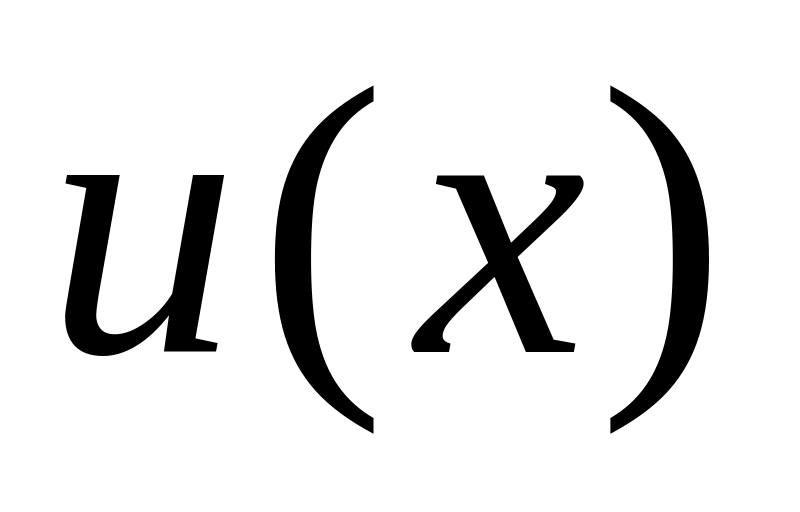та
дорівнює...
а)
; б)
;
в)
; г)
.
Похідна різниці двох функцій та дорівнює...
а)
; б)
;
в)
; г)
.
Похідна добутку двох функцій та дорівнює...
а)
;
б)
;
в)
;
г)
.
Похідна частки двох функцій та дорівнює...
а)
; б)
;
в)
; г)
.
Похідна складеної функції обчислюється за формулою...
а)
; б)
;
в)
; г)
.
Логарифмічна похідна функції
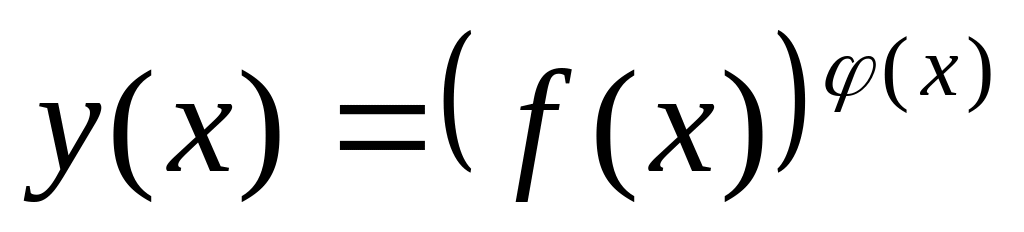обчислюється
за формулою...
а)
;
б)
;
в)
;
г)
.
Похідна функції
заданої параметрично
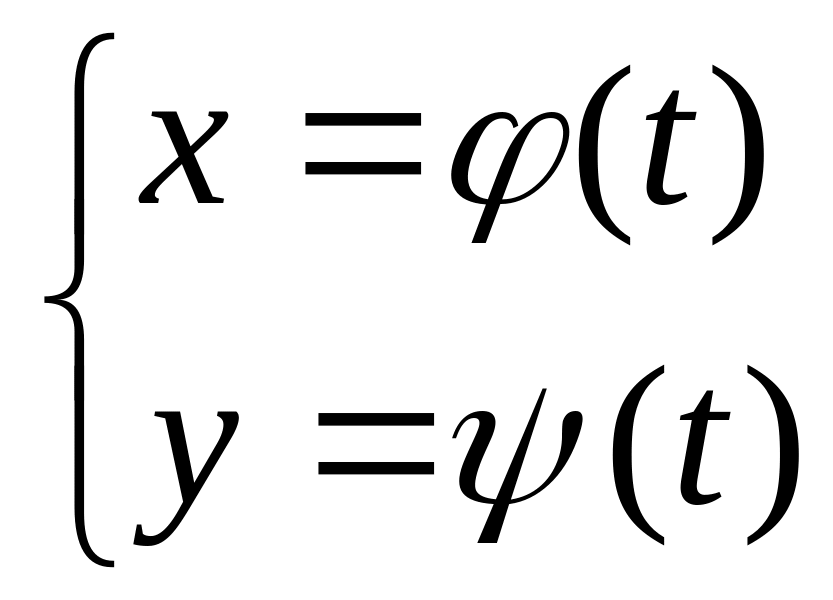обчислюється за формулою...
а)
; б)
; в)
; г)
.
Диференціал функції дорівнює...
а)
; б)
; в)
; г)
.
Диференціал функції застосовують до наближених обчислень у вигляді...
а)
; б)
;
в)
; г)
.
”Повне дослідження функції та побудова її графіка”
Функція зростає на інтервалі
,
якщо...
а)
; б)
; в)
; г)
.
Функція спадає на інтервалі , якщо...
а) ; б) ; в) ; г) .
Точка називається стаціонарною, якщо...
а)
; б)
; в)
; г)
.
В точці функція має мінімум, якщо
і...
а) при переході аргументу через точку похідна змінює свій знак з „-” на „+”;
б) при переході аргументу через точку похідна змінює свій знак з „+” на „-”;
в)
;
г)
.
В точці функція має максимум, якщо і...
а) при переході аргументу через точку похідна змінює свій знак з „+” на „-”;
б) при переході аргументу через точку похідна змінює свій знак з „-” на „+”;
в) ;
г) .
Функція на інтервалі має опуклість вгору (крива опукла), якщо...
а)
; б)
; в)
; г)
.
Функція на інтервалі має опуклість вниз (крива угнута), якщо...
а) ; б) ; в) ; г) .
Якщо для функції у деякій точці
виконується рівність
або
не існує і при перебігу через точку
друга похідна
змінює знак, то точка з абсцисою
є...
а) точкою перегину функції ;
б) стаціонарною точкою функції ;
в) критичною точкою функції ;
г) екстремальною точкою функції .
Пряма
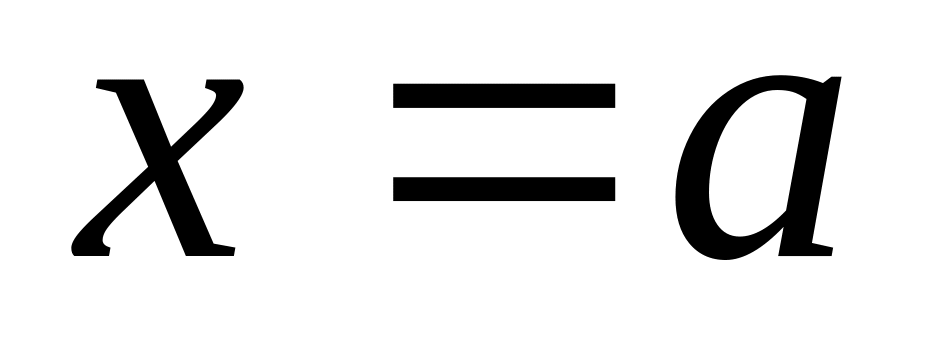є вертикальною асимптотою для функції
,
якщо...
а)
; б)
; в)
; г)
.
Кутовий коефіцієнт
похилої асимптоти
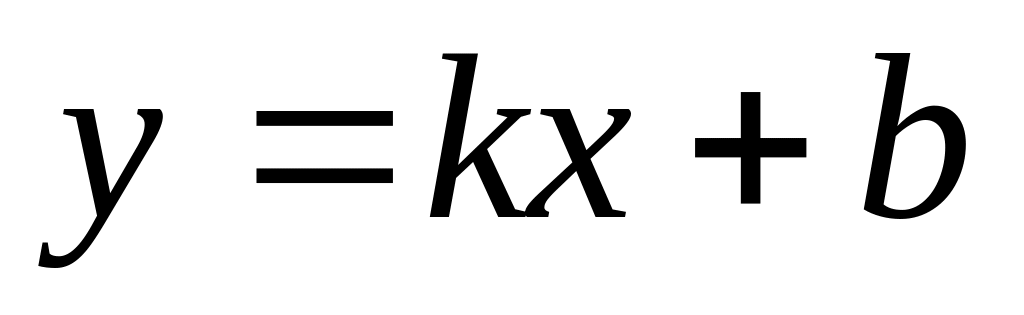для функції
знаходиться за формулою...
а)
;
б)
;
в)
;
г)
.
Початкова ордината
похилої асимптоти
для функції
знаходиться за формулою...
а)
; б)
;
в)
; г)
.
Екстремумами функції або екстремальними значеннями функції називають...
а) максимуми і мінімуми функції; б) точки перегину функції;
в) критичні точки функції; г) стаціонарні точки функції.