
Іі Розв’язати задачі:
Користуючись двома істотними границями та наслідками з них, обчислити границю
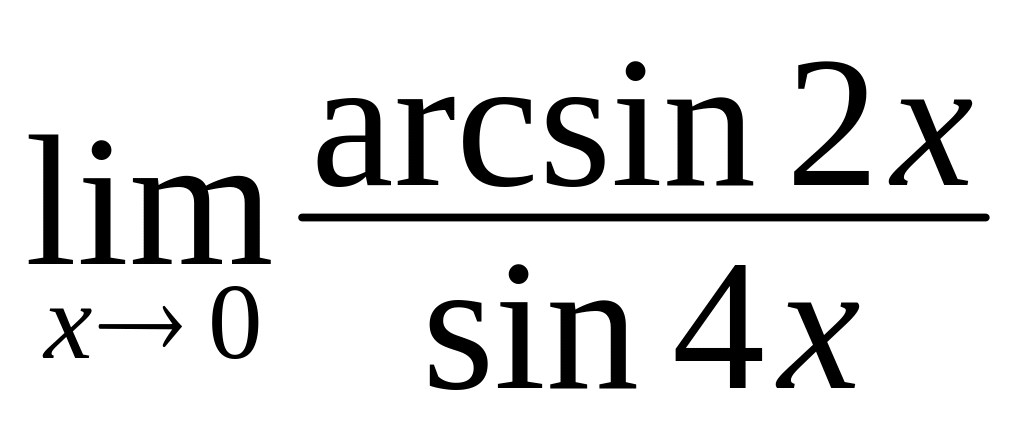 .
.Знайти масу пластини
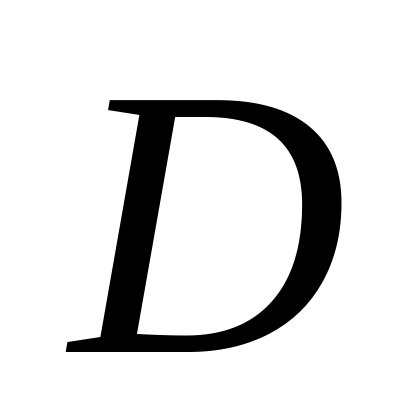 ,
заданої нерівністю
,
заданої нерівністю
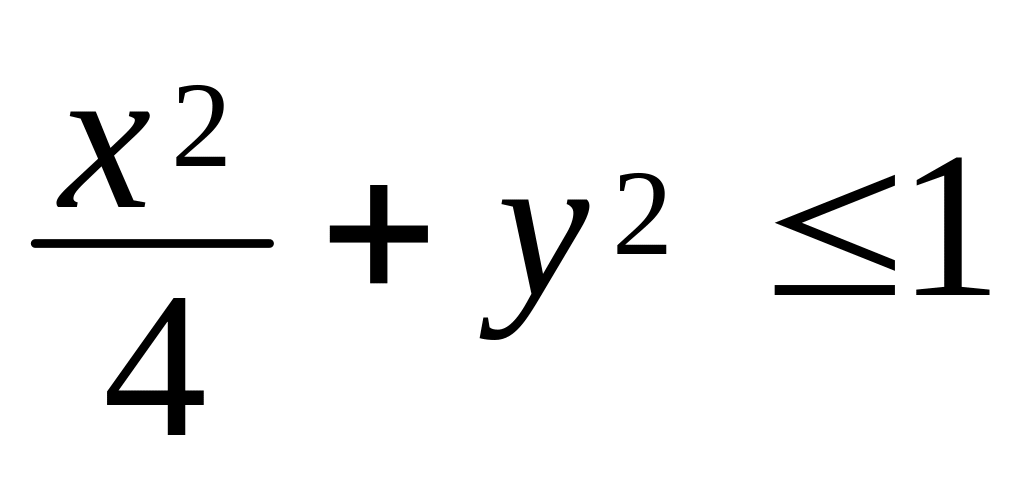 ,
з густиною
,
з густиною
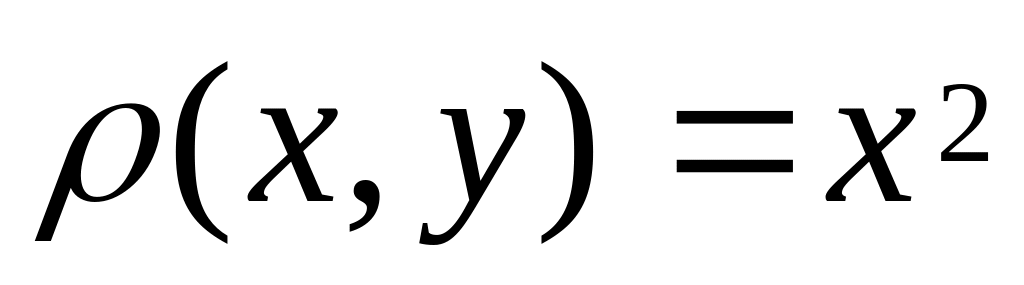 .
.Знайти інтеграл
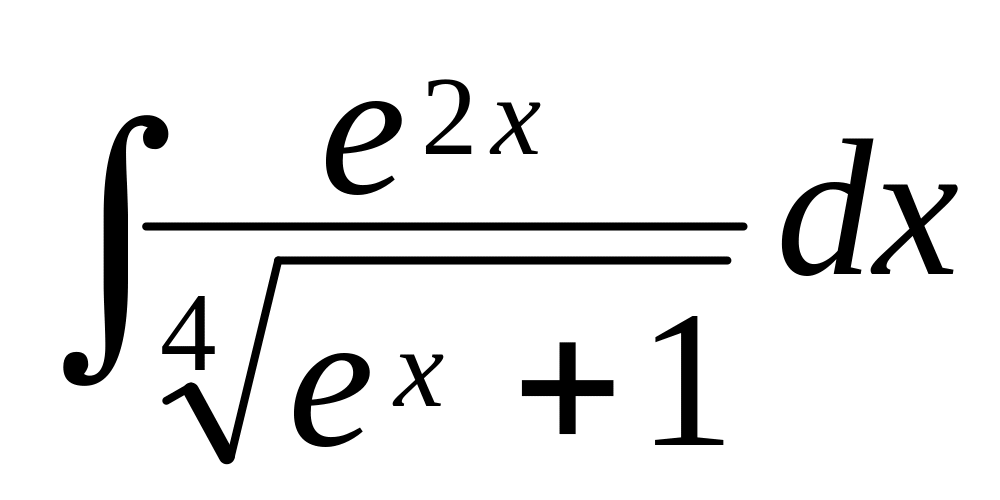 .
.Знайти радіус, інтервал та область збіжності даного степеневого ряду, дослідивши його поведінку на кінцях інтервалу збіжності
![]()
Дослідити на збіжність даний невласний інтеграл, та знайти його значення у випадку збіжності
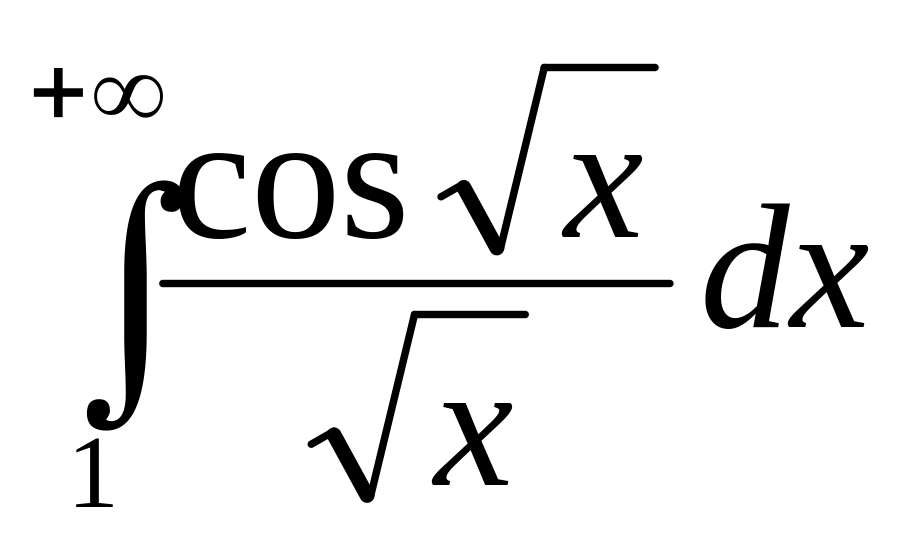 .
.Обчислити повторні границі
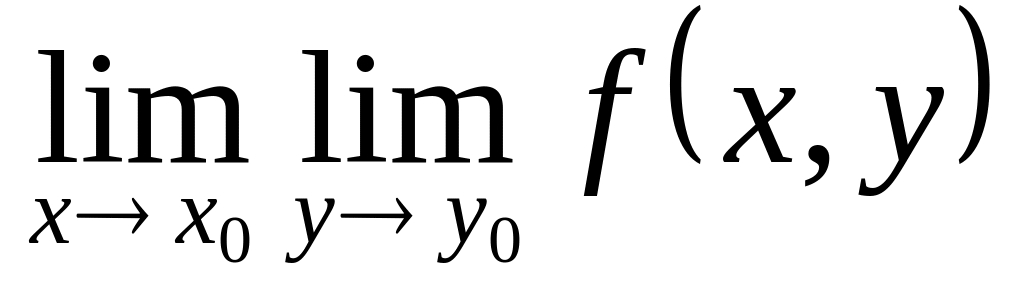 та
та
 ,
якщо
,
якщо
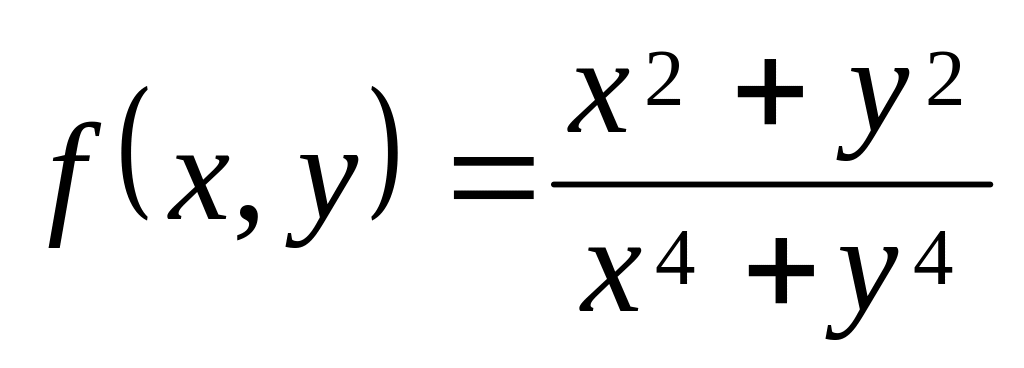 ,
,
![]() ,
,
![]() .
.
Знайти площу фігури, обмеженої параметрично заданою кривою
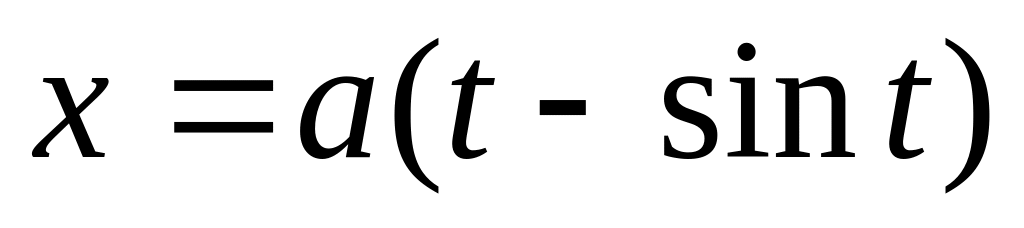 ,
,
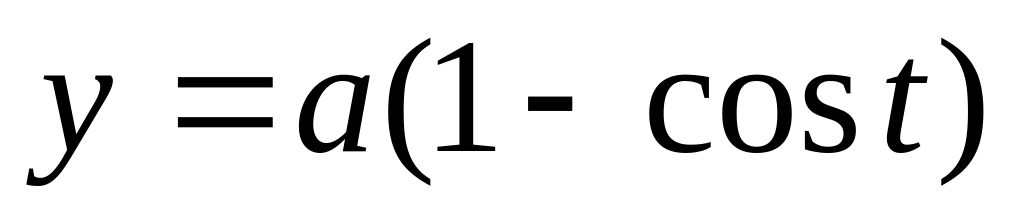 ;
;
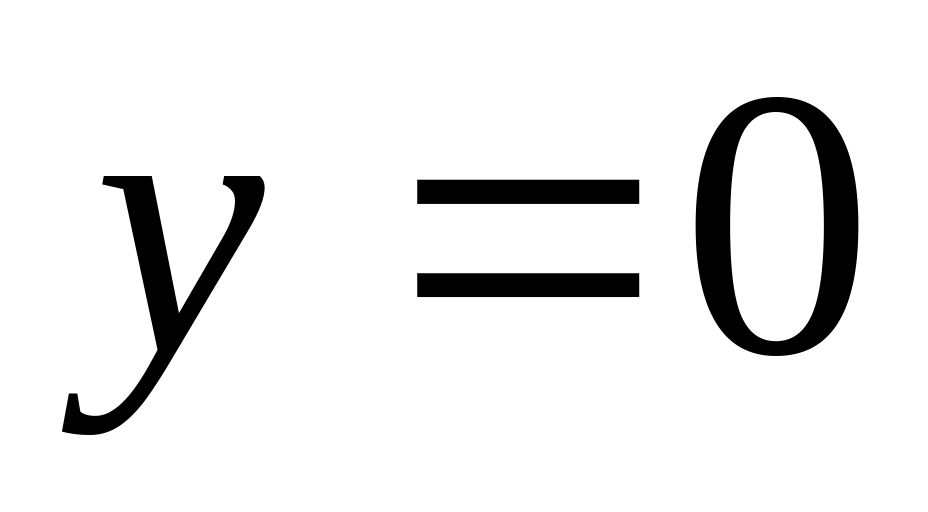 ,
,
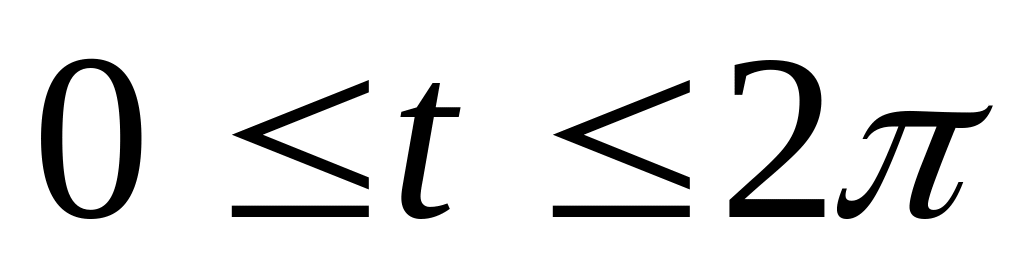 .
.Знайти похідну даної функції, заданої параметрично
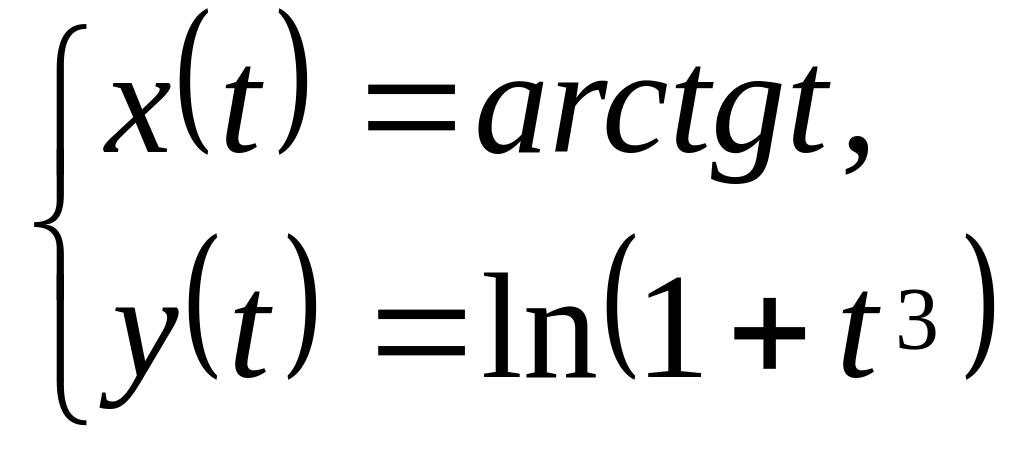 .
.Обчислити границю функції
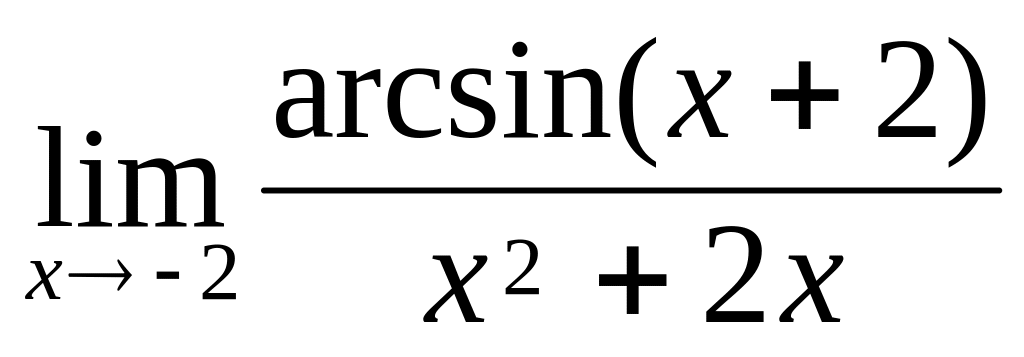 .
.Обчислити об’єм тіла, отриманого обертанням навколо осі
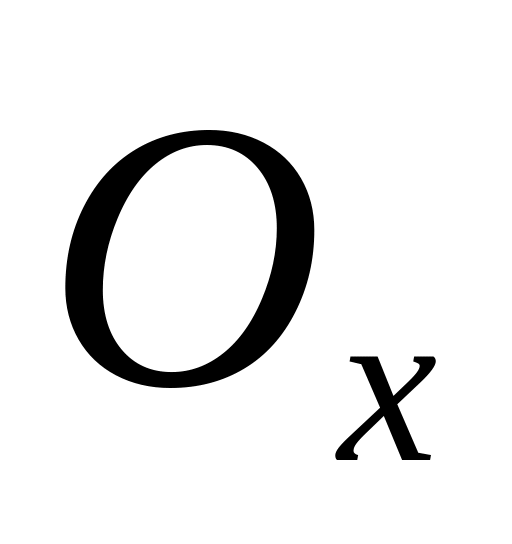 криволінійної трапеції, обмеженої
лініями
криволінійної трапеції, обмеженої
лініями
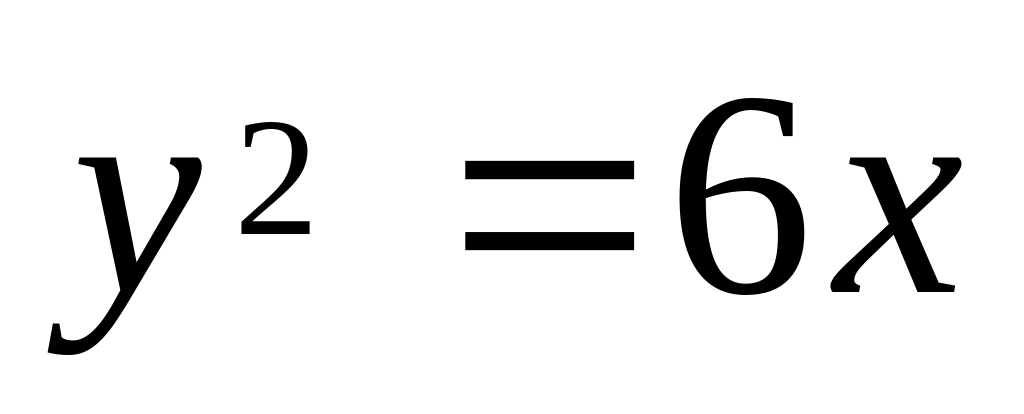 ,
,
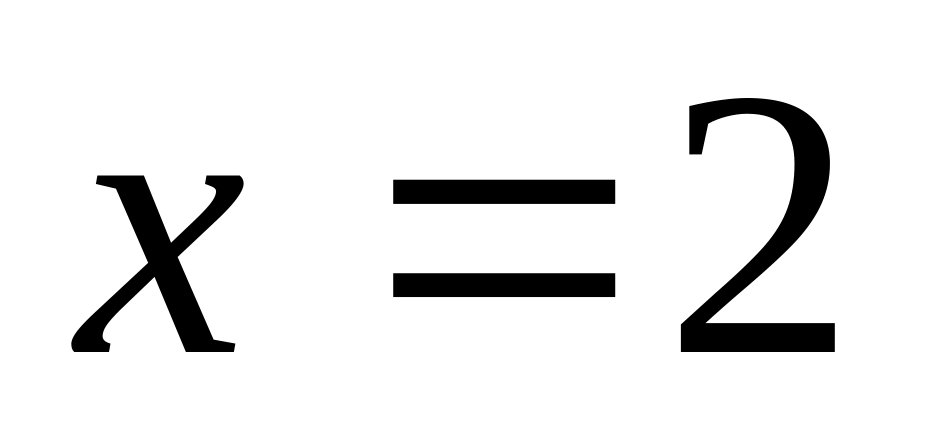 та віссю
та віссю
Довести дане твердження або показати, що воно є неправильним
(А|B)|C=(A|C)|(B|C).
Обчислити криволінійний інтеграл
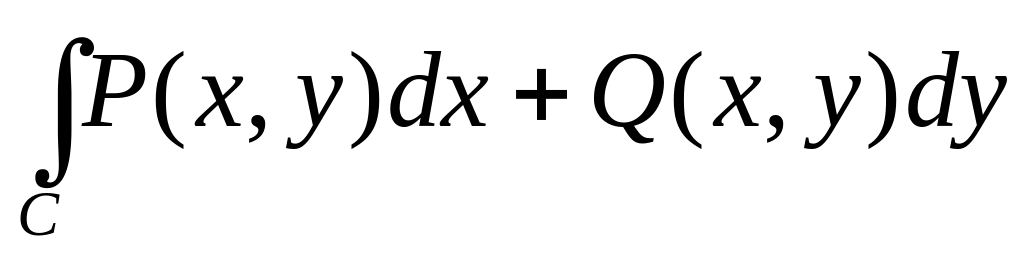 ,
якщо
,
якщо
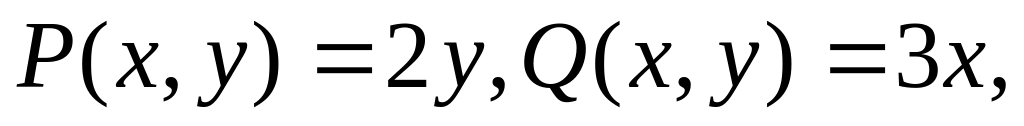
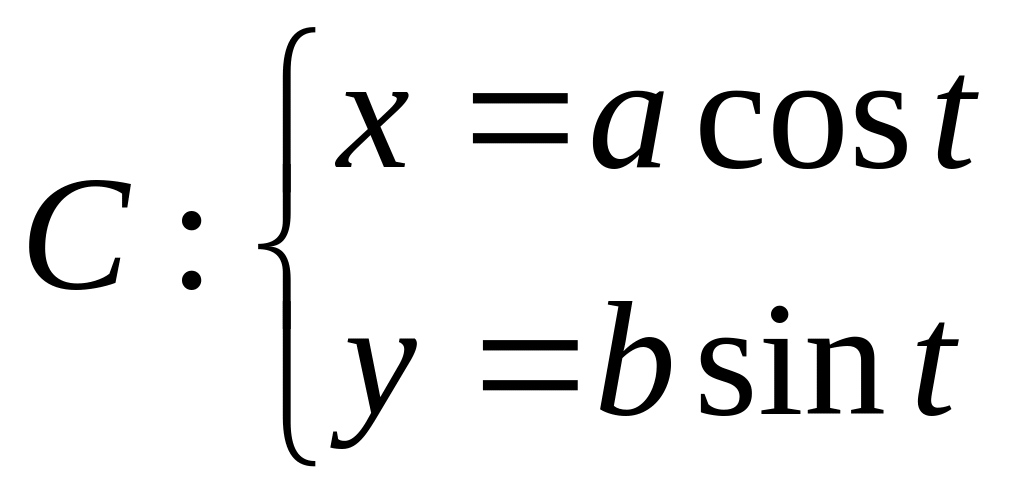 − від точки
− від точки
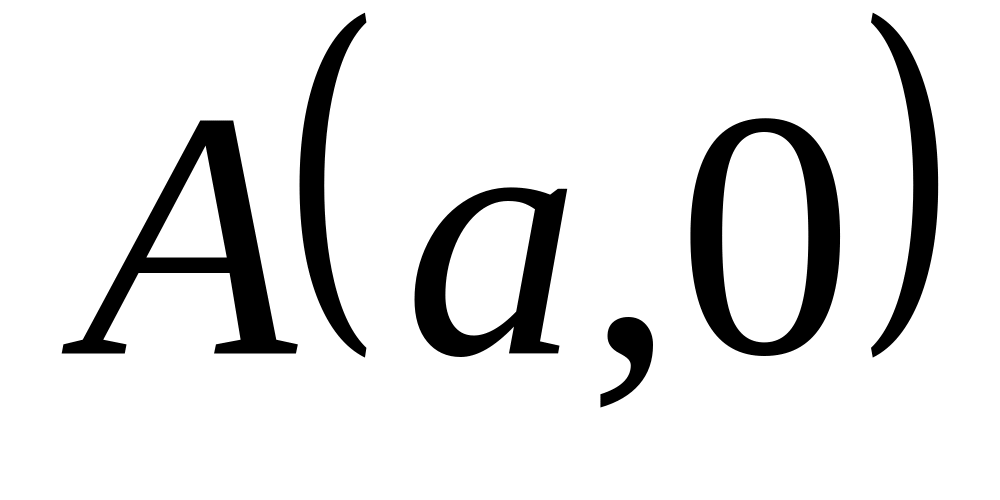 до точки
до точки
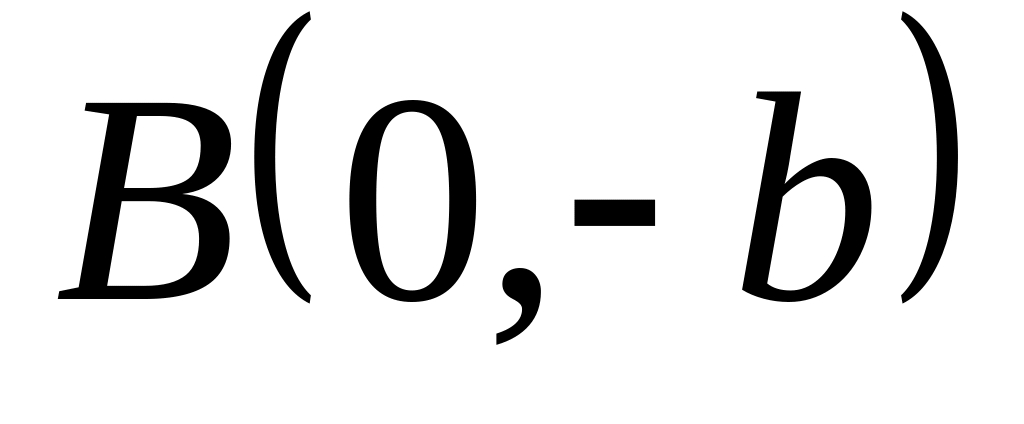 у від’ємному напрямку.
у від’ємному напрямку.Знайти об’єм тіла, яке утворюється при обертанні навколо осі
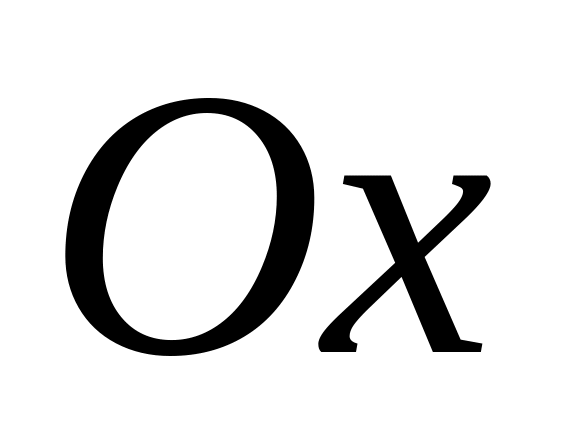 фігури, обмеженої заданими лініями
фігури, обмеженої заданими лініями
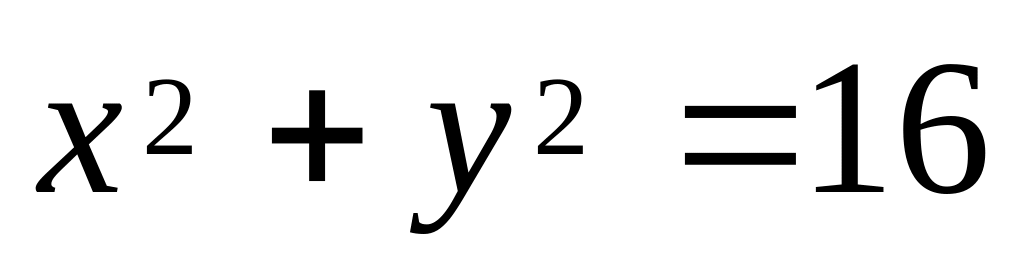 ,
,
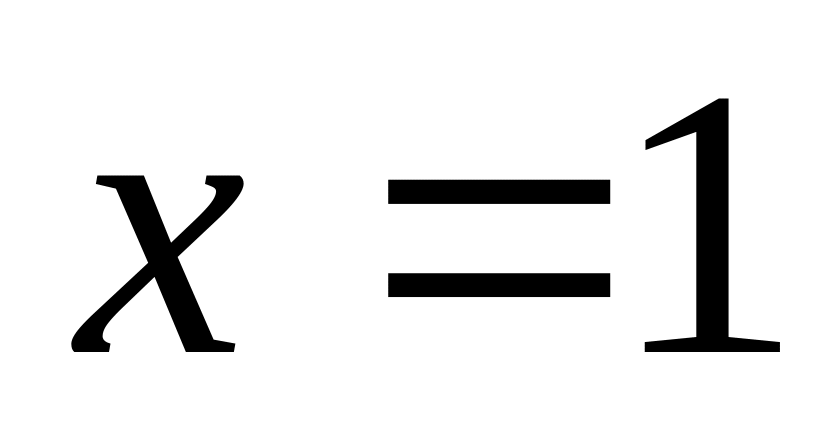 ,
,
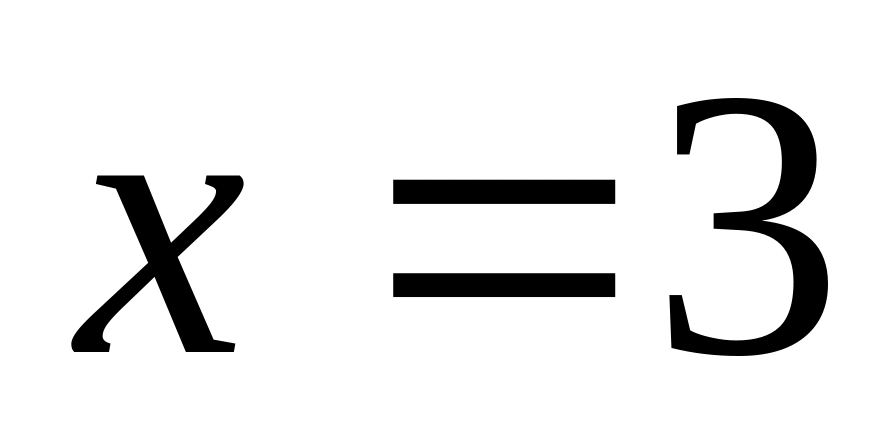 ,
,
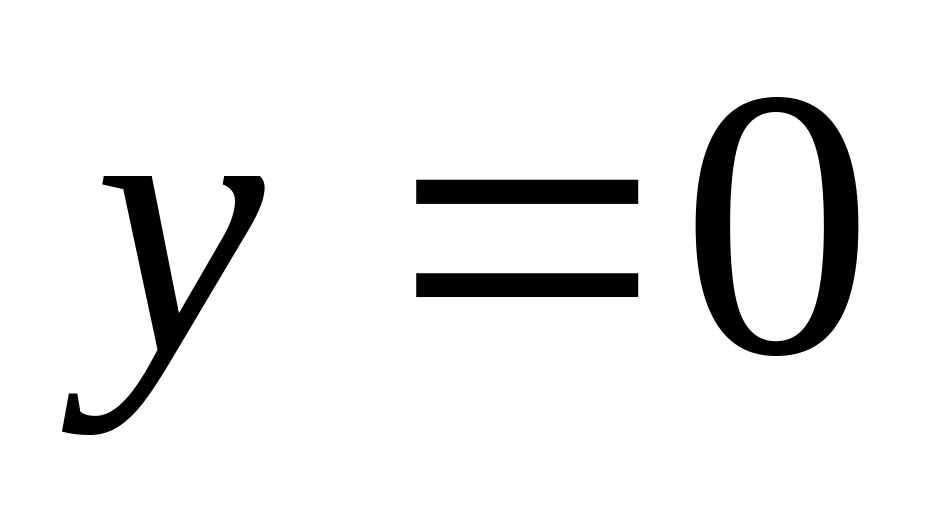 .
.Обчислити границю функції
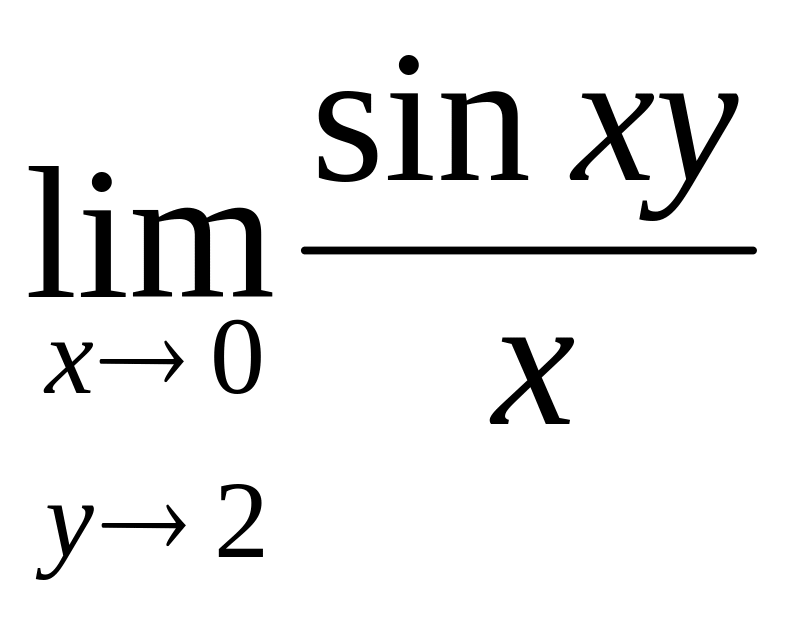 .
.Записати формулу Тейлора для функції
 за степенями
за степенями
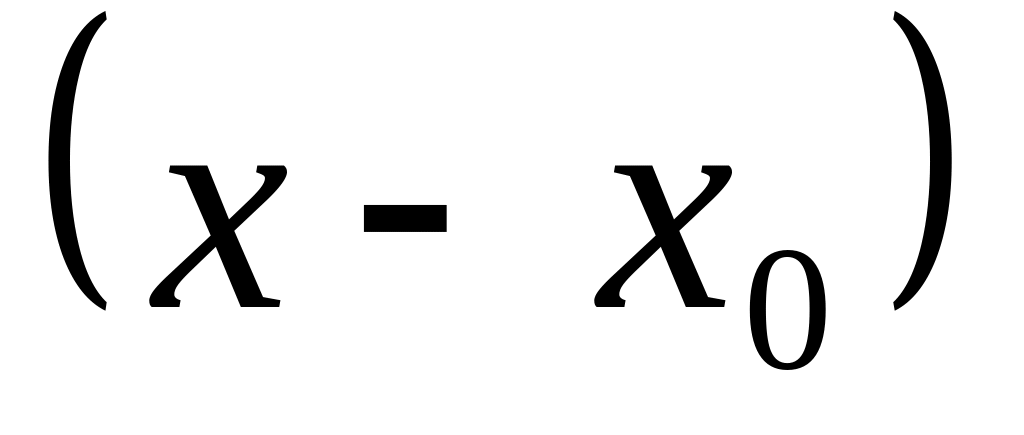 до члена з
до члена з
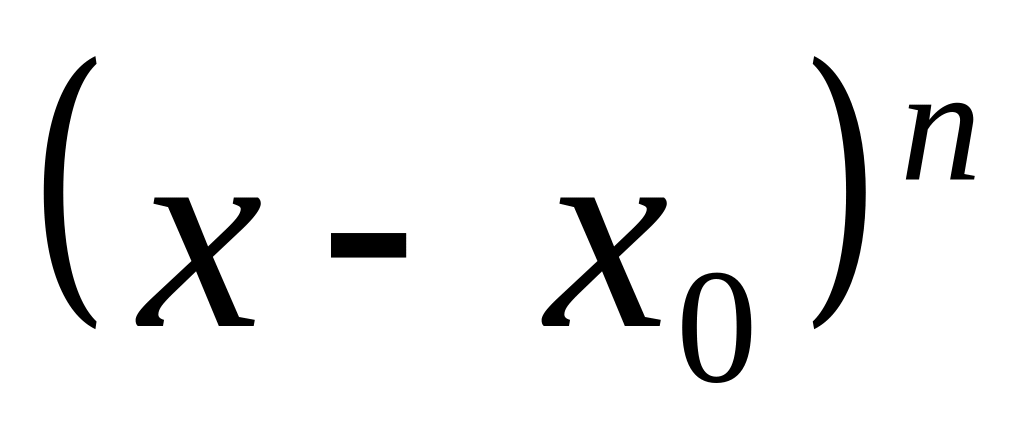 :
:
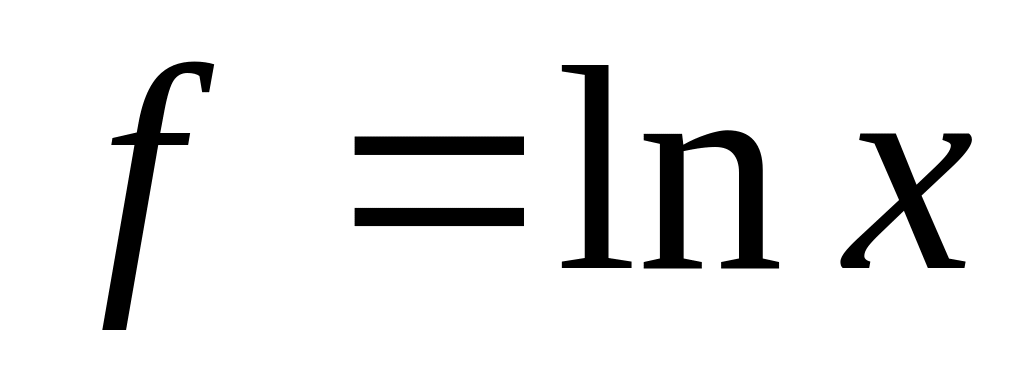 ,
,
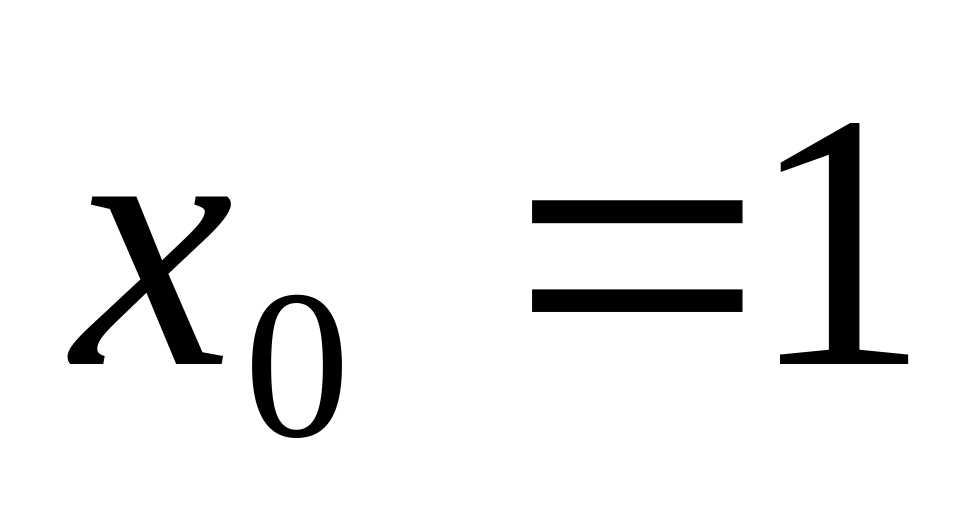 ,
,
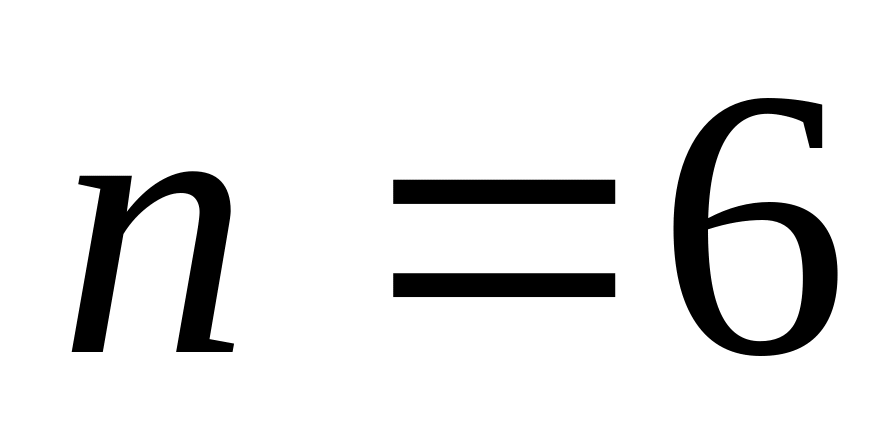 .
.Знайти та зобразити область визначення функції декількох змінних
![]()
Обчислити криволінійний інтеграл
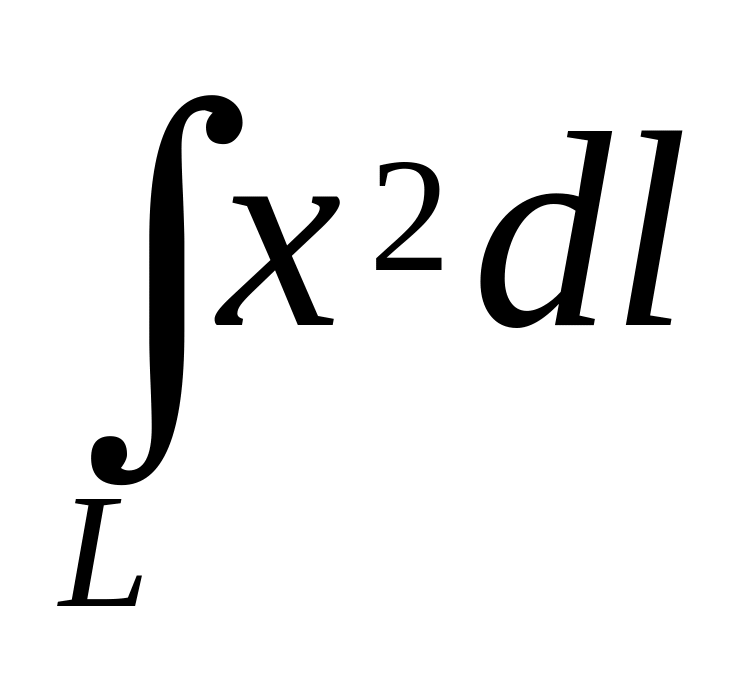 вздовж кривої
вздовж кривої
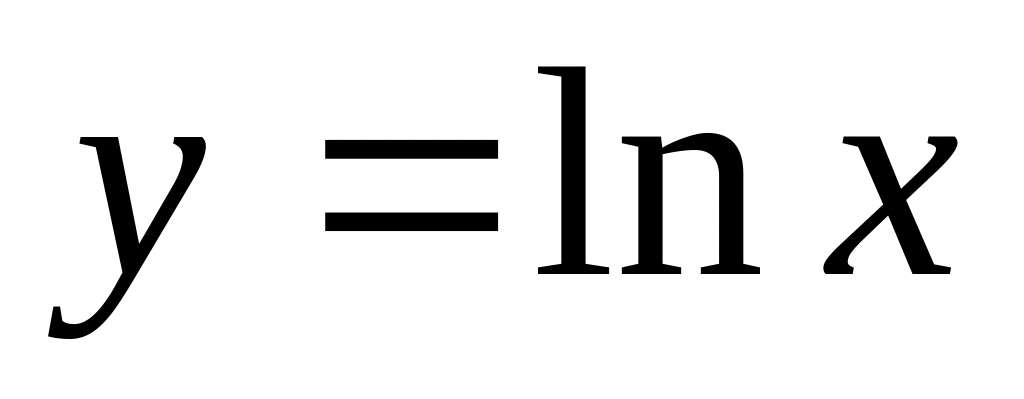 ,
кінці якої знаходяться в точках з
абсцисами
,
кінці якої знаходяться в точках з
абсцисами
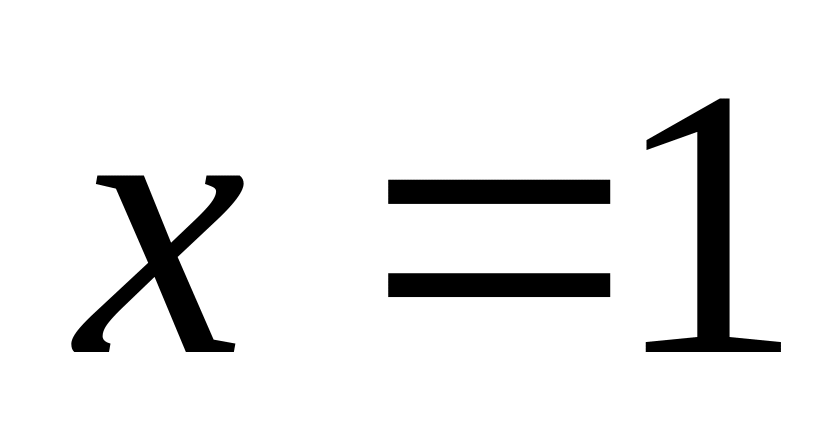 і
.
і
.Визначити інтервали неперервності функції, дослідити точки і характер розриву, та побудувати її графік
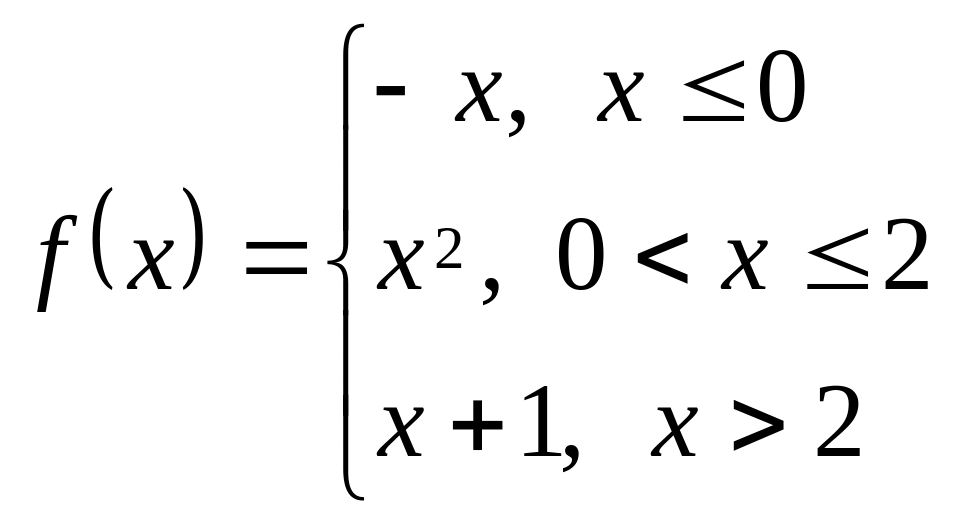
Обчислити границю функції
 .
.Поміняти порядок інтегрування. Область інтегрування зобразити на малюнку
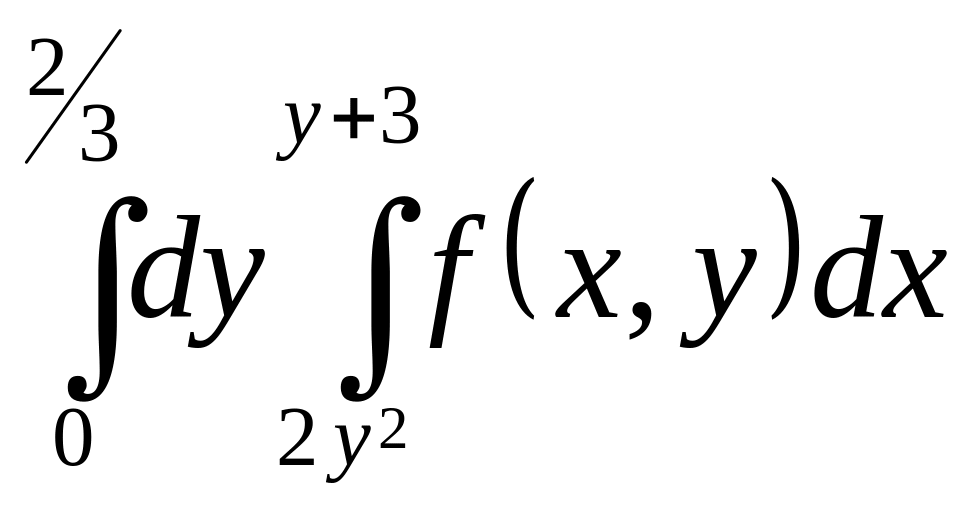 .
.Знайти похідну даної функції, заданої параметрично
![]() .
.
Обчислити подвійний інтеграл переходячи до полярних координат
![]() ,
,
![]()
![]() .
.
Знайти повторний інтеграл
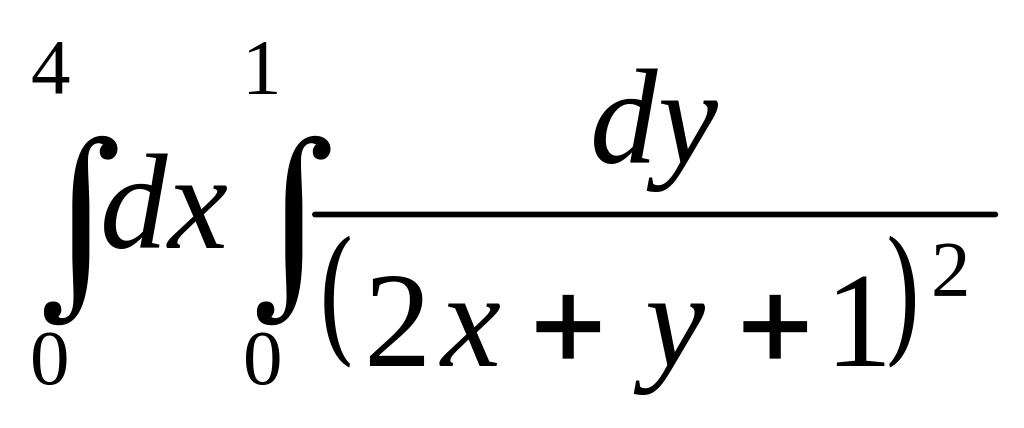 .
.Користуючись двома істотними границями та наслідками з них, обчислити дану границю
 .
.Дослідити на збіжність даний невласний інтеграл, та знайти його значення у випадку збіжності
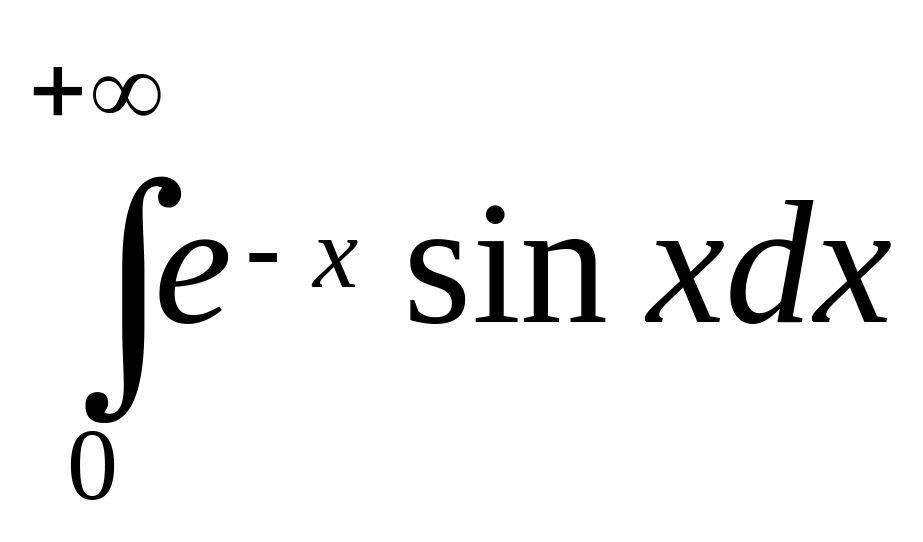 .
.Користуючись властивостями границь, обчислити дану границю
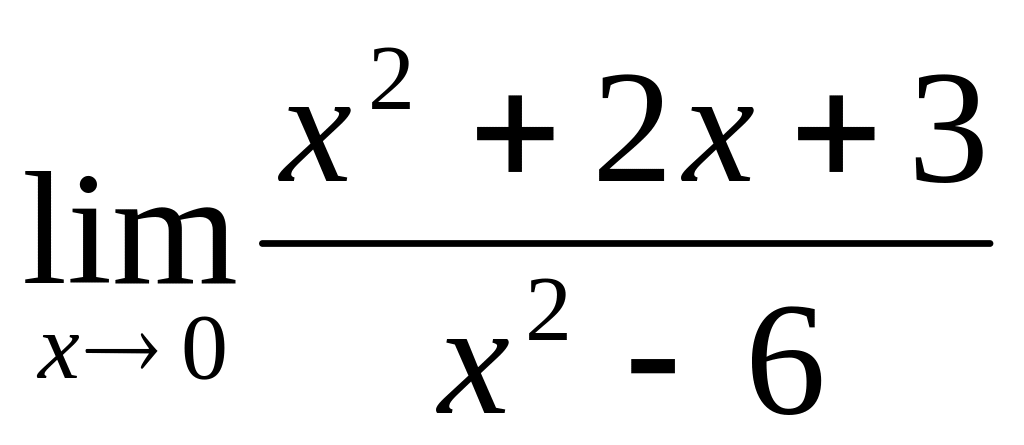 .
.Дослідити даний ряд на збіжність
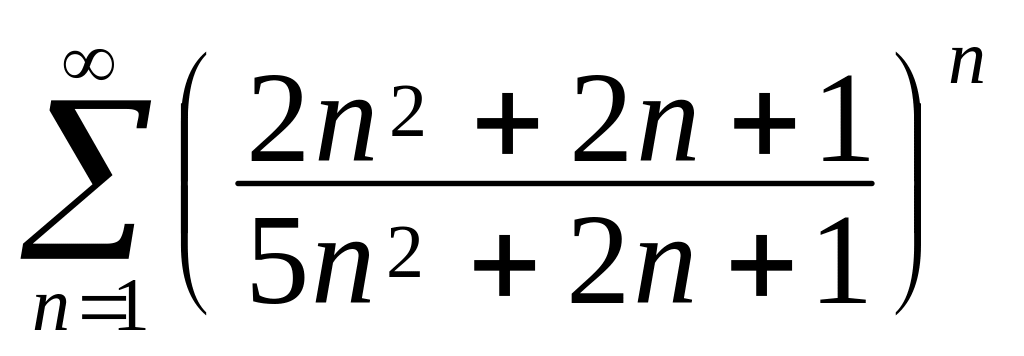 .
.Обчислити
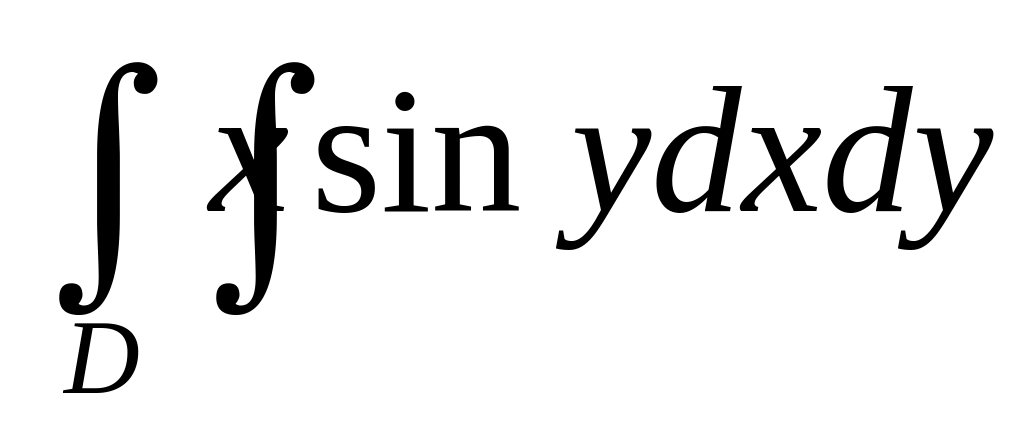 ,
якщо область
– прямокутник
,
якщо область
– прямокутник
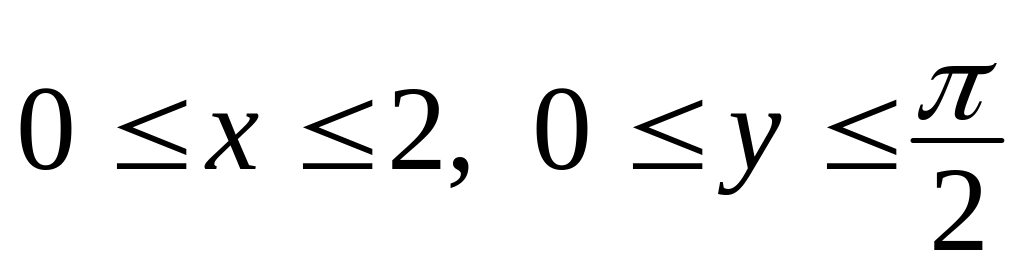 .
.Знайти об’єм тіла, яке утворюється при обертанні навколо осі
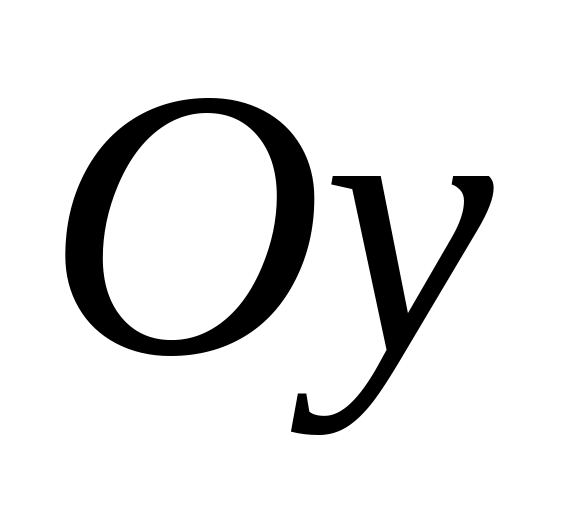 фігури, обмеженої заданими лініями
фігури, обмеженої заданими лініями
 ,
,
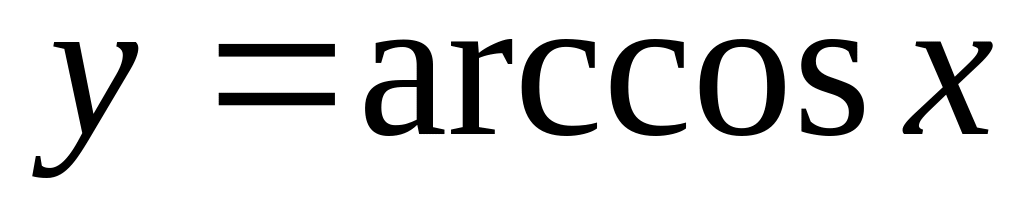 ,
.
,
.Обчислити границю функції
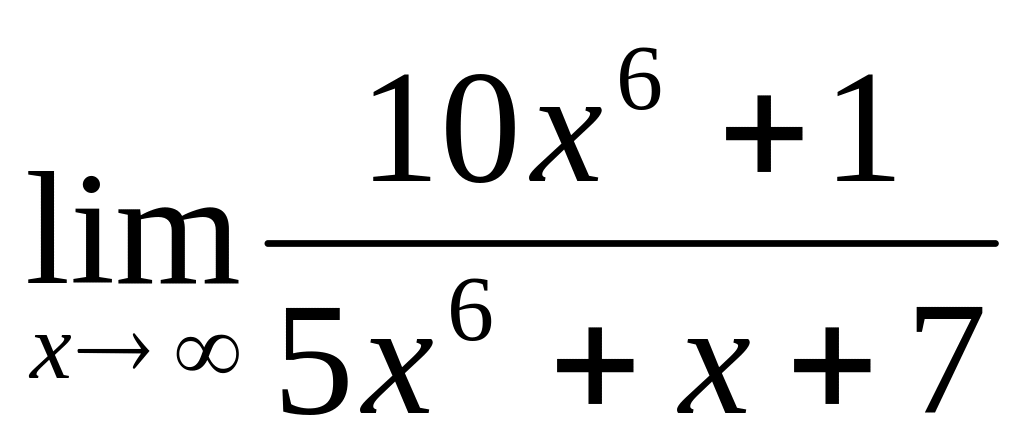 .
.Знайти інтеграл
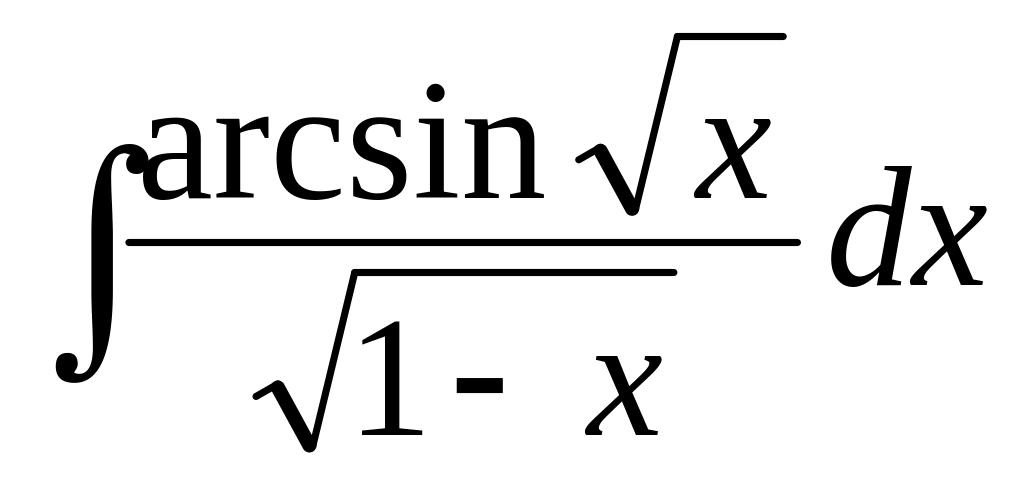 .
.Знайти область збіжності даного функціонального ряду
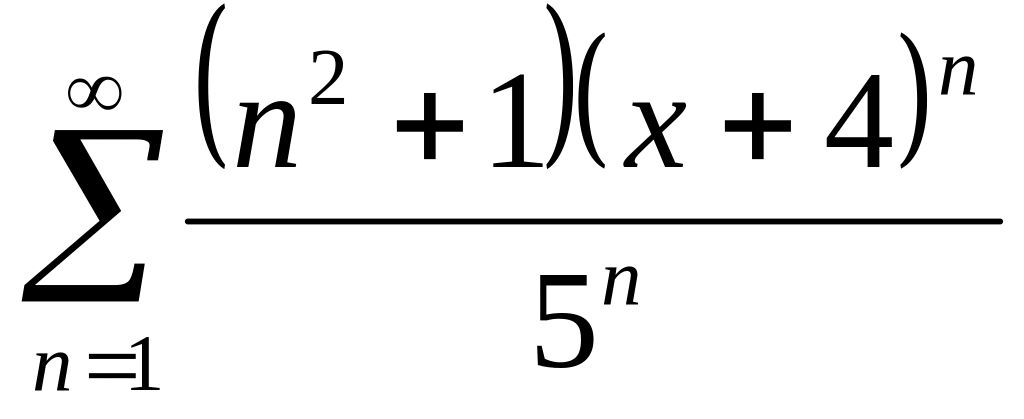 .
.Знайти градієнт функції
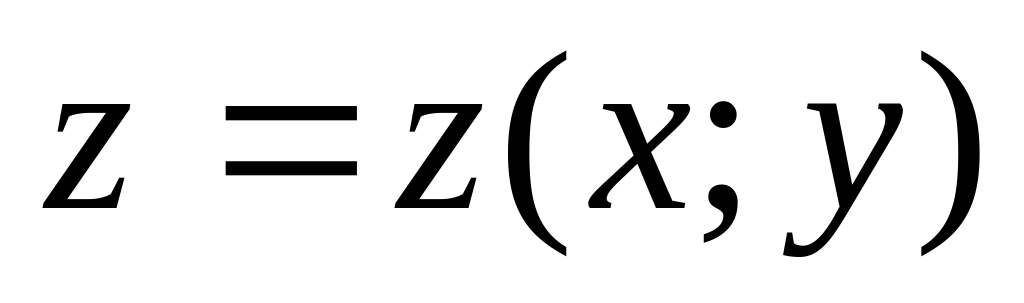 у точці
у точці
 ,
та похідну у точці
за напрямом вектора
,
та похідну у точці
за напрямом вектора
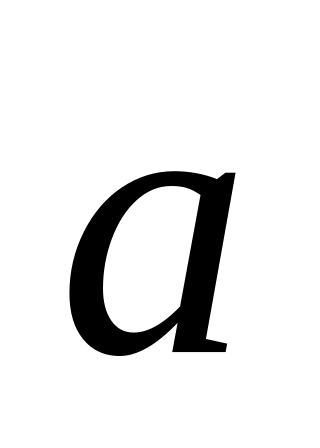 ,
якщо
,
якщо
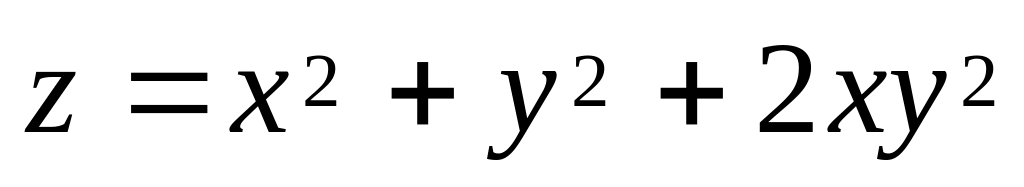 ,
,
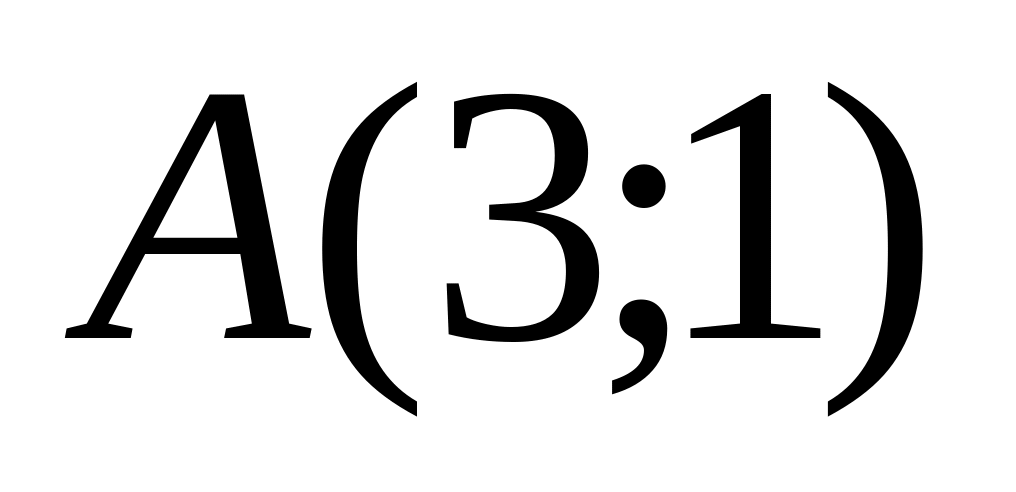 ,
,
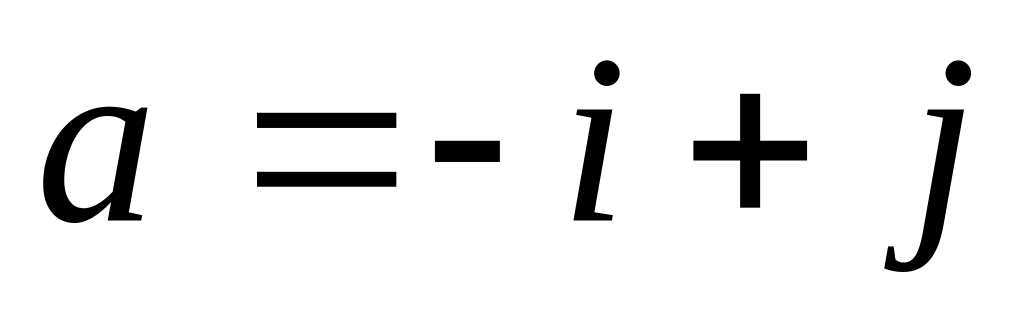 .
.Знайти даний інтеграл, скориставшись методом підстановки
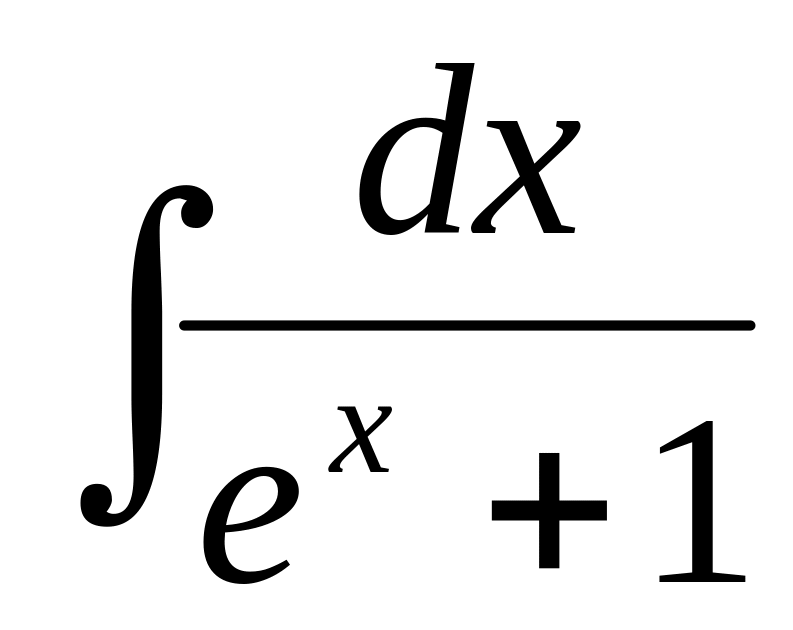 .
.Знайти координати центра мас даної однорідної матеріальної дуги , ,
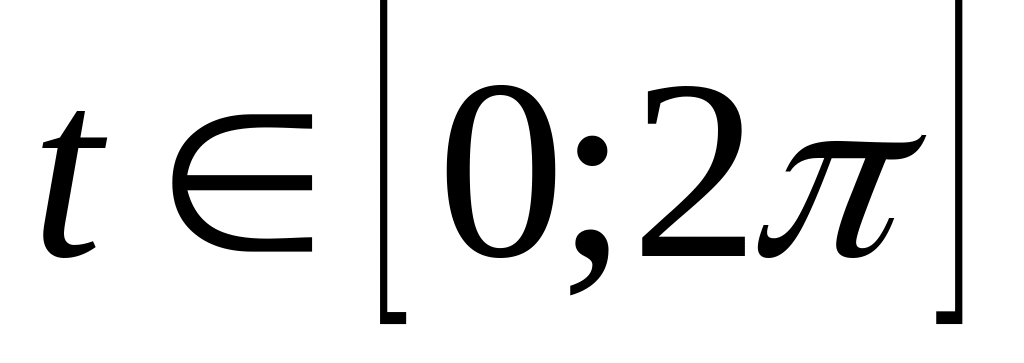 .
.За допомогою ознаки Коші дослідити збіжність рядів
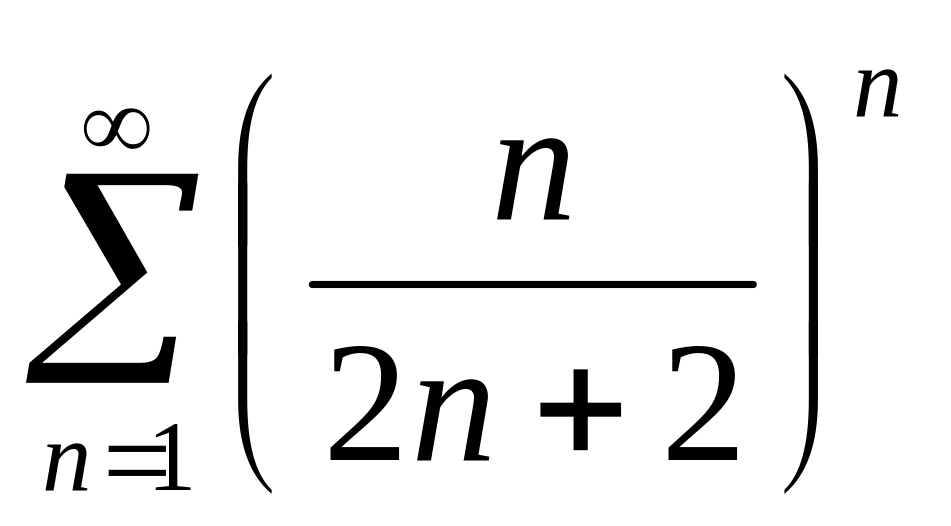 .
.Довести дане твердження або показати, що воно є неправильним: (A
 B)|B=A|B.
B)|B=A|B.Використовуя інтегральну ознаку Коші дослідити ряди на збіжність
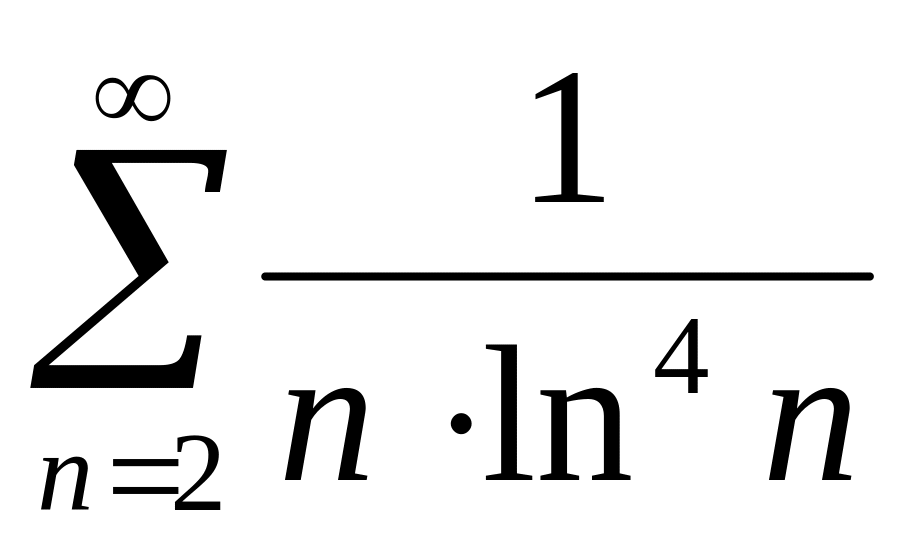 .
.Знайти інтеграл
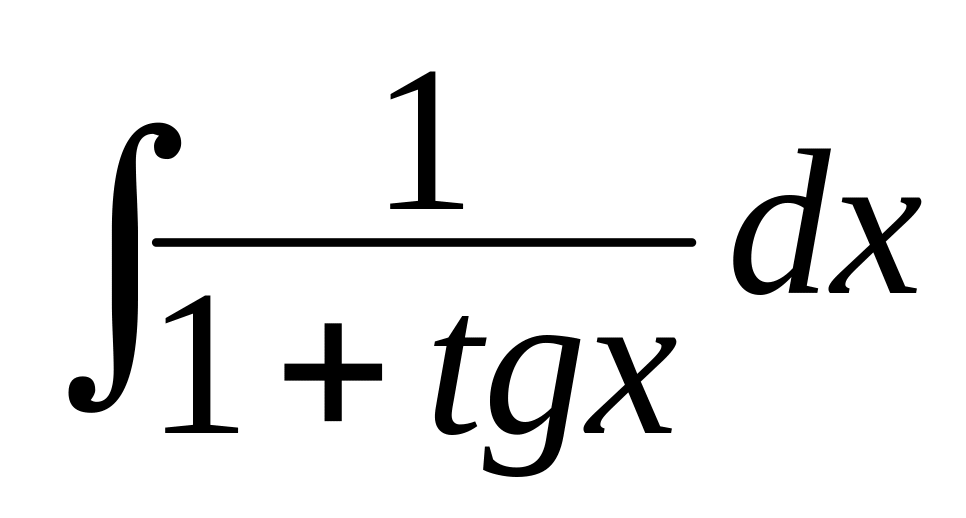 .
.За допомогою ознаки Коші дослідити збіжність ряду
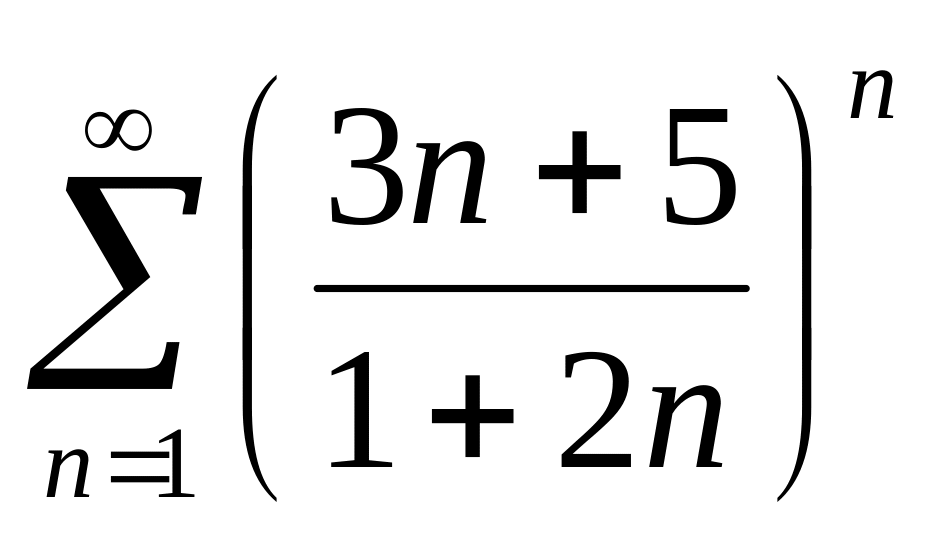 .
.Знайти статичний момент даної однорідної матеріальної дуги
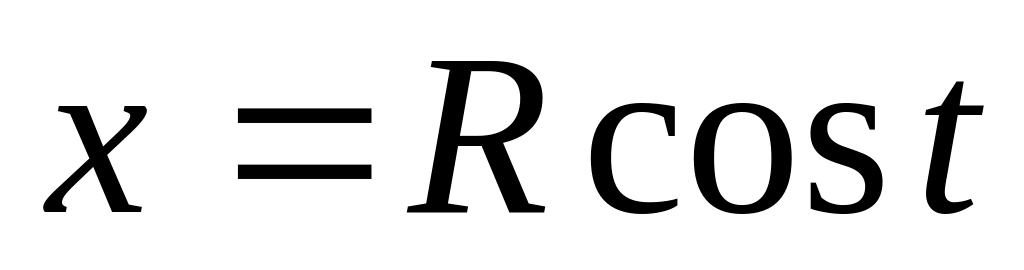 ,
,
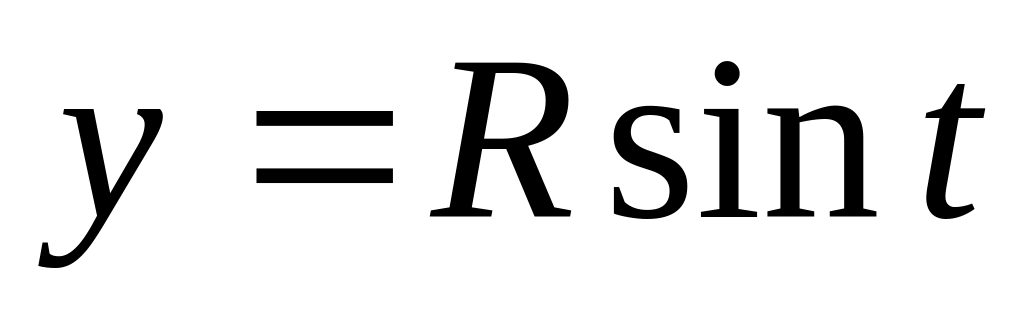 ,
,
відносно координатних віссей.
,
,
відносно координатних віссей.Знайти похідну даної функції, заданої неявно
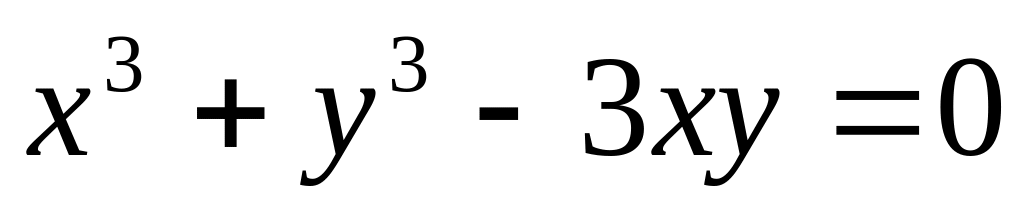 .
.Обчислити границю функції
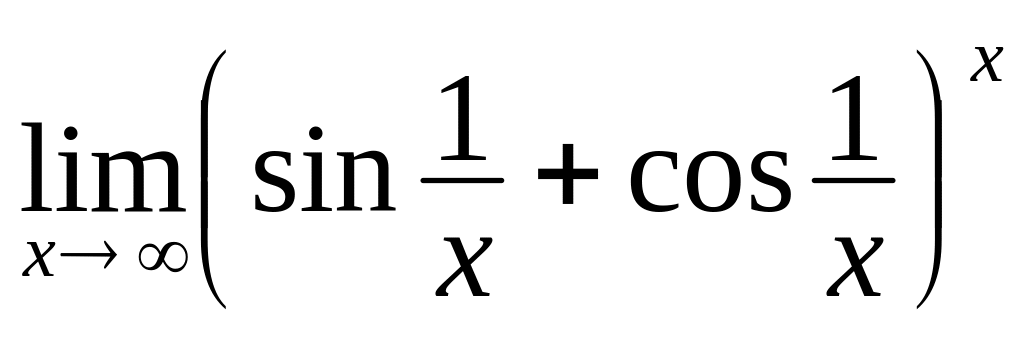 .
.Знайти даний інтеграл, скориставшись методом інтегрування частинами
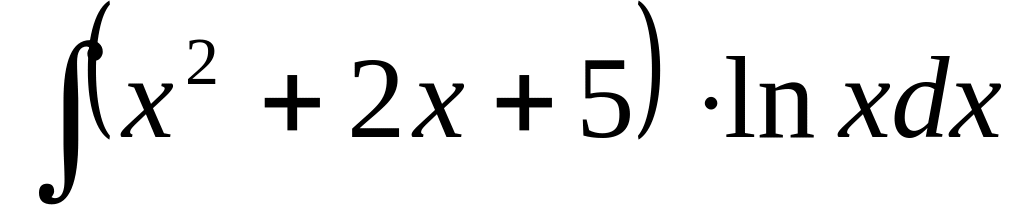 .
.Дослідити даний ряд на збіжність
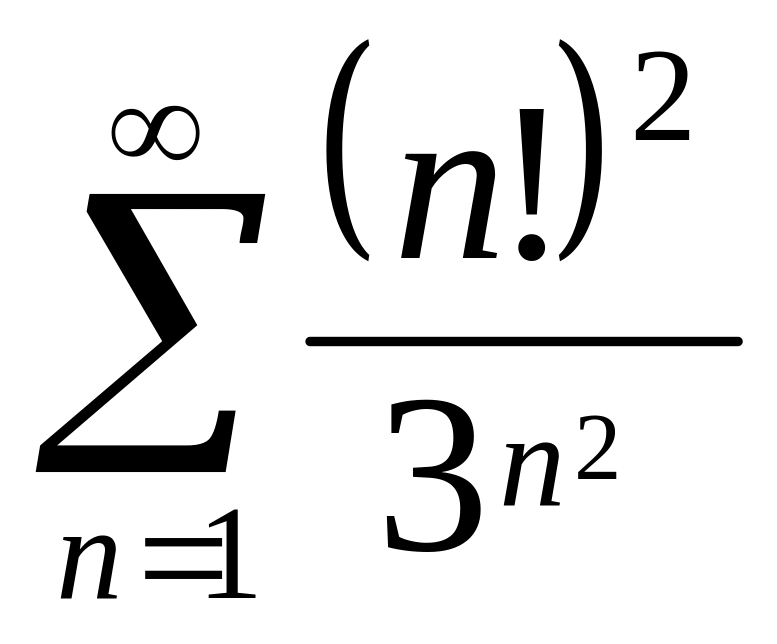 .
.Використовуя логарифмічне диференціювання, обчислити похідну даної функції
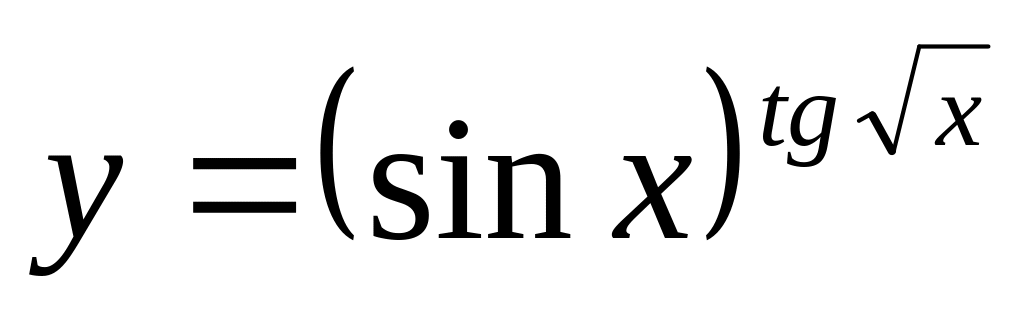 .
.Знайти інтеграл
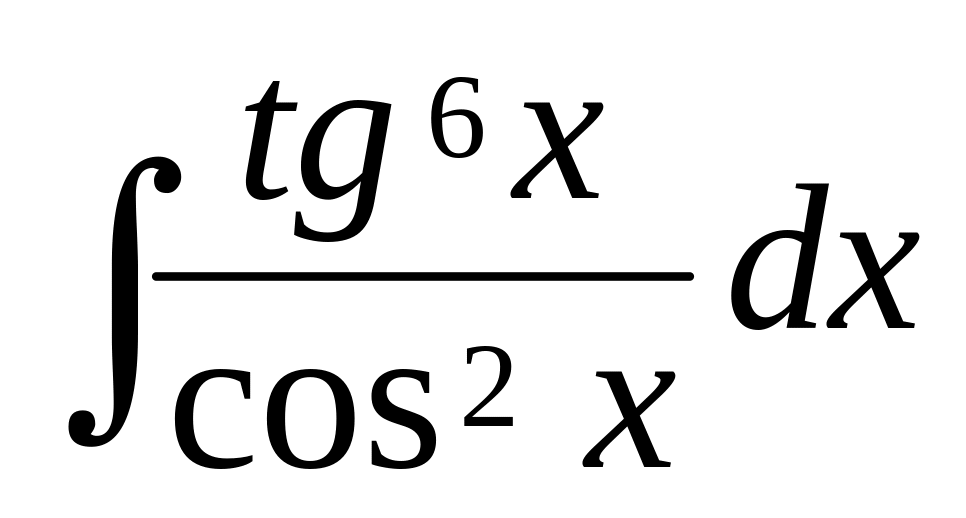 .
.Знайти область збіжності даного функціонального ряду
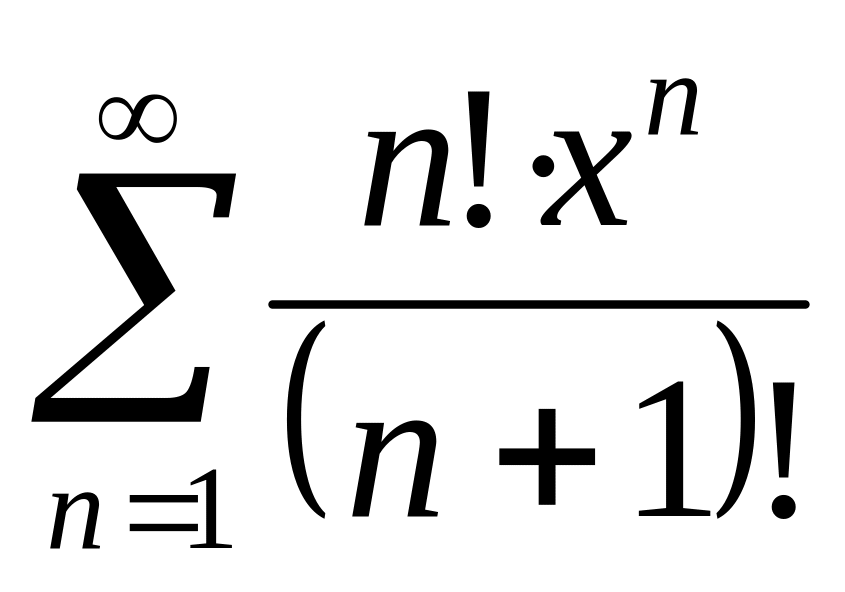 .
.Знайти довжину даної дуги кривої
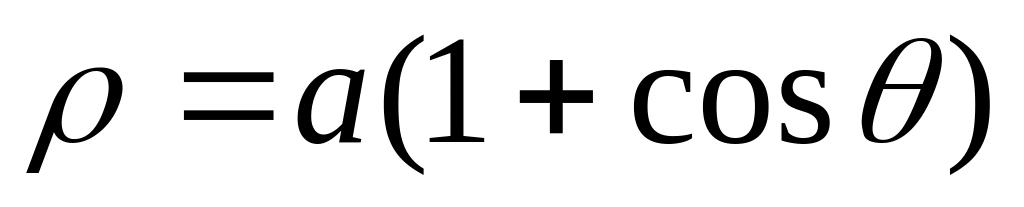 (кардіоїда).
(кардіоїда).Використовуя логарифмічне диференціювання, обчислити похідні даних функцій
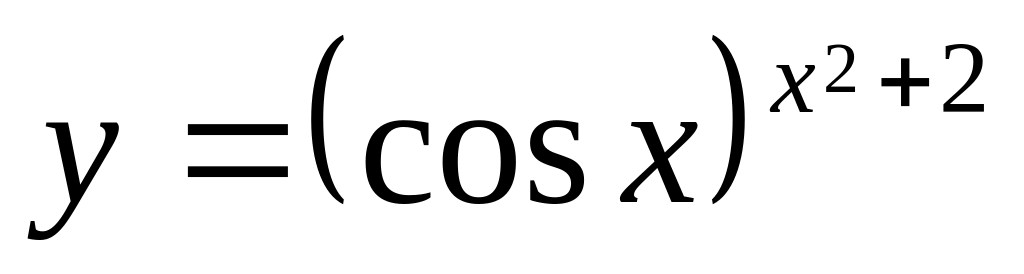 .
.Дослідити функцію на неперервність і з’ясувати характер точок розриву
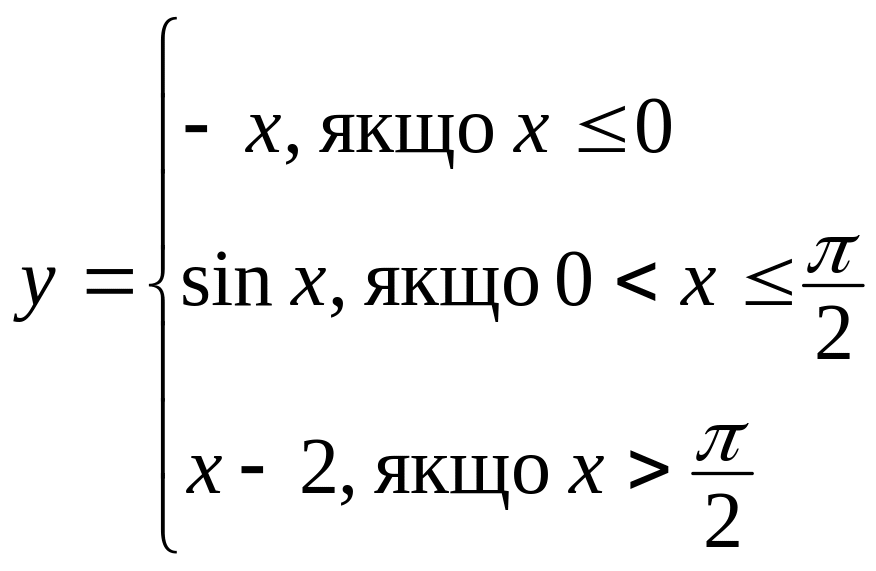 \
\Обчислити криволінійний інтеграл
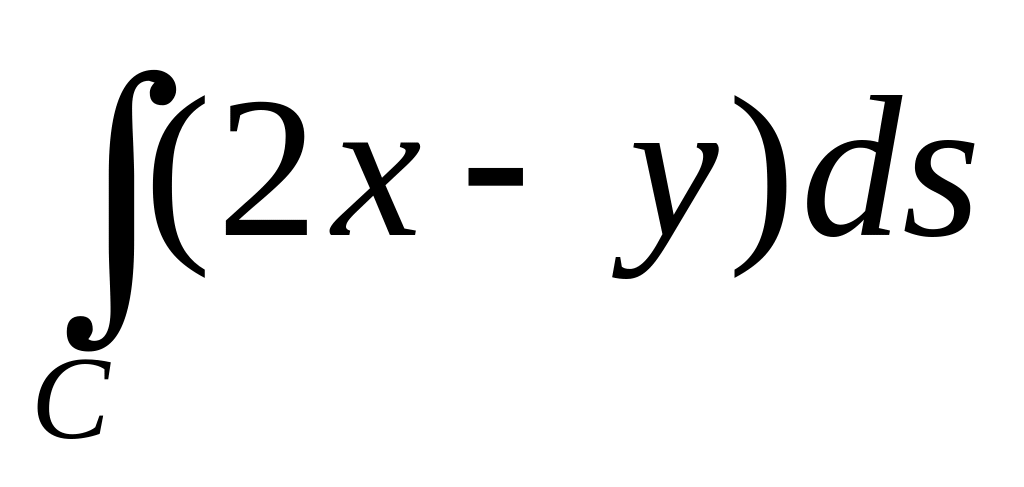 ,
де
,
де
 − відрізок прямої від точки
− відрізок прямої від точки
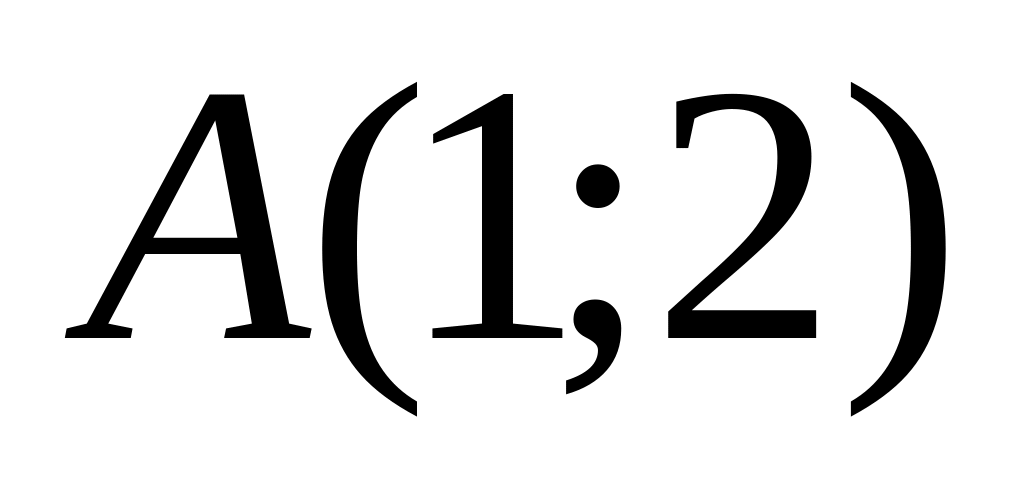 до точки
до точки
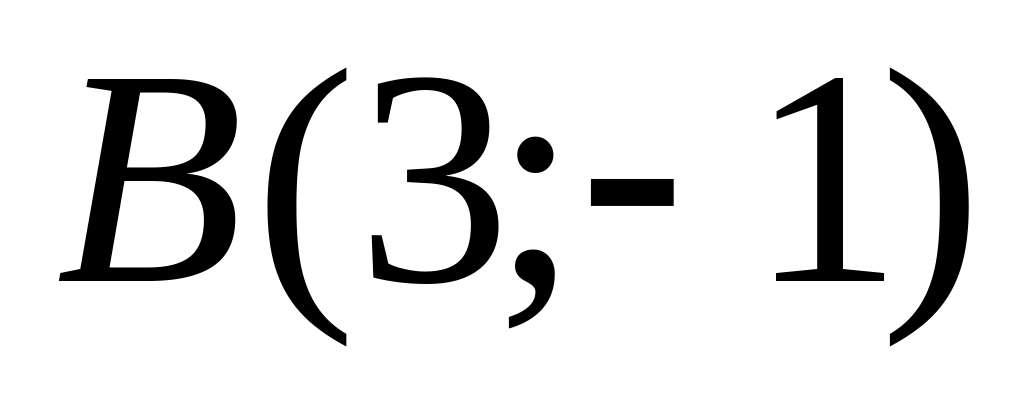 .
.Дослідити даний ряд на збіжність
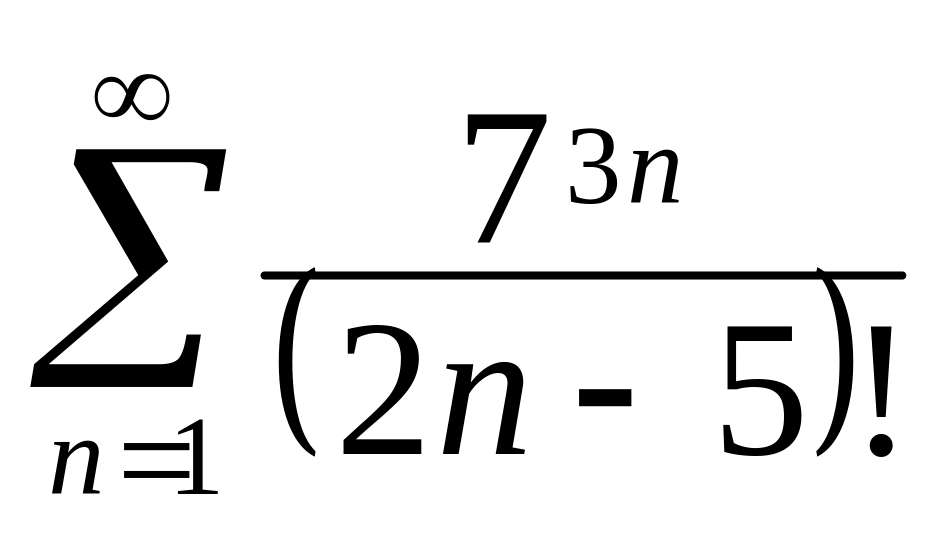 .
.Обчислити визначений інтеграл
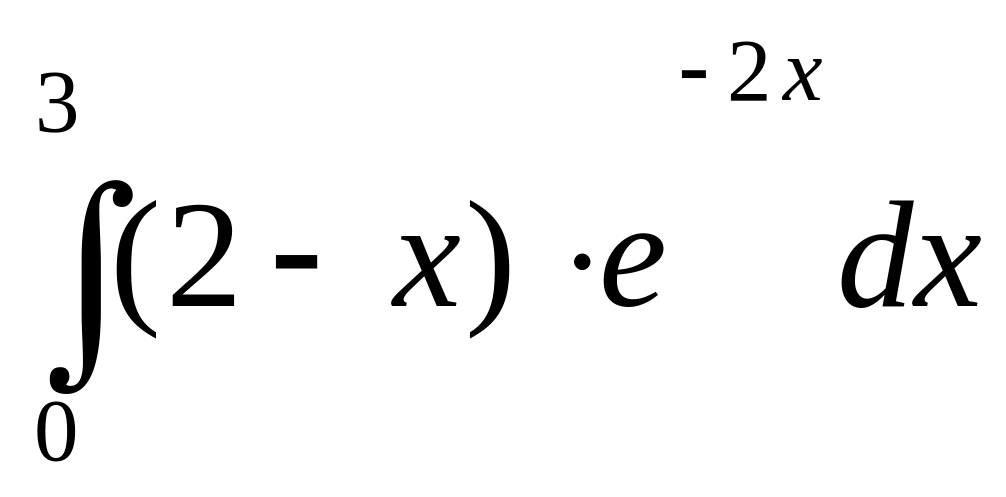
Знайти об’єм тіла, обмеженого поверхнями
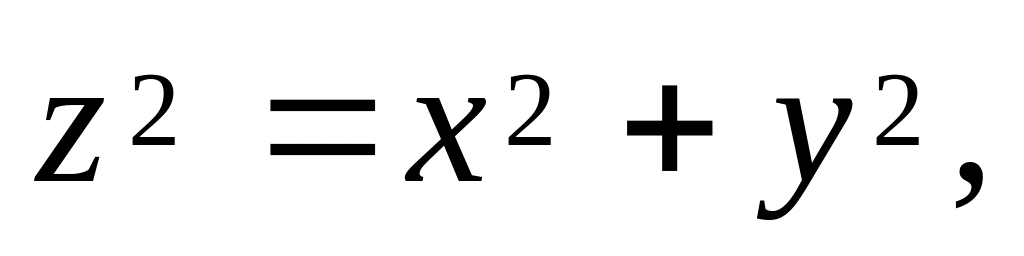
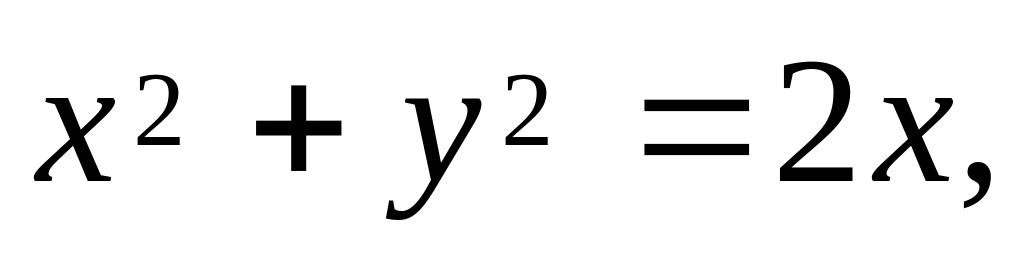
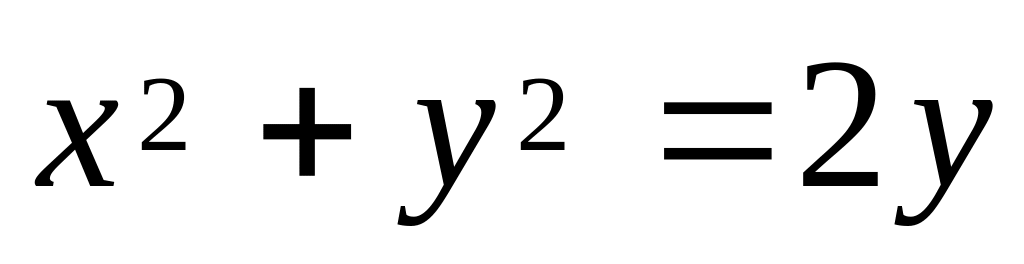 .
.Дослідити функцію на неперервність і з’ясувати характер точок розриву
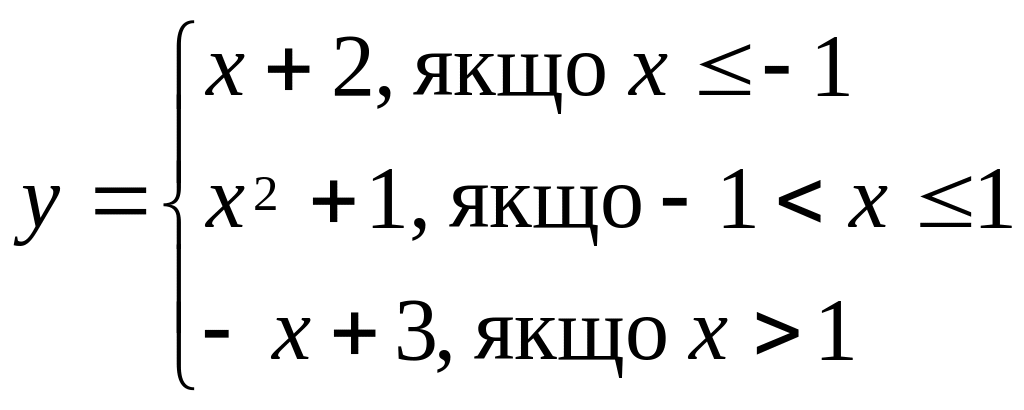
Знайти подвійний інтеграл
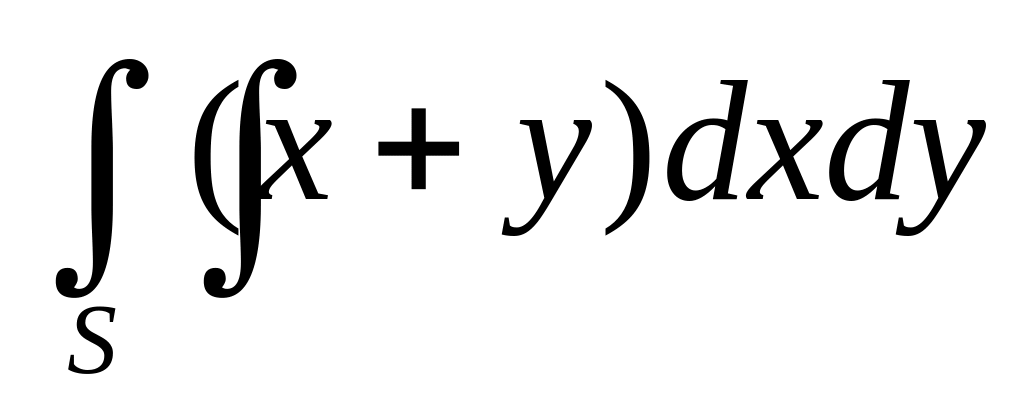 ,
якщо область
,
якщо область
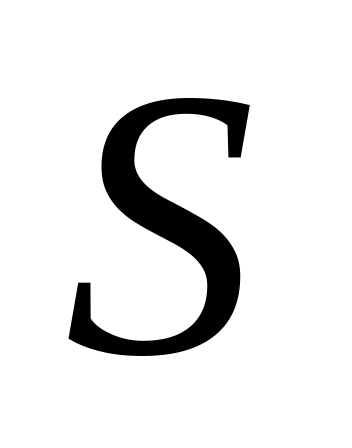 обмежена лініями
обмежена лініями
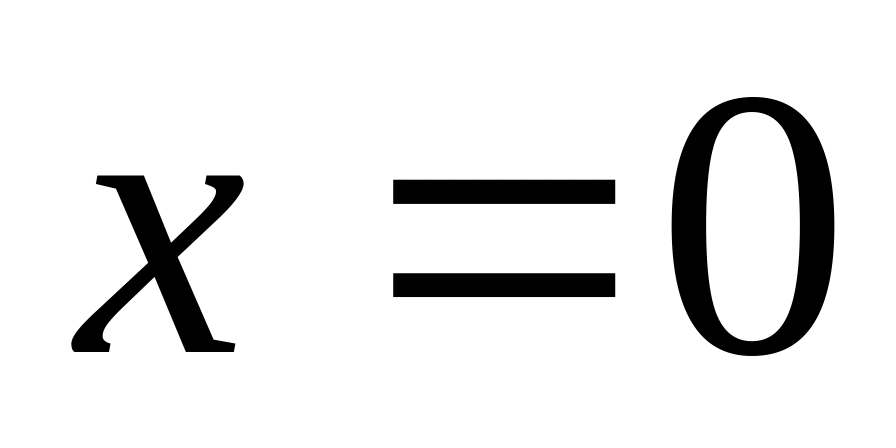 ,
,
,
,
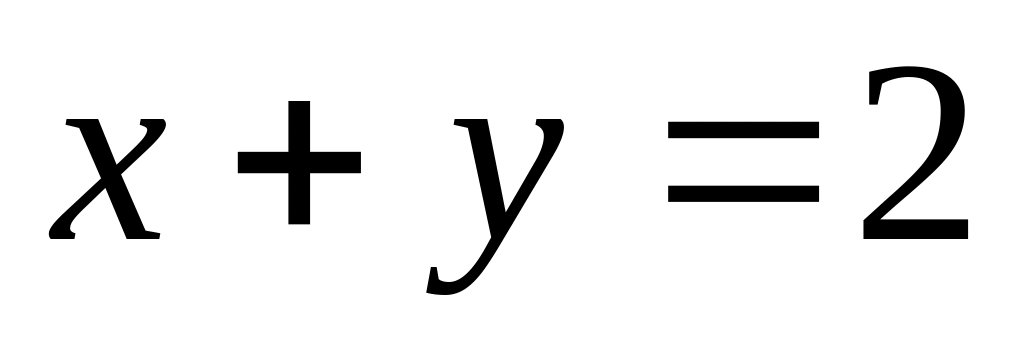 .
.Знайти границю функції, використовуючи правило Лопіталя
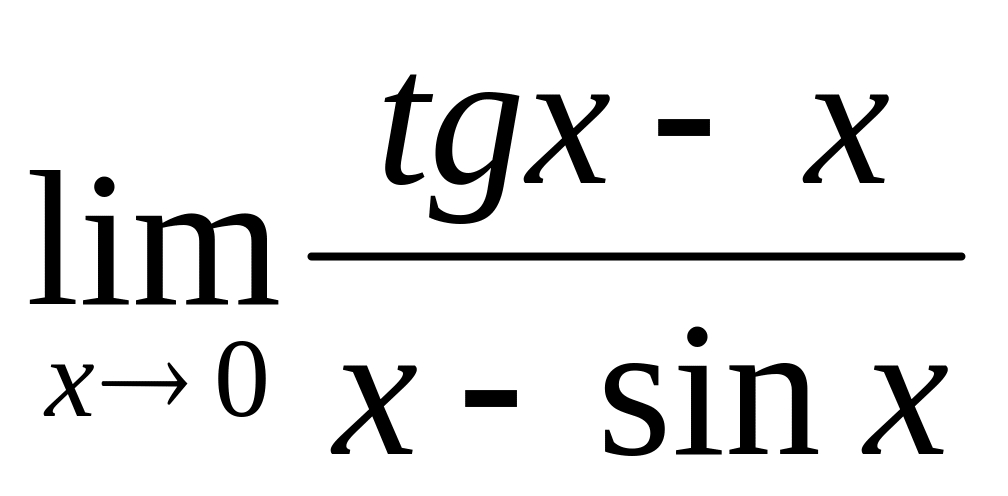 .
.За допомогою діаграм Ейлера – Венна впевнитись, що для будь – яких множин А, В і С виконується або не виконується така рівність: А|B=A|(A
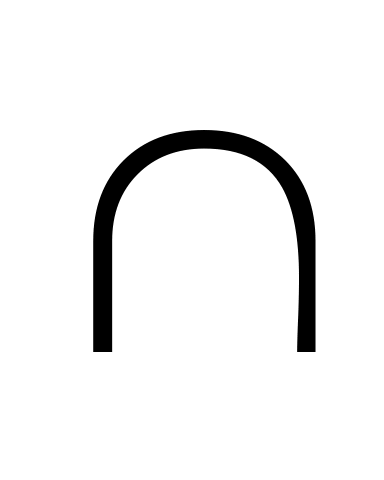 B).
B).Знайти довжину дуги кривої
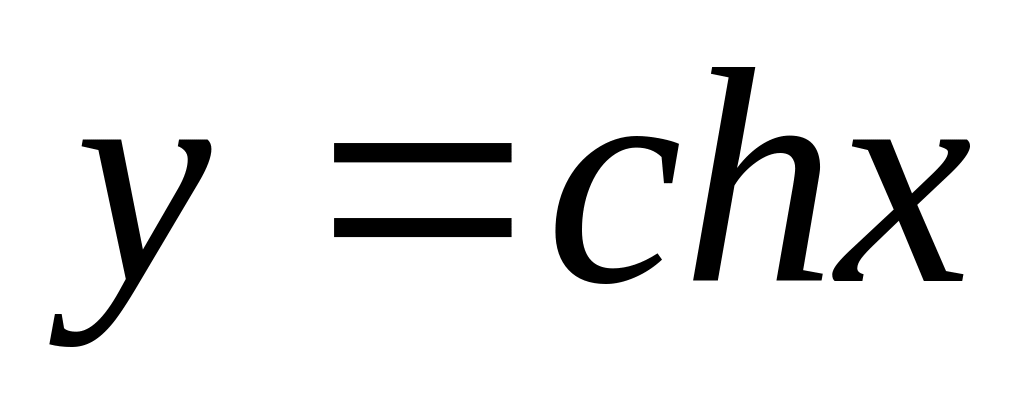 від
від
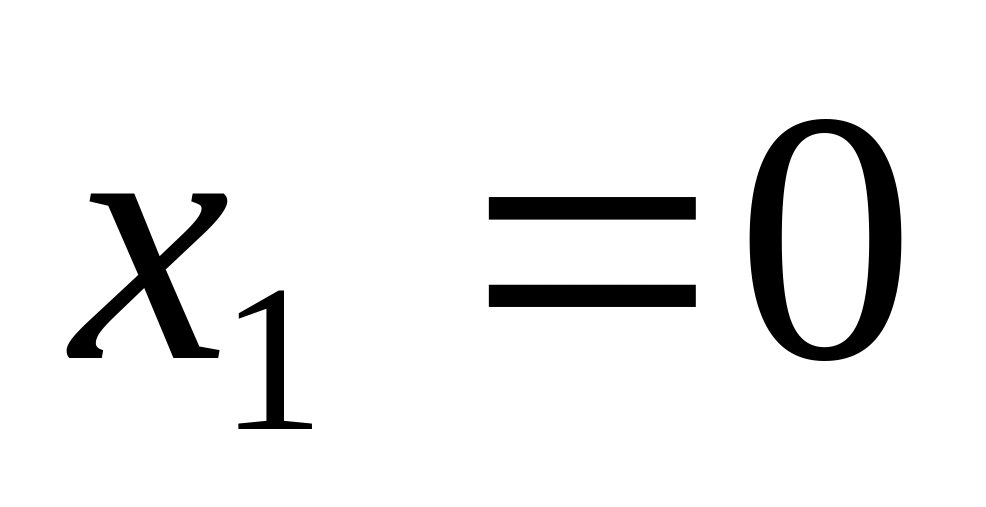 до
до
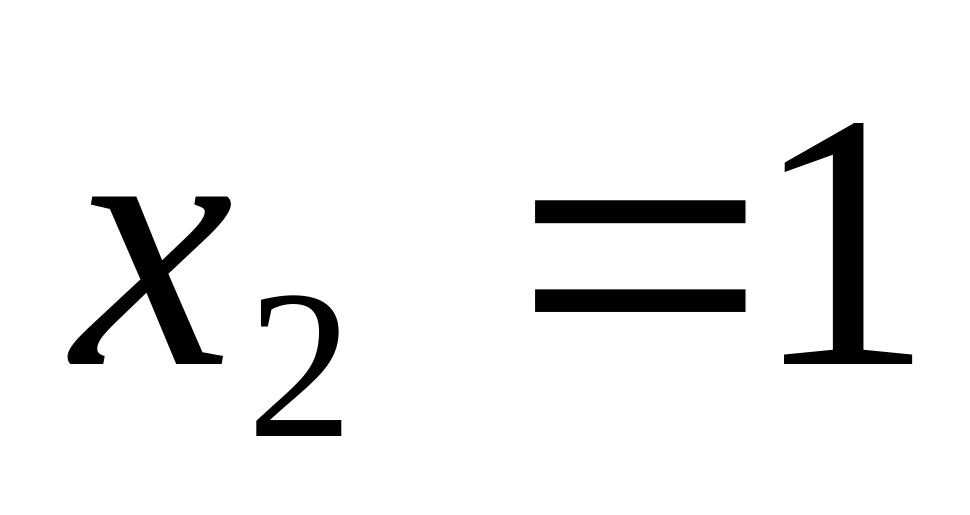 .
.
