
- •П роизведением
- •16. Неупорядоченные выборки с повторениями и без повторений. Разбиение на подмножества.
- •17.Геометрическое: Классическое определение вероятностей нельзя применять в случае бесконечного числа исходов. К описанию такой ситуации приспособлено геометрическое определение вер-ти.
- •19.Определение условной вероятности. Теоремы умножения зависимых и независимых событий.
- •38 Дискретный случайный вектор
- •Условие независимости для дискретной случайной вел-ны:
- •Условие независимости для непрерывной случайной велечины:
- •Сходимость последовательностей случайных величин
- •49. Закон больших чисел
- •55) Довер-ый интер-л для дисп-ии при неизв-ом мат-ом ожид-ии норм-о распред-ой ген-ой совоку-ти.( )
- •Квантили распред-я
38 Дискретный случайный вектор
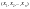 -называется
дискретным, если множество значений
каждой из его координат конечно или
счетно, т.е. любая координата является
дискретной случайной величиной.
-называется
дискретным, если множество значений
каждой из его координат конечно или
счетно, т.е. любая координата является
дискретной случайной величиной.
Рассмотрим
более подробно двумерный случайный
вектор (XY).
Пусть случайная величина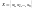 и
и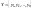
Рядом распределения случайного вектора (XY) является таблица (матрица) соответствующих значений случайных величин и их вероятностей.
X Y |
Y1 |
... |
Ym |
X1 |
P11 |
... |
P1m |
.... |
... |
... |
.... |
Xn |
Pn1 |
.... |
Pnm |

Непрерывный случайный вектор
О. Случайный вектор (XY) называется непрерывным, если случайные ф-ии распределения непрерывны и дважды дифференцируемы всюду, за исключением конечного числа конечных точек.
О.
Совместной (двумерной) вероятностью
случайного вектора (XY)
называется ф-ия: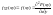
Вероятностный смысл:
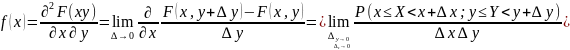
39 Свойства
1)
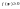 (тк
(тк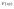 неубывающая
ф-ия)
неубывающая
ф-ия)
2)
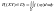 .
Док-во: разобьем область Д прямыми,
параллельными осям координат, на n
частичных областей ДК
.
Док-во: разобьем область Д прямыми,
параллельными осям координат, на n
частичных областей ДК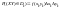 ;
;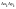 -стороны
прямоугольника Декарта.
-стороны
прямоугольника Декарта.
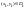 ,
т.к.
,
т.к.
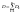 то
то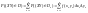 переходя
в это равенстве к
переходя
в это равенстве к
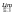 получим:
получим:
3)
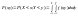
4)
условия нормировки:
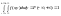
5) Свойство
согласованности:
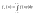 ;
;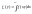
40. Пусть Х и У-произвольные, стохастически связанные(зависимые) случайные величины с совместной функцией рапределения F(X,У). Если известно, что случ. вел-на У приняла значение У=у, то закон распределения случ вел-ны Х изменится. Новый закон распределения Х наз-ся условным законом распределения, при условии,что У=у. Характеристикой условного з-на распределения является условная функция распределения:
F(х I Y=y) = P(X<x I Y=y)
Если P(Y=y)=0, то это определение не имеет смысла.
Рассмотрим дискрет. случ. вектор (Х,У):
Пусть
случ. вел-ны Х и У принимают значения
(х1,х2,…,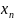 ),
(у1,у2,…,
),
(у1,у2,…,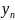 )
соответсвенно, тогда:
)
соответсвенно, тогда:
F(х
I Y=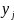 )
= P(X<x I Y=
)=
)
= P(X<x I Y=
)=
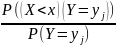 =
=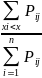
Аналогично:
F(y
I
X=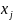 )
=
)
=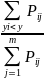
Рассмотрим непр случ вектор:
Условная функция распределения в этом случае опред след образом:
F(х
I
Y=y)
= P(X<x
I
Y=y)
=
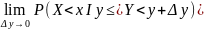 =
=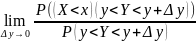 =
=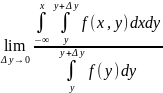 =
[применим теор о среднем где
=
[применим теор о среднем где
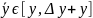 ]=
]=
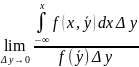 =
[при
=
[при
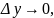
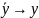 ]
=
]
=
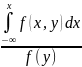
41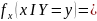
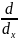 F(x
I Y=y) =
F(x
I Y=y) =
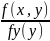
Аналогично:
F(y
I
X=x)
=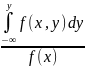
fy(y
I X=x) =
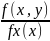
Из этих формул выразим совместную плотность вероят.:
f(x,y) = fy(y)fx(x I Y=y) = fx(x)fy(y I X=x) – формула произведения плотностей вероятностей.
Проинтегрируем равенство f(x,y) = fy(y)fx(x I Y=y) по у:
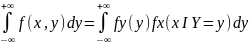
Аналогично:
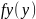 =
=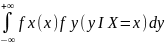
Эти 2 формулы наз-ся формулами полной вероятности. Они позволяют находить маргинальную плотность 1ой случ величины по известной маргинальной плотности другой и условной плотности.
Запишем формулу Бейеса:
fx(x
I
Y=y)
=
=
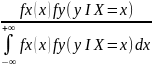
Аналогично:
fy(y
I
X=x)
=
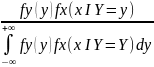
42.Две случайные величины Х и У называются независимыми, если независимы связанные с ними события ( Х=х,У=у и т.п.)
Т.к. свойство независимости соб. взаимное, то и свойство независимости случайных величин также взаимно,т.е. если Х не зависит от У то и У не зависит от Х и наоборот.
В терм. з-нов распределения условие независимости имеет вид:
F(x,y) = P((X<x)*(Y<y)) = P(X<x)*P(Y<y) = F(x)F(y), т.е. для независ. случ. величины совместная функция распределения равна произведению функций распределений отдельного компонента вектора.
