Міністерство освіти і науки України

Сумський Державний Університет

Кафедра комп’ютерних наук

Курсова робота з дисципліни «Чисельні методи» на тему:

«Чисельні методи визначення кратних інтегралів»

Виконала ст. гр. Ін-91

Пальчех М. В.

Перевірила викладач к.к.н.

Назаренко Л. Д.

Суми 2011

План

1. Інформаційний огляд теми

2. Викладення методу

3. Реалізація методу на прикладі

   • Програмна реалізація

   • Пакетна реалізація

4. Висновки і результати

5. Список використаних джерел

1. Інформаційний огляд теми

У великій кількості наук, таких як фізика, хімія, математика, економіка, оптимізація, теорія управління та ін. існує безліч задач, які пов’язані з чисельним інтегруванням. Чисельне інтегрування застосовується тоді, коли:

• Сама підінтегральна функція не задана аналітично. Наприклад, вона представлена ​​у вигляді таблиці (масиву) значень у вузлах деякої розрахункової сітки.

• Аналітичне подання підінтегральної функції відомо, але її первісна не виражається через аналітичні функції. Наприклад, .

До задач, які вирішує інтегрування, відносяться, як правило, задачі на знаходження площі, маси, щільності, об’єму, задачі, що пов’язані з простором великої розмірності (у теорії струн) , а також задачах, де є системи з багатьма степенями свободи.

Чисельне інтегрування – обчислення значення (як правило наближеного) визначеного інтеграла, засноване на тому, що величина інтеграла чисельно дорівнює площі криволінійної трапеції.

Задача полягає в заміні підінтегральної функції , для котрої важко або неможливо записати первісну у аналітиці, деякою апроксимуючою функцією Такою функцією зазвичай є кусочний поліном . Тобто , де - апріорна похибка методу на інтервалі інтегрування, а - апріорна похибка методу на окремому кроці інтегрування.

Кратний інтеграл або ж багатократний інтеграл степеня n, це визначений інтеграл по n змінних з функції n змінних:

.

Існує велика кількість методів чисельного обчислення кратних інтегралів. Ці методи називають кубатурними. Їх можна поділити на декілька груп:

• Методи Н’ютона-Котеса.

Тут - поліном різних степенів. До цієї групи відносять також метод Сімпсона, метод сіток.

• Методи статичних випробувань (Методи Монте-Карло).

Вузли сітки для кубатурного інтегрування вибираються за допомогою датчика випадкових чисел, відповідь носить імовірнісний характер. В основному застосовуються для обчислення кратних інтегралів. Цей метод дуже доречно використовувати при кратності інтеграла >3.

• Сплайнові методи.

Тут - кусковий поліном з умовами зв'язку між окремими поліномами за допомогою системи коефіцієнтів.

• Методи найвищої алгебраїчної точності.

Ці методи забезпечують оптимальну розстановку вузлів сітки інтегрування і вибір вагових коефіцієнтів в задачі . Сюди відноситься метод Гауса-Крістофеля (обчислення невласних інтегралів) і метод Маркова.

Мене дуже зацікавив метод чисельного інтегрування Монте-Карло тим, що за допомогою нього можна вирішити дуже складні задачі, пов’язані з інтегруванням функцій великої розмірності, задачі, які дуже складно вирішити іншими методами, так як їх використання не є доцільним із-за швидкого росту зростання числа точок сітки та/або складної границі інтегрування.

2. Викладення методу

Для того, щоб зрозуміти суть методу, потрібно розібратися в понятті математичного сподівання.

Математичне сподівання – міра середнього значення випадкової величини в теорії ймовірностей. Позначається як .

Метод Монте-Карло для обчислення інтегралів заклечається в генеруванні випадкових точок та усереднюванні значення функції в них.

Припустимо, потрібно обчислити визначений інтеграл 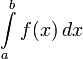. Розглянемо випадкову величину , рівномірно розподілену на відрізку інтегрування . Тоді так само буде випадковою величиною, причому її математичне сподівання виражається як 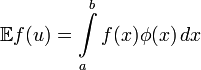, де - щільність розподілу випадкової величини , що дорівнює на ділянці .

Таким чином, шуканий інтеграл виражається як .

Але математичне очікування випадкової величини можна легко оцінити, змоделювавши цю випадкову величину і порахувавши вибіркове середнє.

Отже, кидаємо точок, рівномірно розподілених на , для кожної точки обчислюємо . Потім обчислюємо вибіркове середнє: .

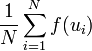У підсумку отримуємо оцінку інтеграла: .

Точність оцінки не залежить від вигляду підінтегральної функції чи від кратності інтегралу. Вона залежить тільки від кількості точок . Похибку методу розраховують за формулою Цю похибку можна зменшити, якщо збільшити кількість випробувань n або застосовуючи додатково деякі методи з теорії ймовірностей(методи істотної вибірки або випадкового

блукання).

Двукратні інтеграли будуть обчислюватись по формулі .

Інтеграли, кратність яких більше 2, будуть обчислюватись аналогічно.