matan_test_ekz2

Вопрос: Определите частное решение дифференциального уравнения , удовлетворяющее начальным условиям:

Ответ:

Вопрос: Определите частное решение дифференциального уравнения удовлетворяющее начальным условиям: .

Ответ:

Вопрос: Общим решением дифференциального уравнения является функция

Ответ:

Вопрос: Уравнение Бернулли

Ответ:

Вопрос: Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям

Ответ:

Вопрос: Если и - два линейно независимых решения дифференциального уравнения , то общее решение этого уравнения будет

Ответ:

Вопрос: Определите частное решение дифференциального уравнения 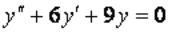, удовлетворяющее начальным условиям: .

Ответ:

Вопрос: Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям

Ответ:

Вопрос: Однородное уравнение.

Ответ:

Вопрос: Уравнения в полных дифференциалах.

Ответ:

Вопрос: Уравнение с разделяющимися переменными.

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения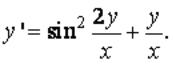

Ответ:

Вопрос: Определите частное решение дифференциального уравнения , удовлетворяющее начальным условиям:

Ответ:

Вопрос: Линейное уравнение.

Ответ:

Вопрос: Определите частное решение дифференциального уравнения , удовлетворяющее начальным условиям:

Ответ:

Вопрос: Характеристическое уравнение неоднородного линейного уравнения имеет корни и . Число равно хотя бы одному корню характеристического уравнения. Укажите вид его частного решения.

Ответ: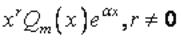

Вопрос: Уравнение с разделяющимися переменными.

Ответ:

Вопрос: Укажите вид частного решения для неоднородного линейного уравнения со специальной правой частью:

Ответ: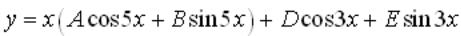

Вопрос: Определите частное решение дифференциального уравнения , удовлетворяющее начальным условиям:

Ответ:

Вопрос: Дифференциальное уравнение называется Ответ: линейным неоднородным

Вопрос: Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям

Ответ: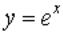

Вопрос: Линейное уравнение.

Ответ:

Вопрос: Укажите вид частного решения для неоднородного линейного уравнения со специальной правой частью:

Ответ:

Вопрос: Указать вид частного решения для уравнения со специальной правой частью.

Ответ:

Вопрос: Определите частное решение дифференциального уравнения , удовлетворяющее начальным условиям:

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения .

Ответ:

Вопрос: Если дифференциальное уравнение имеет два частных решения и , то

Ответ: будет, и будет решением Вопрос: Метод вариации произвольного постоянного.

Ответ:

Вопрос: Уравнение Бернулли

Ответ:

Вопрос: Определите частное решение дифференциального уравнения удовлетворяющее начальным условиям:

Ответ:

Вопрос: Уравнение Бернулли

Ответ:

Вопрос: Метод вариации произвольного постоянного.

Ответ:

Вопрос: С помощью метода вариации произвольного постоянного определите общее решение дифференциального уравнения

Ответ:

Вопрос: Однородное уравнение.

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения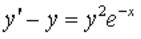

Ответ: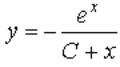

Вопрос: Указать вид частного решения для уравнения со специальной правой частью.

Ответ: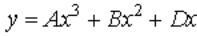

Вопрос: Найдите общее решение неоднородного линейного уравнения со специальной правой частью:

Ответ:

Вопрос: Линейное уравнение.

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения .

Ответ: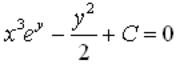

Вопрос: С помощью метода вариации произвольного постоянного определите общее решение дифференциального уравнения

Ответ:

Вопрос: Дифференциальное уравнение допускает понижение порядка путем подстановки:

Ответ:

Вопрос: Характеристическое уравнение неоднородного линейного уравнения имеет корни и . Если число равно одному из корней или 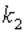, то частное решение имеет вид:

Ответ: 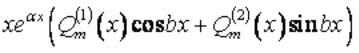, где

Вопрос: Линейное уравнение.

Ответ:

Вопрос: Укажите вид частного решения для неоднородного линейного уравнения со специальной правой частью :

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения .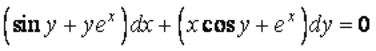

Ответ:

Вопрос:

Ответ:

Вопрос: Укажите вид частного решения для неоднородного линейного уравнения со специальной правой частью:

Ответ:

Вопрос:

Ответ:

Вопрос: Указать вид частного решения для уравнения со специальной правой частью.

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения

Ответ:

Вопрос: Определите частное решение дифференциального уравнения , удовлетворяющее начальным условиям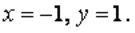

Ответ:

Вопрос: Найти частное решение дифференциального уравнения, удовлетворяющее заданному начальному условию.

Ответ:

Вопрос: Решение линейного однородного уравнения с постоянными коэффициентами 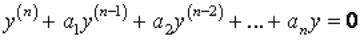ищется в виде:

Ответ: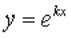

Вопрос: Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям

Ответ:

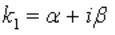Вопрос: Характеристическое уравнение дифференциального уравнения имеет комплексные корни и . Тогда общее решение дифференциального уравнения будет:

Ответ:

Вопрос: Определите частное решение дифференциального уравнения , удовлетворяющее начальным условиям:

Ответ:

Вопрос: Метод вариации произвольного постоянного.

Ответ:

Вопрос: Найдите общее решение неоднородного линейного уравнения со специальной правой частью: .

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения .

Ответ:

Вопрос: Определите частное решение дифференциального уравнения , удовлетворяющее начальным условиям:

Ответ:

Вопрос: Дифференциальное уравнение I-го порядка называется линейным, если

Ответ: оно имеет вид Вопрос: Уравнение Бернулли

Ответ:

Вопрос: Уравнения в полных дифференциалах.

Ответ:

Вопрос: Уравнение с разделяющимися переменными.

Ответ:

Вопрос: Определите частное решение дифференциального уравнения , удовлетворяющее начальным условиям:

Ответ:

Вопрос: Линейное уравнение первого порядка решается путем подстановки:

Ответ:

Вопрос: Метод вариации произвольного постоянного.

Ответ:

Вопрос: С помощью метода вариации произвольного постоянного определите общее решение дифференциального уравнения

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения .

Ответ:

Вопрос: Уравнения в полных дифференциалах.

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения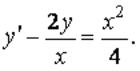

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения

Ответ:

Вопрос: Дифференциальное уравнение допускает понижение порядка путем подстановки:

Ответ: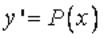

Вопрос: Найдите общее решение дифференциального уравнения .

Ответ:

Вопрос: Метод вариации произвольного постоянного.

Ответ:

Вопрос: Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям

Ответ:

Вопрос: Для того, чтобы дифференциальное уравнение представляло собой уравнение в полных дифференциалах, необходимо, чтобы было выполнено условие:

Ответ:

Вопрос: Найти частное решение дифференциального уравнения, удовлетворяющее заданному начальному условию.

Ответ:

Вопрос: Уравнение Бернулли решается путем подстановки:

Ответ:

Вопрос: Найти частное решение дифференциального уравнения, удовлетворяющее заданному начальному условию.

Ответ:

Вопрос: Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.

Ответ:

Вопрос: Уравнение с разделяющимися переменными.

Ответ:

Вопрос: Функция называется однородной функцией n-го измерения, если справедливо тождество:

Ответ:

Вопрос: Какое из дифференциальных уравнений является уравнением с разделяющимися переменными:

Ответ: а), б) и с)

Вопрос: Найдите общее решение дифференциального уравнения .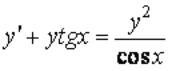

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения .

Ответ:

Вопрос: Однородное уравнение.

Ответ:

Вопрос: Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.

Ответ:

Вопрос: Укажите вид частного решения для неоднородного линейного уравнения со специальной правой частью:

Ответ: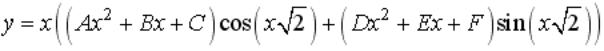

Вопрос: Укажите вид частного решения для неоднородного линейного уравнения со специальной правой частью:

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения .

Ответ:

Вопрос: Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям

Ответ:

Вопрос: Определите частное решение дифференциального уравнения , удовлетворяющее начальным условиям: .

Ответ:

Вопрос: Дифференциальное уравнение называется однородным относительно , если функция является Ответ: однородной функцией нулевого измерения

Вопрос: Линейное однородное уравнение с постоянными коэффициентами имеет характеристическое уравнение вида:

Ответ:

Вопрос: Укажите вид частного решения для неоднородного линейного уравнения со специальной правой частью:

Ответ:

Вопрос:

Ответ:

Вопрос: Метод вариации произвольного постоянного.

Ответ:

Вопрос: Порядком дифференциального уравнения называется: Ответ: наивысший порядок производных уравнения

Вопрос: Указать вид частного решения для уравнения со специальной правой частью.

Ответ:

Вопрос: Найти частное решение дифференциального уравнения, удовлетворяющее заданному начальному условию.

Ответ:

Вопрос: Уравнения в полных дифференциалах.

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения .

Ответ:

Вопрос: Однородное дифференциальное уравнение порядка решается путем подстановки:

Ответ:

Вопрос: Указать вид частного решения для уравнения со специальной правой частью.

Ответ:

Вопрос: Определите частное решение дифференциального уравнения , удовлетворяющее начальным условиям:

Ответ:

Вопрос: Если дифференциальное уравнение имеет какое-либо частное решение , а соответствующее однородное уравнение имеет общее решение , то общее решение неоднородного уравнения будет:

Ответ: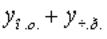

Вопрос: Найдите общее решение дифференциального уравнения .

Ответ:

Вопрос:

Ответ:

Вопрос: Указать вид частного решения для уравнения со специальной правой частью.

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения .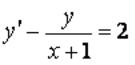

Ответ:

Вопрос: Характеристическое уравнение неоднородного линейного уравнения имеет корни и не равные . Укажите вид его частного решения.

Ответ:

Вопрос: С помощью метода вариации произвольного постоянного определите общее решение дифференциального уравнения:

Ответ:

Вопрос: Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям

Ответ:

Вопрос: Однородное уравнение.

Ответ:

Вопрос: Определите частное решение дифференциального уравнения , удовлетворяющее начальным условиям:

Ответ:

Вопрос: Определите частное решение дифференциального уравнения , удовлетворяющее начальным условиям:

Ответ:

Вопрос: Указать вид частного решения для уравнения со специальной правой частью.

Ответ:

Вопрос: Определите частное решение дифференциального уравнения , удовлетворяющее начальным условиям: .

Ответ:

Вопрос: С помощью метода вариации произвольного постоянного определите общее решение дифференциального уравнения

Ответ:

Вопрос: Найдите общее решение дифференциального уравнения .

Ответ:

Вопрос: Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям

Ответ:
Вопрос: Определите частное решение дифференциального уравнения		, удовлетворяющее начальным условиям:
Ответ:
Вопрос: Определите частное решение дифференциального уравнения		, удовлетворяющее начальным условиям:
Ответ:
Вопрос: Характеристическое уравнение неоднородного линейного уравнения		имеет корни	и . Если число	не равно ни одному из корней или, то частное решение имеет вид:
Ответ:	, где

Вопрос: Найдите общее решение дифференциального уравнения

Ответ:

Вопрос: Характеристическое уравнение дифференциального уравнения имеет два одинаковых корня . Тогда общее решение дифференциального уравнения будет:

Ответ: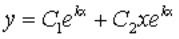

Вопрос: Дифференциальное уравнение называется Ответ: линейным однородным n-го порядка

Вопрос: С помощью метода вариации произвольного постоянного определите общее решение дифференциального уравнения

Ответ: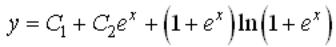

Вопрос: Уравнение Бернулли имеет вид:

Ответ:

Вопрос: Укажите вид частного решения для неоднородного линейного уравнения со специальной правой частью:

Ответ:

copyright jet post2.1