
Билеты Егоров
.docxОглавление
1.Понятие двойного интеграла 3
2.Основные свойства двойного интеграла 6
3.Вычисление двойного интеграла через двукратный 6
4.Основные свойства двукратного интеграла 7
5.Вычисление площади и объёма с помощью двукратного 10
6.Двойной интеграл в полярных координатах 12
7.Вычисление площади поверхности с помощью двукратного 15
8.Понятие тройного интеграла 18
9.Вычисление тройного через трёхкратный 20
10.Вычисление объёма тела с помощью тройного интеграла 23
11) Физические приложения двойного интеграла 25
12) Физические приложения тройного интеграла 26
13) Понятие криволинейного интеграла 27
14) Основные свойства криволинейного интеграла 29
16) Выражение площади области, ограниченной кривой, через криволинейный интеграл 31
17) Задача о вычислении работы на некотором криволинейном пути 33
20) Элементы теории поля (векторное, скалярное, градиент, дивергент, оператор Гамильтона, оператор Лапласса) 37
21) Числовые ряды, операции с ними 39
22) Необходимый признак сходимости ряда 41
23) Признак Даламбера 42
24) Признак Коши (Радикальный) 44
25) Признак Коши (интегральный) 44
26) Признак сравнения первого рода 45
27) Знакочередующиеся ряды. Теорема Лейбница 46
28) Знакопеременные числовые ряды. Достаточное условие сходимости числового ряда 48
29) Абсолютная и условная сходимости знакопеременных рядов 49
30) Функциональные ряды 49
31) Мажорируемые ряды 51
32) Интегрирование и дифференцирование рядов 52
33) Степенные ряды. Теорема Абеля 53
34) Интервал сходимости степенного ряда 55
35) Ряды Тейлора и Маклорена 56
36) Разложение основных элементарных функций в ряды Тейлора и Маклорена 56
37) Приложение степенных рядов. Биноминальный ряд 57
38) Применение степенных рядов. Вычисление определённых интегралов и логарифмов 58
39) Применение теории полей для решения диффур. Метод итераций 59
40) Применение теории полей для решения диффур. Метод последовательного дифференцирования 61
40) 62
41) Применение теории полей для решения диффур. Способ неопределенных коэффициентов 64
42) Ряды Фурье. (основные определения, постановка задач) 64
43) Пример разложения функции в ряд Фурье 66
44) Ряды Фурье для чётных и нечётных функций 67
45) Ряды Фурье для функций с периодом 2l 70
-
Понятие двойного интеграла

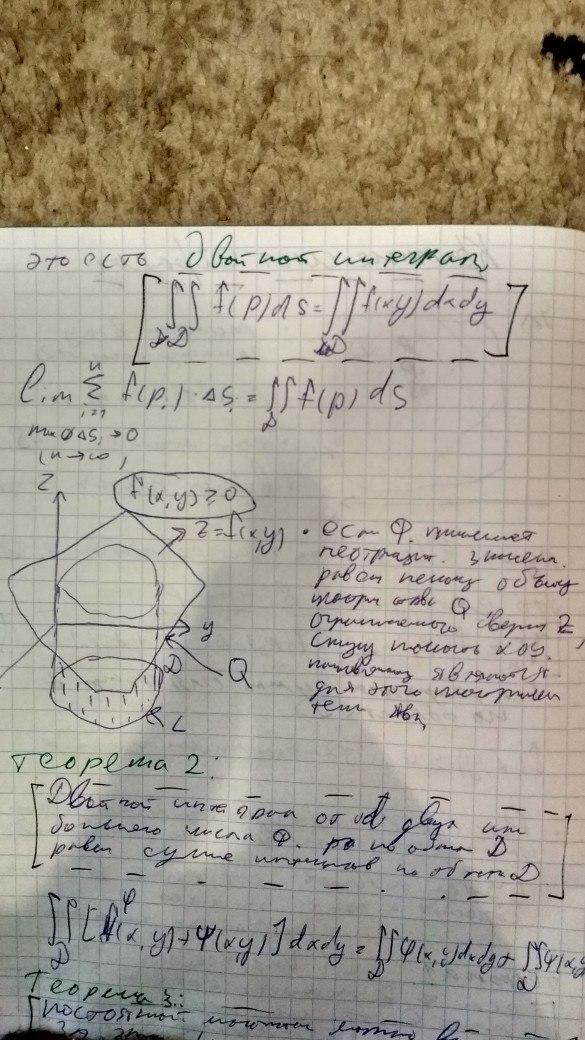
-
Основные свойства двойного интеграла

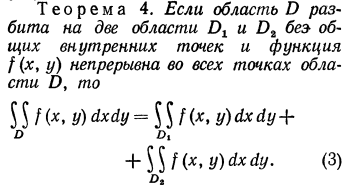
-
Вычисление двойного интеграла через двукратный


-
Основные свойства двукратного интеграла


-
Вычисление площади и объёма с помощью двукратного





-
Двойной интеграл в полярных координатах


-
Вычисление площади поверхности с помощью двукратного


-
Понятие тройного интеграла

-
Вычисление тройного через трёхкратный


-
Вычисление объёма тела с помощью тройного интеграла



11) Физические приложения двойного интеграла

12) Физические приложения тройного интеграла


13) Понятие криволинейного интеграла
Определённый интеграл – частный случай криволинейного
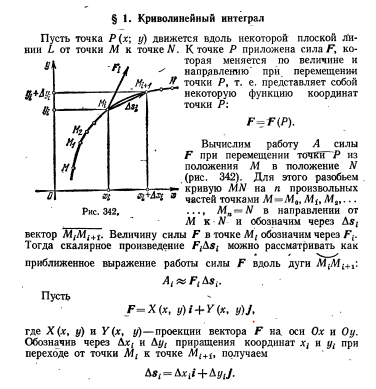

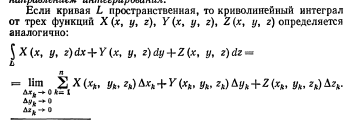
14) Основные свойства криволинейного интеграла

15) Вычисление криволинейного интеграла
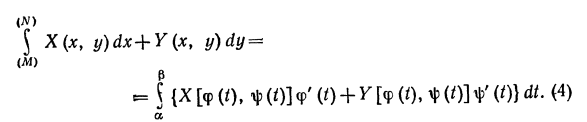


16) Выражение площади области, ограниченной кривой, через криволинейный интеграл

 17
17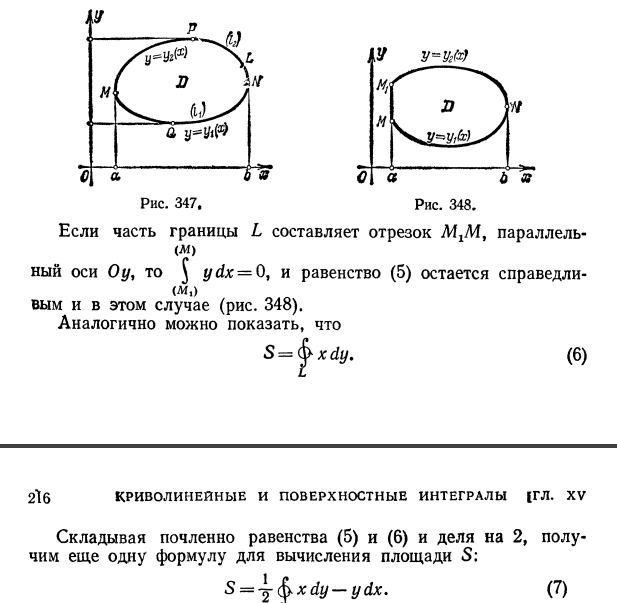
17) Задача о вычислении работы на некотором криволинейном пути

18) Формула Грина
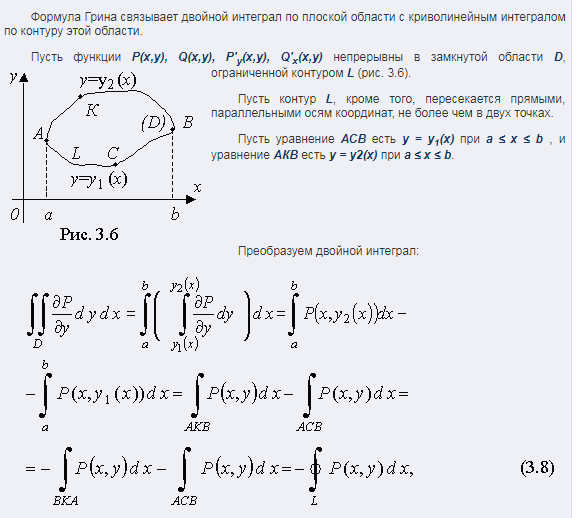

19) Условие независимости криволинейного интеграла от пути интегрирования


Криволинейный интеграл по замкнутому контуру не равняется нулю, если он выражает площадь , ограниченную рассматриваемым контуром
20) Элементы теории поля (векторное, скалярное, градиент, дивергент, оператор Гамильтона, оператор Лапласса)
Скалярное
поле определяется скалярной функцией
точки ![]() где
где ![]() -
точка пространства,
-
точка пространства, ![]() -
ее радиус-вектор.
-
ее радиус-вектор.
Скалярное поле – плоская или пространственная область, с каждой точкой которой связано определенное значение некоторой скалярной физической величины
Векторное поле - плоская или пространственная область, с каждой точкой которой связано определенное значение некоторой векторной функции.

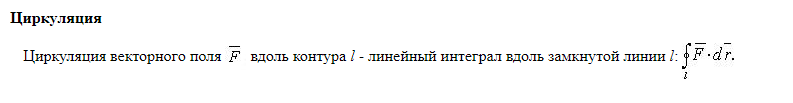





21) Числовые ряды, операции с ними






22) Необходимый признак сходимости ряда
![]()

23) Признак Даламбера

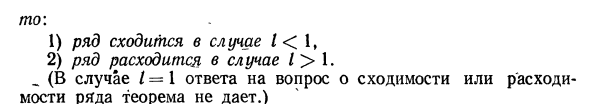



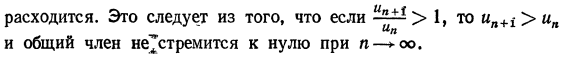
24) Признак Коши (Радикальный)
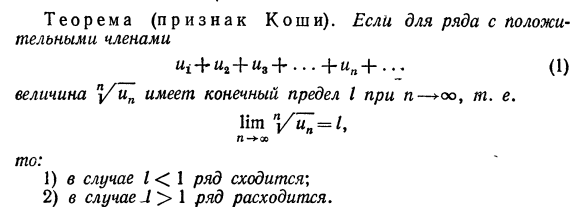

25) Признак Коши (интегральный)
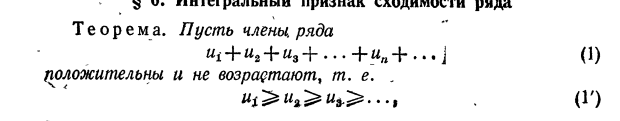

![]()
26) Признак сравнения первого рода

27) Знакочередующиеся ряды. Теорема Лейбница
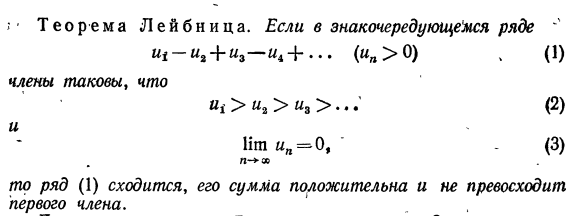



28) Знакопеременные числовые ряды. Достаточное условие сходимости числового ряда
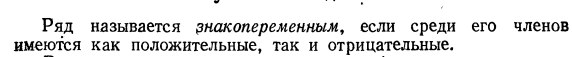
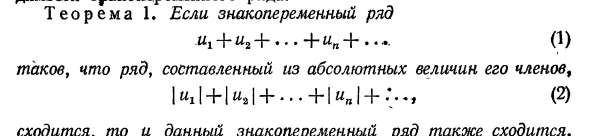

29) Абсолютная и условная сходимости знакопеременных рядов
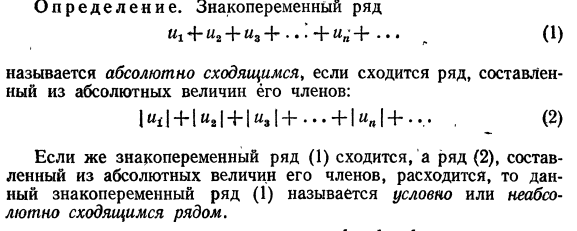

30) Функциональные ряды
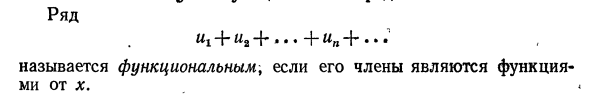
![]()
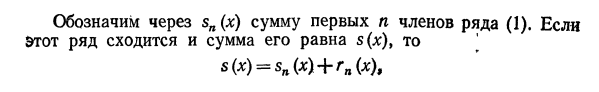

31) Мажорируемые ряды


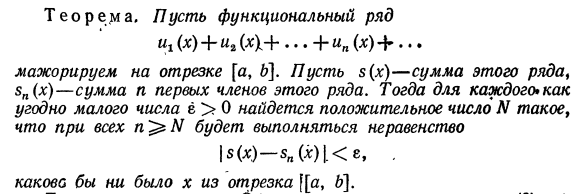


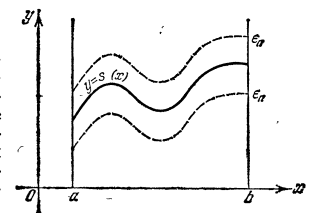

32) Интегрирование и дифференцирование рядов
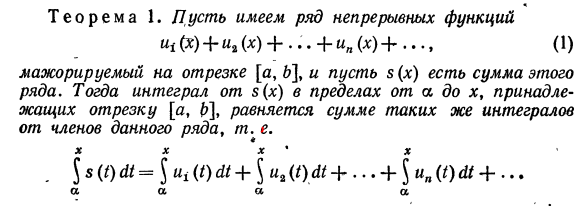
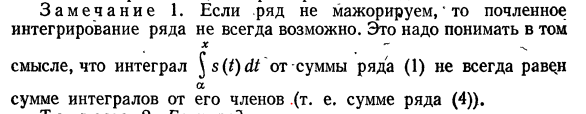


33) Степенные ряды. Теорема Абеля
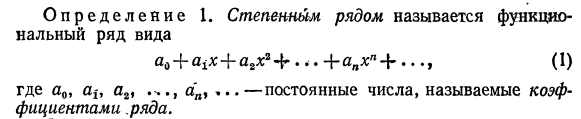



34) Интервал сходимости степенного ряда
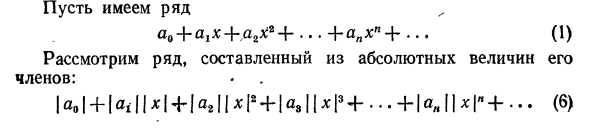



35) Ряды Тейлора и Маклорена


36) Разложение основных элементарных функций в ряды Тейлора и Маклорена

37) Приложение степенных рядов. Биноминальный ряд

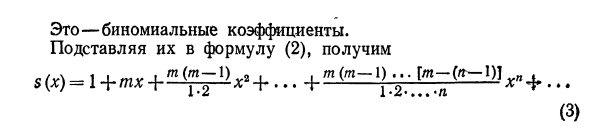
38) Применение степенных рядов. Вычисление определённых интегралов и логарифмов


39) Применение теории полей для решения диффур. Метод итераций
 40)
40)
40) Применение теории полей для решения диффур. Метод последовательного дифференцирования
40)

41) Применение теории полей для решения диффур. Способ неопределенных коэффициентов

42) Ряды Фурье. (основные определения, постановка задач)

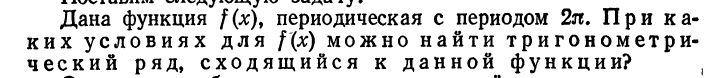
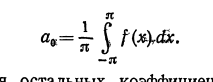
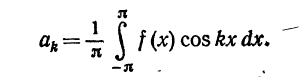



43) Пример разложения функции в ряд Фурье


44) Ряды Фурье для чётных и нечётных функций



45) Ряды Фурье для функций с периодом 2l


