Министерство науки и образования Российской Федерации

ФГБОУ ВО Ивановский государственный химико-технологический университет

Кафедра высшей и прикладной математики

Лабораторная работа

По дисциплине: «Численные методы»

Вариант №19

Выполнил: ст. гр. 2/61 АТП и П П.А. Хавари

Проверил: доц. С.В. Кулакова

Иваново 2017

ЗАДАЧА № 1

Найти решение системы методом простой итерации с точностью 0,0001.

А = В =

Краткая теоретическая часть

Метод простых итераций. (Метод последовательных приближений).

Пусть дана система n линейных уравнений с n неизвестными:

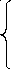
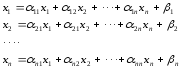(1)

или где - заданные числа; .

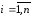
Задаются произвольно n-чисел – нулевое приближение искомой функции.

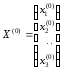
Далее подставляем в правую часть системы (1) нулевое приближение и

находим первое приближение.

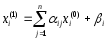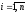, (2)

Затем по 1-ому приближению находят 2-ое, 3-е и т.д.

В результате для k-ого приближения получаем формулу:

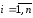, (2’)

Таким образом мы получили последовательность векторов

Х⁽⁰⁾,Х⁽¹⁾,…, Х^(К), к=1,2,…

Если любая из таких последовательностей {Х_i^(к)} сходится некоторому пределу 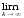x_i^k = c_i ,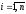 ,то данный вектор с_i, является решением сист. (1)

В равенстве (2’) перейдем к пределу при k→∞ при замене х_i на с_i.

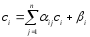
Теорема (достаточные условия сходимости простой итерации):

Пусть выполняется хотя бы одно из следующих условий (нормы матрицы):

а) Если максимум суммы модулей коэффициентов при неизвестных (по строкам) меньше 1:

б) Если максимум суммы модулей коэффициентов при неизвестных (по столбцам) меньше 1:

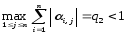
в) Если сумма всех элементов в квадрате меньше 1.

Если выполняется хотя бы одно, тогда справедливы утверждения:

1. система (1) имеет единственное решение (С₁,... С_n);

2. последовательность 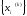, где i = 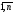определяется по формуле (2), при любом начальном приближении 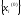сходится к соответствующим компонентам точного решения. i =

3. для приближенного равенства верны оценки (x₁^(k),…x_n^(k))(C_1,…C_n),

а’) если выполняется условие а), то

,

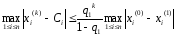б’) если выполняется условие б), то

,

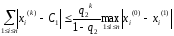в’) если выполняется условие в), то

.

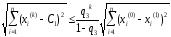Решение:

Найти решение системы методом Зейделя с точностью 0,0001.

А = В =

Представим систему в матричной форме АХ=В

Выразим из СЛАУ х_n:

Проверим, сходится ли система:

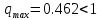
Система сходится, значит можно применять метод простых итераций.

Последовательно вычисляем:

При k=1

Х₁¹ = -0,399*(-1,60963) + 0,0625*0,45957 + 1,019231 = 1,690195

Х₂¹ = -0,06952*1,01923 + 0,25134*0,45957 – 1,6096 = -1,61159

Х₃¹ = 0,01702*1,01923 – 0,05532*(-1,60963) + 0,45957 = 0,57749

Проверим эмпирическое условие окончания итерационного процесса:

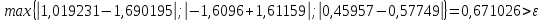
При k=2

Х₁¹ = -0,399*(-1,61159) + 0,0625*0,57749 + 1,019231 = 1,69835

Х₂¹ = -0,06952*1,690195 + 0,25134*0,57749 – 1,6096 = -1,58252

Х₃¹ = 0,01702*1,690195 – 0,05532*(-1,61159) + 0,45957 = 0,57602

Проверим эмпирическое условие окончания итерационного процесса:

Так как они все больше заданного числа 0,0001, продолжаем итерации до тех пор, пока значения не будут меньше 0,0001.

i	x1	x2	x3	ε
0	1,019231	-1,60963	0,459574
1	1,690257	-1,56497	0,565966	0,671026
2	1,679088	-1,58488	0,574918	0,019909
3	1,687592	-1,58186	0,575829	0,008504
4	1,686441	-1,58222	0,575806	0,001151
5	1,686584	-1,58214	0,575807	0,000143

Найдем точное решение:

Высчитываем погрешность:

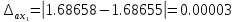
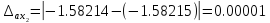
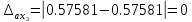
Ответ: Х^*=

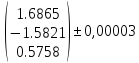
Задание №2:

Для функции, заданной таблично, построить полиномы Ньютона и Лагранжа. Вычислить y(х^* ), y(х^** ).

Определить погрешность. Х^* =Х₀ +0,05. Х^** =Х₅ - 0,15.

i	0	1	2	3	4	5
x	1,2	1,3	1,4	1,5	1,6	1,7
y	4,018	4,025	4,035	4,048	4,012	4,028