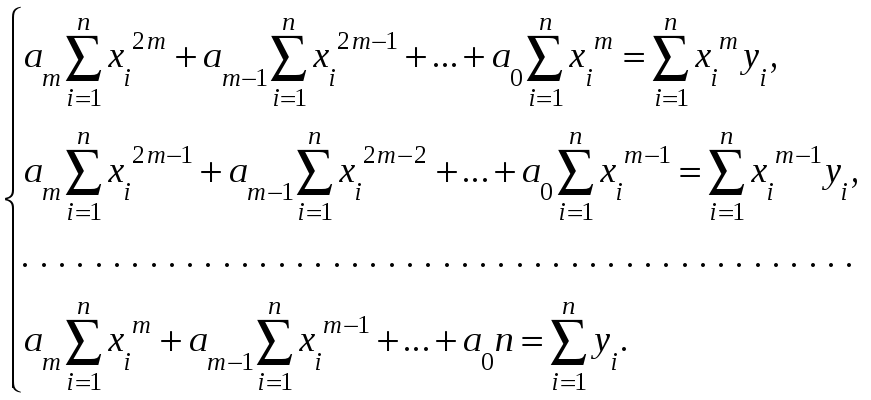- •Лекция 1 Приближённые методы решения слау
- •В) Метод Гаусса. (Метод последовательного исключения переменных)
- •Прямой ход.
- •Формулы прямого хода
- •Обратный ход
- •Формулы обратного хода.
- •Интерполяция, аппроксимация.
- •Оценка погрешности:
- •Приближённое интегрирование функций
- •1) Интегрирование по методу прямоугольников.
- •2) Интегрирование по методу трапеций.
- •3) Интегрирование по методу Симпсона.
- •2.1) Отделение корней.
- •Уточнение корней до заданной точности.
- •1) Метод половинного деления (дихотомии).
- •2) Метод хорд.
- •2) Метод Ньютона (касательных).
- •4) Комбинированный метод (хорд и касательных).
- •Постановка задачи.
- •1Ый усовершенствованный метод Эйлера.
- •2Oй усовершенствованный метод Эйлера.
- •С.) Метод Рунге-Кутта. (4го порядка)
- •D). Метод Рунге–Кутта 3-го порядка
- •Многошаговые методы.
Оценка погрешности:
![]() ;
-n
≤ t
≤ 0; x
є [x0;xn],
μ=max│f(n+1)(x)│
;
-n
≤ t
≤ 0; x
є [x0;xn],
μ=max│f(n+1)(x)│
С.) «МЕТОД НАИМЕНЬШИХ КВАДРАТОВ»
Перечислим особенности, на которые надо обратить внимание при выполнении задания по этой теме.
Предполагается,
что функция
![]() задана в виде таблицы конечного числа
точек
задана в виде таблицы конечного числа
точек
|
хi |
х0 |
х1 |
… |
хn |
, |
|
уi |
y0 |
y1 |
… |
yn |
например, получена экспериментально, где xi, yi (i=1,…,n) – произвольные числа. При этом все
числа xi различны.
Пусть
также имеется некоторая функция
![]() ,
определенная для всех значений xi
(i=1,…,n).
,
определенная для всех значений xi
(i=1,…,n).
Определение 3. Число Т, где
|
|
(7) |
называется
среднеквадратичным
(или среднеквадратическим) уклонением
функции
![]() от заданной
от заданной
![]() .
.
Наряду с числом Т вводят также вспомогательную величину
|
|
(8) |
Функцию
![]() стараются подобрать, чтобы число Т
получилось достаточно малым.
стараются подобрать, чтобы число Т
получилось достаточно малым.
Можно
предложить следующие способы выбора
функции
![]() .
.
Способ
1.
![]() ,
(9)
,
(9)
т.е.
![]() - многочлен степени m,
при этом m<n.
- многочлен степени m,
при этом m<n.
Способ
2.
![]() ,
здесь
,
здесь
![]() - сплайн, т.е. кусочно-полиномиальная
гладкая функция.
- сплайн, т.е. кусочно-полиномиальная
гладкая функция.
Способ
3.
 , (10)
, (10)
т.е.
![]() - частичная сумма ряда Фурье, при этом
m
– четно и m<n.
- частичная сумма ряда Фурье, при этом
m
– четно и m<n.
Перечисленные
способы 1-3 задают для
![]() вид приближающей функции
вид приближающей функции
![]() ,
которая, в свою очередь, зависит от
коэффициентов (или параметров) ai.
Лучшим набором коэффициентов ai
считается тот, для которого величина w
из (8) меньше.
,
которая, в свою очередь, зависит от
коэффициентов (или параметров) ai.
Лучшим набором коэффициентов ai
считается тот, для которого величина w
из (8) меньше.
Определение
4. Говорят,
что функция
![]() найдена для
найдена для
![]() по методу наименьших квадратов (МНК),
если она дает минимально возможное
значение величины w
в соотношении (8).
по методу наименьших квадратов (МНК),
если она дает минимально возможное
значение величины w
в соотношении (8).
Примечание.
Заметим, что при m=n-1
многочлен
![]() ,
полученный по МНК, совпадает с
интерполяционным многочленом и,
следовательно, соответствующее
среднеквадратичное уклонение
(теоретически) равно числу
,
полученный по МНК, совпадает с
интерполяционным многочленом и,
следовательно, соответствующее
среднеквадратичное уклонение
(теоретически) равно числу
![]() .
При использовании в расчетах ЭВМ это
уклонение, как правило, получается
числом, отличным от нуля.
.
При использовании в расчетах ЭВМ это
уклонение, как правило, получается
числом, отличным от нуля.
Рассмотрим
в качестве приближающей функции многочлен
степени m,
который имеет вид
![]()
Согласно
методу наименьших квадратов наилучшими
коэффициентами
![]() считаются те, для которых сумма квадратов
уклонений будет минимальной, т. е.
считаются те, для которых сумма квадратов
уклонений будет минимальной, т. е.
|
|
|
|
Т
есть функция коэффициентов
![]() .
Наряду с функцией Т
рассматривают функцию S
вида:
.
Наряду с функцией Т
рассматривают функцию S
вида:
|
|
|
|
Очевидно, что S и Т достигают своего минимума в одной точке. Далее для отыскания точки минимума будем рассматривать функцию S, поскольку она удобнее для вычислений.
При данной приближающей функции критерий близости, который используется в методе наименьших квадратов, запишется следующим образом:
|
|
|
(11) |
|
|
|
|
Используя
необходимое условие экстремума функции
нескольких переменных, получим систему
для определения коэффициентов
![]() ,
где
,
где
![]() :
:
|
|
|
(12) |
То есть:
|
|
|
(13) |
Лекция 3